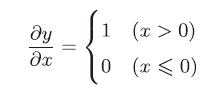深度学习入门(四):误差反向传播
本文为《深度学习入门 基于Python的理论与实现》的部分读书笔记
代码以及图片均参考此书
目录
- 计算图
- 用计算图求解
- 局部计算
- 反向传播
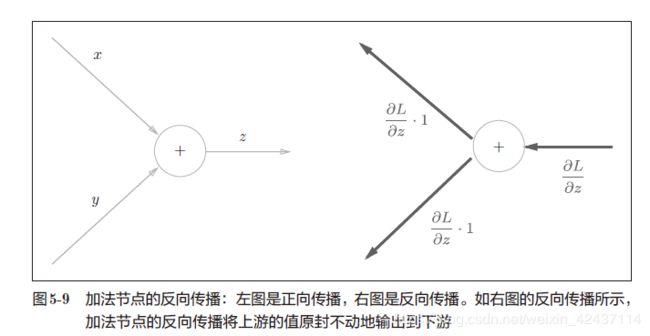
- 加法节点的反向传播
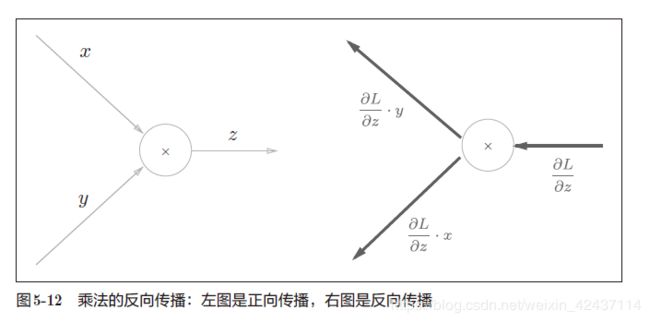
- 乘法节点的反向传播
- 链式法则与计算图
- 通过计算图进行反向传播
- 激活函数层的实现
- Relu层
- Sigmoid层
- Affine/Softmax层的实现
- Affine层
- Softmax-with-loss(cross enrtopy loss)层
- 正向传播
- 反向传播
- 梯度确认(gradient check)
- 通过组装各个层重新实现二层神经网络
计算图
用计算图求解
局部计算
- 计算图的特征是可以通过传递“局部计算”获得最终结果。换言之,各个节点处只需进行与自己有关的计算,不用考虑全局。
反向传播
加法节点的反向传播
乘法节点的反向传播
- 乘法的反向传播需要正向传播时的输入信号值。因此,实现乘法节点的反向传播时,要保存正向传播的输入信号
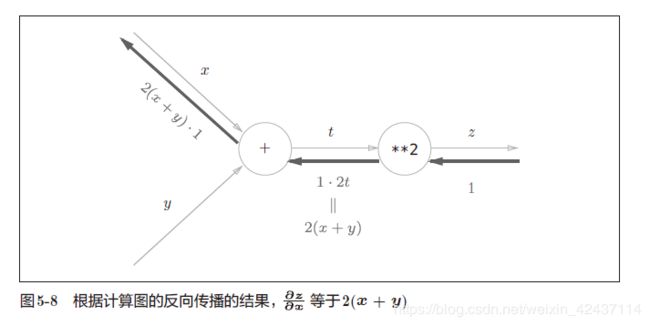
链式法则与计算图
通过计算图进行反向传播
-
使用计算图最大的原因是,可以通过反向传播高效计算导数。
-
例:求问题一中“支付金额关于苹果的价格的导数“

如图5-5 所示,反向传播使用与正方向相反的箭头(粗线)表示。反向传播传递“局部导数”,将导数的值写在箭头的下方。从这个结果中可知,“支付金额关于苹果的价格的导数”的值是2.2。
激活函数层的实现
Relu层
import numpy as np
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = x < 0
x[self.mask] = 0
return x
def backward(self, dout):
dout[self.mask] = 0
return dout
if __name__ == "__main__":
layer = Relu()
x = np.random.randn(3, 3)
print('x:', x, sep='\n')
save = x.copy()
out = layer.forward(save)
print('out:', out, sep='\n')
dout = layer.backward(np.ones_like(save))
print('dout:', dout, sep='\n')
代码输出:
x:
[[ 0.08621289 1.20328454 1.81030439]
[-1.31113673 -0.11453987 0.88408891]
[ 0.14068574 -0.479992 -1.73015689]]
out:
[[0.08621289 1.20328454 1.81030439]
[0. 0. 0.88408891]
[0.14068574 0. 0. ]]
dout:
[[1. 1. 1.]
[0. 0. 1.]
[1. 0. 0.]]
Sigmoid层
- 因此,Sigmoid 层的反向传播,只根据正向传播的输出就能计算出来。
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out.copy()
return out
def backward(self, dout):
return dout * self.out * (1 - self.out)
Affine/Softmax层的实现
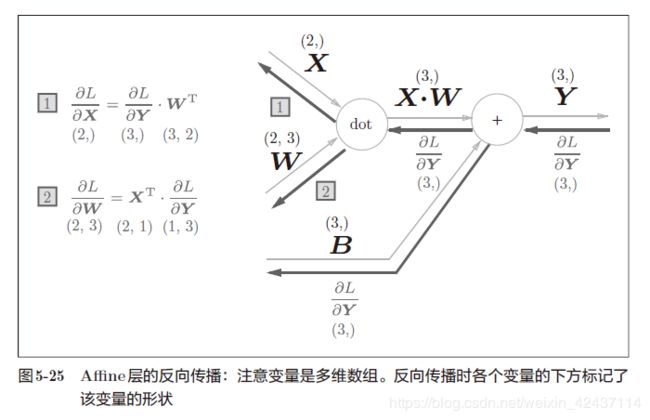
Affine层
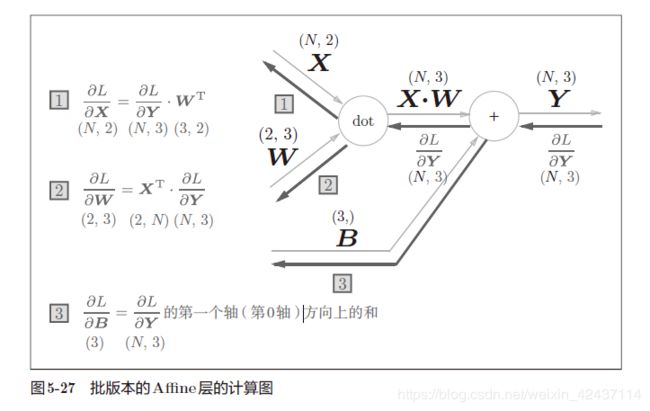
- 设批处理的样本数量为 N N N,上一层神经元数量为 a a a,本层神经元数量为 b b b
X X X为输入, W W W为本层权重, B B B为本层偏置, Y Y Y= X ⋅ W + B X\cdot W + B X⋅W+B
x i j x_{ij} xij表示第i个样本的第j个输入
w i j w_{ij} wij表示前一层第i个神经元与后一层第j个神经元连接的权重
y i j y_{ij} yij表示第i个样本的第j个输出
b i b_{i} bi表示第i个神经元的偏置
∂ L ∂ w i j = ∑ k = 1 N ∂ L ∂ y k j ∗ ∂ y k j ∂ w i j = ∑ k = 1 N ∂ L ∂ y k j ∗ ∂ ( ∑ m = 1 a ( x k m ∗ w m j ) + b j ) ∂ w i j = ∑ k = 1 N ∂ L ∂ y k j ∗ x k i ∴ ∂ L ∂ W = X T ⋅ ∂ L ∂ Y \begin{aligned} \frac{\partial L}{\partial w_{ij}} &= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{kj}} * \frac{\partial y_{kj}}{\partial w_{ij}} \\&= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{kj}} * \frac{\partial (\sum_{m=1}^{a} (x_{km} * w_{mj}) + b_{j})}{\partial w_{ij}} \\&= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{kj}} * x_{ki} \\ \therefore \frac{\partial L}{\partial W} &= X^T \cdot \frac{\partial L}{\partial Y} \end{aligned} ∂wij∂L∴∂W∂L=k=1∑N∂ykj∂L∗∂wij∂ykj=k=1∑N∂ykj∂L∗∂wij∂(∑m=1a(xkm∗wmj)+bj)=k=1∑N∂ykj∂L∗xki=XT⋅∂Y∂L
∂ L ∂ x i j = ∑ k = 1 b ∂ L ∂ y i k ∗ ∂ y i k ∂ x i j = ∑ k = 1 b ∂ L ∂ y i k ∗ ∂ ( ∑ m = 1 a ( x i m ∗ w m k ) + b k ) ∂ x i j = ∑ k = 1 b ∂ L ∂ y i k ∗ w j k ∴ ∂ L ∂ X = ∂ L ∂ Y ⋅ W T \begin{aligned} \frac{\partial L}{\partial x_{ij}} &= \sum_{k=1}^{b} \frac{\partial L}{\partial y_{ik}} * \frac{\partial y_{ik}}{\partial x_{ij}} \\&= \sum_{k=1}^{b} \frac{\partial L}{\partial y_{ik}} * \frac{\partial (\sum_{m=1}^{a} (x_{im} * w_{mk}) + b_{k})}{\partial x_{ij}} \\&= \sum_{k=1}^{b} \frac{\partial L}{\partial y_{ik}} * w_{jk} \\ \therefore \frac{\partial L}{\partial X} &= \frac{\partial L}{\partial Y} \cdot W^T \end{aligned} ∂xij∂L∴∂X∂L=k=1∑b∂yik∂L∗∂xij∂yik=k=1∑b∂yik∂L∗∂xij∂(∑m=1a(xim∗wmk)+bk)=k=1∑b∂yik∂L∗wjk=∂Y∂L⋅WT
∂ L ∂ b i = ∑ k = 1 N ∂ L ∂ y k i ∗ ∂ y k i ∂ b i = ∑ k = 1 N ∂ L ∂ y k i ∗ ∂ ( ∑ m = 1 a ( x k m ∗ w m i ) + b i ) ∂ b i = ∑ k = 1 N ∂ L ∂ y k i ∴ ∂ L ∂ B = ∂ L ∂ Y 的 第 0 轴 上 的 和 \begin{aligned} \frac{\partial L}{\partial b_{i}} &= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{ki}} * \frac{\partial y_{ki}}{\partial b_{i}} \\&= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{ki}} * \frac{\partial (\sum_{m=1}^{a} (x_{km} * w_{mi}) + b_{i})}{\partial b_{i}} \\&= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{ki}} \\ \therefore \frac{\partial L}{\partial B} &= \frac{\partial L}{\partial Y} 的第0轴上的和 \end{aligned} ∂bi∂L∴∂B∂L=k=1∑N∂yki∂L∗∂bi∂yki=k=1∑N∂yki∂L∗∂bi∂(∑m=1a(xkm∗wmi)+bi)=k=1∑N∂yki∂L=∂Y∂L的第0轴上的和
class Affine:
def __init__(self, w, b):
self.w = w
self.b = b
def forward(self, x):
# 对应张量要reshape为二维矩阵进行全连接层计算
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
return np.dot(self.x, self.w) + self.b
def backward(self, dout):
self.dw = np.dot(self.x.T, dout)
self.db = dout if dout.ndim == 1 else np.sum(dout, axis=0)
return np.dot(dout, self.w.T).reshape(*self.original_x_shape) # 还原输入数据的形状(对应张量) # dx
Softmax-with-loss(cross enrtopy loss)层
正向传播
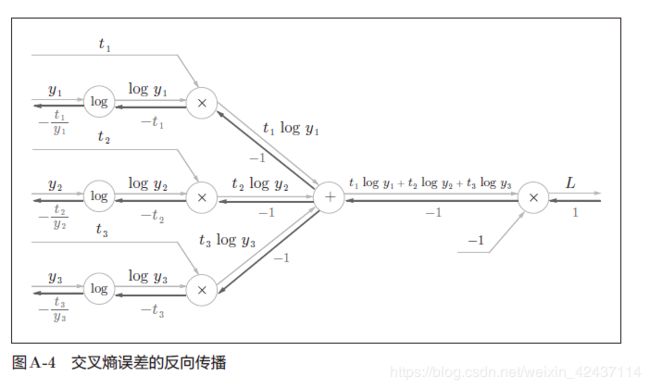
反向传播
-
正向传播时若有分支流出,则反向传播时它们的反向传播的值会相加。
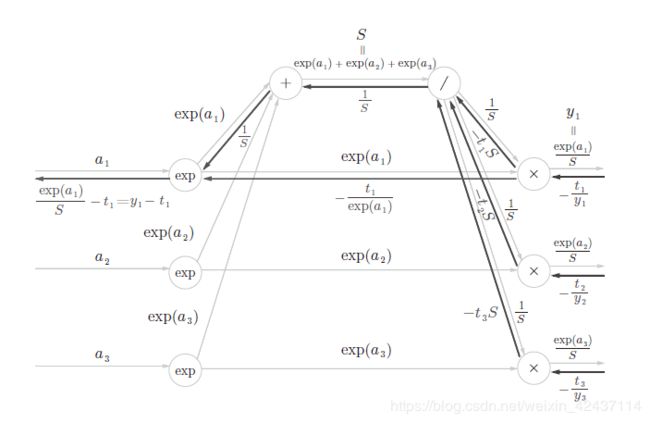
以右上角的 “/” 结点为例:
∂ L ∂ S = ∂ L ∂ y 1 ∗ ∂ y 1 ∂ 1 S ∗ ∂ 1 S ∂ S + ∂ L ∂ y 2 ∗ ∂ y 2 ∂ 1 S ∗ ∂ 1 S ∂ S + ∂ L ∂ y 3 ∗ ∂ y 3 ∂ 1 S ∗ ∂ 1 S ∂ S \frac{\partial L}{\partial S} = \frac{\partial L}{\partial y_1} * \frac{\partial y_1}{\partial \frac{1}{S} } * \frac{\partial \frac{1}{S}}{\partial S} + \frac{\partial L}{\partial y_2} * \frac{\partial y_2}{\partial \frac{1}{S} } * \frac{\partial \frac{1}{S}}{\partial S} + \frac{\partial L}{\partial y_3} * \frac{\partial y_3}{\partial \frac{1}{S} } * \frac{\partial \frac{1}{S}}{\partial S} ∂S∂L=∂y1∂L∗∂S1∂y1∗∂S∂S1+∂y2∂L∗∂S1∂y2∗∂S∂S1+∂y3∂L∗∂S1∂y3∗∂S∂S1
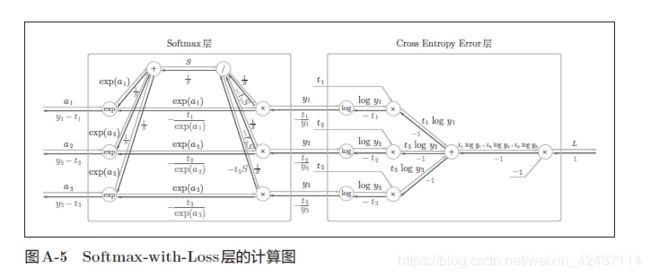
不使用计算图进行推导:
为了推理上方便书写,先引入克罗内克符号:
δ i , j = 1 i f i = j \delta_{i,j} = 1 \ \ \ \ \ \ \ \ \ \ \ \ \ if \ i = j δi,j=1 if i=j δ i , j = 0 i f i ≠ j \delta_{i,j} = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ if \ i \neq j δi,j=0 if i=j
下面正式进行推导:
设 S = ∑ m e a m , 则 y p = e a p S \begin{aligned} 设S=\sum_m e^{a_m} , 则y_p = \frac {e^{a_p}}{S} \end{aligned} 设S=m∑eam,则yp=Seap ∂ L ∂ y p = − t k y k \begin{aligned} \frac {\partial L}{\partial y_p} &= -\frac{t_k}{y_k} \end{aligned} ∂yp∂L=−yktk ∴ ∂ L ∂ a k = ∑ p ∂ L ∂ y p ∂ y p ∂ a k = ∑ p − t p y p S e a p δ p k − e a p ∂ S ∂ a k S 2 \begin{aligned} \therefore \frac {\partial L}{\partial a_k} &= \sum_p \frac {\partial L}{\partial y_p} \frac {\partial y_p}{\partial a_k} \\&= \sum_p -\frac{t_p}{y_p} \frac{Se^{a_p}\delta _{pk} - {e^{a_p}} \frac {\partial S}{\partial a_k} }{S^2} \end{aligned} ∴∂ak∂L=p∑∂yp∂L∂ak∂yp=p∑−yptpS2Seapδpk−eap∂ak∂S ∵ ∂ S ∂ a k = ∂ ∑ m e a m ∂ a k = e a k \begin{aligned} \because \frac {\partial S}{\partial a_k} &= \frac {\partial \sum_m e^{a_m}}{\partial a_k} \\&= e^{a_k} \end{aligned} ∵∂ak∂S=∂ak∂∑meam=eak ∴ ∂ L ∂ a k = ∑ p − t p e a p S e a p δ p k − e a p e a k S = ∑ p − t p e a p ( e a p δ p k − e a p e a k S ) = ∑ p − t p δ p k + t p e a k S = − t k + ∑ p t p y k = − t k + y k \begin{aligned} \therefore \frac {\partial L}{\partial a_k} &= \sum_p -\frac{t_p}{e^{a_p}} \frac{Se^{a_p}\delta _{pk} - e^{a_p} e^{a_k} }{S} \\&=\sum_p -\frac{t_p}{e^{a_p}} (e^{a_p}\delta _{pk} - \frac {e^{a_p} e^{a_k}}{S} ) \\&= \sum_p -t_p \delta_{pk} + \frac {t_p e^{a_k}}{S} \\&= -t_k + \sum_p t_py_k \\&= -t_k + y_k \end{aligned} ∴∂ak∂L=p∑−eaptpSSeapδpk−eapeak=p∑−eaptp(eapδpk−Seapeak)=p∑−tpδpk+Stpeak=−tk+p∑tpyk=−tk+yk -
使用交叉熵误差作为softmax函数的损失函数后,反向传播得到(y1 − t1, y2 − t2, y3 − t3)这样“ 漂亮”的结果。实际上,这样“漂亮”的结果并不是偶然的,而是为了得到这样的结果,特意设计了交叉熵误差函数。回归问题中输出层使用“恒等函数”,损失函数使用“平方和误差”,也是出于同样的理由。也就是说,使用“平方和误差”作为“恒等函数”的损失函数,反向传播才能得到(y1 −t1, y2 − t2, y3 − t3)这样“漂亮”的结果。
class SoftmaxWithLoss:
def __init__(self):
pass
def forward(self, x, t):
self.t = t.copy()
self.y = softmax(x)
return cross_entropy_error(self.y, t)
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况
dx = self.y - self.t
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
# 书上写的是这里除以batch_size后,传递给前面的层的是单个数据的误差
# 我的理解是与前面全连接层的导数计算有关
return dx / batch_size
最后将导数除以batch_size,我的理解是与前面全连接层的导数计算有关
-
∂ L ∂ w i j = ∑ k = 1 N ∂ L ∂ y k j ∗ ∂ y k j ∂ w i j = ∑ k = 1 N ∂ L ∂ y k j ∗ ∂ ( ∑ m = 1 a ( x k m ∗ w m j ) + b j ) ∂ w i j = ∑ k = 1 N ∂ L ∂ y k j ∗ x k i \frac{\partial L}{\partial w_{ij}} \\= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{kj}} * \frac{\partial y_{kj}}{\partial w_{ij}} \\= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{kj}} * \frac{\partial (\sum_{m=1}^{a} (x_{km} * w_{mj}) + b_{j})}{\partial w_{ij}} \\= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{kj}} * x_{ki} ∂wij∂L=∑k=1N∂ykj∂L∗∂wij∂ykj=∑k=1N∂ykj∂L∗∂wij∂(∑m=1a(xkm∗wmj)+bj)=∑k=1N∂ykj∂L∗xki
-
∂ L ∂ b i = ∑ k = 1 N ∂ L ∂ y k i ∗ ∂ y k i ∂ b i = ∑ k = 1 N ∂ L ∂ y k i ∗ ∂ ( ∑ m = 1 a ( x k m ∗ w m i ) + b i ) ∂ b i = ∑ k = 1 N ∂ L ∂ y k i \frac{\partial L}{\partial b_{i}} \\= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{ki}} * \frac{\partial y_{ki}}{\partial b_{i}} \\= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{ki}} * \frac{\partial (\sum_{m=1}^{a} (x_{km} * w_{mi}) + b_{i})}{\partial b_{i}} \\= \sum_{k=1}^{N} \frac{\partial L}{\partial y_{ki}} ∂bi∂L=∑k=1N∂yki∂L∗∂bi∂yki=∑k=1N∂yki∂L∗∂bi∂(∑m=1a(xkm∗wmi)+bi)=∑k=1N∂yki∂L
如上所示batch_size越大(即N越大),则损失函数值对每一个权重或偏置的偏导数也就越大,这是不对的,因此需要将 ∂ L ∂ Y \frac{\partial L}{\partial Y} ∂Y∂L除以N
- 由此可以看出损失函数求得的导数 ∂ L ∂ Y \frac{\partial L}{\partial Y} ∂Y∂L都应该除以batch_size!
梯度确认(gradient check)
- 数值微分的优点是实现简单,因此,一般情况下不太容易出错。而误差反向传播法的实现很复杂,容易出错。所以,经常会比较数值微分的结果和误差反向传播法的结果,以确认误差反向传播法的实现是否正确。
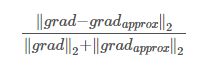
- 通过矩阵的欧几里得范数来判断,分母使得该式成比例,不会太大也不会太小
- Doesn’t work with dropout(dropout随机删去一些神经元,使得损失函数L难以计算)
- Run at random initialization perhaps again after some training(有可能(极小的可能性)w和b只有在接近于0的时候梯度确认是正常的,但训练一段时间后w和b远离0后反向传播计算的梯度就不正常了,因此可以在网络训练一段时间之后再进行梯度确认)
- 当计算值比较大时,应逐一比较数值微分计算的梯度与反向传播计算的梯度中的每一项,看看是哪一个参数的梯度计算出了问题
def gradient_check(net, x_batch, t_batch):
grad_numerical = net.numerical_gradient(x_batch, t_batch)
grad_backprop = net.gradient(x_batch, t_batch)
for key in grad_numerical.keys():
print(key, ':')
diff1 = np.mean(np.abs(grad_numerical[key] - grad_backprop[key]))
print('diff1:', diff1)
# diff2 = 1e-7 -> correct
# diff2 > 1e-5 -> please check again!
# diff2 > 1e-3 -> concerned
diff2 = np.linalg.norm(grad_numerical[key] - grad_backprop[key], 2) / (np.linalg.norm(grad_numerical[key], 2) + np.linalg.norm(grad_backprop[key], 2))
print('diff2:', diff2)
- 这里diff1的实现是使用的本书中的方法
- diff2的实现是通过计算矩阵的欧几里得范数,判断的标准写在了上面代码的注释里
通过组装各个层重新实现二层神经网络
import sys
file_path = __file__.replace('\\', '/')
dir_path = file_path[: file_path.rfind('/')] # 当前文件夹的路径
pardir_path = dir_path[: dir_path.rfind('/')]
sys.path.append(pardir_path) # 添加上上级目录到python模块搜索路径
import numpy as np
from func.gradient import numerical_gradient, gradient_check
from layer.activation import Relu, Affine, SoftmaxWithLoss, Sigmoid
import matplotlib.pyplot as plt
from collections import OrderedDict
class TwoLayerNet:
"""
2 Fully Connected layers
softmax with cross entropy error
"""
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
self.params = {}
self.params['w1'] = np.random.randn(input_size, hidden_size) * weight_init_std
self.params['b1'] = np.zeros(hidden_size)
self.params['w2'] = np.random.randn(hidden_size, output_size) * weight_init_std
self.params['b2'] = np.zeros(output_size)
self.layers = OrderedDict()
self.layers['affine1'] = Affine(self.params['w1'], self.params['b1'])
self.layers['relu1'] = Relu()
self.layers['affine2'] = Affine(self.params['w2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = y.argmax(axis=1)
if t.ndim != 1:
t = t.argmax(axis=1)
accuracy = np.sum(y == t) / x.shape[0]
return accuracy
def numerical_gradient(self, x, t):
loss = lambda w: self.loss(x, t)
grads = {}
grads['w1'] = numerical_gradient(loss, self.params['w1'])
grads['b1'] = numerical_gradient(loss, self.params['b1'])
grads['w2'] = numerical_gradient(loss, self.params['w2'])
grads['b2'] = numerical_gradient(loss, self.params['b2'])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
for layer_name in reversed(self.layers):
dout = self.layers[layer_name].backward(dout)
grads = {}
grads['w1'] = self.layers['affine1'].dw
grads['b1'] = self.layers['affine1'].db
grads['w2'] = self.layers['affine2'].dw
grads['b2'] = self.layers['affine2'].db
return grads
if __name__ == '__main__':
from dataset.mnist import load_mnist
import pickle
import os
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=True)
# hyper parameters
lr = 0.1
batch_size = 100
iters_num = 10000
# setting
train_flag = 0 # 进行训练还是预测
pretrain_flag = 0 # 加载上一次训练的参数
gradcheck_flag = 1 # 对已训练的网络进行梯度检验
pkl_file_name = dir_path + '/two_layer_net.pkl'
train_size = x_train.shape[0]
train_loss_list = []
train_acc_list = []
test_acc_list = []
best_acc = 0
iter_per_epoch = max(int(train_size / batch_size), 1)
net = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
if (pretrain_flag == 1 or train_flag == 0) and os.path.exists(pkl_file_name):
with open(pkl_file_name, 'rb') as f:
net = pickle.load(f)
print('params loaded!')
if train_flag == 1:
print('start training!')
for i in range(iters_num):
# 选出mini-batch
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
# grads_numerical = net.numerical_gradient(x_batch, t_batch)
grads = net.gradient(x_batch, t_batch)
# 更新参数
for key in ('w1', 'b1', 'w2', 'b2'):
net.params[key] -= lr * grads[key]
train_loss_list.append(net.loss(x_batch, t_batch))
# 记录学习过程
if i % iter_per_epoch == 0:
train_acc_list.append(net.accuracy(x_train, t_train))
test_acc_list.append(net.accuracy(x_test, t_test))
print("train acc, test acc | ", train_acc_list[-1], ", ", test_acc_list[-1])
if test_acc_list[-1] > best_acc:
best_acc = test_acc_list[-1]
with open(pkl_file_name, 'wb') as f:
pickle.dump(net, f)
print('net params saved!')
# 绘制图形
fig, axis = plt.subplots(1, 1)
x = np.arange(len(train_acc_list))
axis.plot(x, train_acc_list, 'r', label='train acc')
axis.plot(x, test_acc_list, 'g--', label='test acc')
markers = {'train': 'o', 'test': 's'}
axis.set_xlabel("epochs")
axis.set_ylabel("accuracy")
axis.set_ylim(0, 1.0)
axis.legend(loc='best')
plt.show()
else:
if gradcheck_flag == 1:
gradient_check(net, x_train[:3], t_train[:3])
print(net.accuracy(x_train[:], t_train[:]))
先进行梯度确认,设置gradcheck_flag=1,train_flag=0
代码输出如下
w1 :
diff1: 2.6115099710177576e-11
diff2: 5.083025533280819e-08
b1 :
diff1: 2.2425837345792317e-10
diff2: 5.04159103684074e-08
w2 :
diff1: 1.3242105311984443e-10
diff2: 4.724560085528282e-08
b2 :
diff1: 2.712055815786953e-10
diff2: 5.095936065001308e-08
看起来反向传播计算得到的梯度应该是正确的
那么下面就正式进入网络训练吧,设置train_flag=1
代码输出:
start training!
train acc, test acc | 0.10571666666666667 , 0.1042
net params saved!
train acc, test acc | 0.9058833333333334 , 0.9077
net params saved!
train acc, test acc | 0.9251666666666667 , 0.9275
net params saved!
train acc, test acc | 0.9367166666666666 , 0.9353
net params saved!
train acc, test acc | 0.9477166666666667 , 0.9447
net params saved!
train acc, test acc | 0.9528833333333333 , 0.9509
net params saved!
train acc, test acc | 0.9583 , 0.9555
net params saved!
train acc, test acc | 0.9610333333333333 , 0.9578
net params saved!
train acc, test acc | 0.9665 , 0.9623
net params saved!
train acc, test acc | 0.9686333333333333 , 0.9647
net params saved!
train acc, test acc | 0.9702333333333333 , 0.9659
net params saved!
train acc, test acc | 0.9720833333333333 , 0.9679
net params saved!
train acc, test acc | 0.9742166666666666 , 0.9671
train acc, test acc | 0.9735666666666667 , 0.9682
net params saved!
train acc, test acc | 0.9770833333333333 , 0.9709
net params saved!
train acc, test acc | 0.9751 , 0.9678
train acc, test acc | 0.9789166666666667 , 0.9717
net params saved!