UCI库中Mines vs. Rocks的数据集属性可视化展示

数据集描述：
从各种不同的纵横角度获得的信号，每个样本有60个从不同地点接收到的仪器测量值（每个模式是一组60个数字，范围为0.0到1.0），最后一个标记岩石（R)和水雷(M)
任务是根据声纳返回的测量信息，进行分类，从而发现未爆炸的水雷。

data_url = "http://archive.ics.uci.edu/ml/machine-learning-databases/undocumented/connectionist-bench/sonar/sonar.all-data"
dataset = pd.read_csv(data_url,prefix='x')   #shape(207, 61)
dataset.head()
dataset.tail()
summary = dataset.describe()
print(summary)

输出：（部分）

在这里可以观察不同分位数之间的差异。对于同意属性，如果存在某一个差异严重异于其他差异，则说明存在异常点。这就值得进一步分析数据。

手段①：平行坐标图 用于多个属性问题的可视化，对于一个二分类问题（本例），横轴对应着每个样本的所有属性，纵轴代表着标签值。
在水平坐标图中，每个样本都对应着一条折线（横轴为每个观测值的对应点，刻度可以是x1,x2,x3,代表变量1，2，3…)
Mines vs. Rocks数据集的水平坐标图：

#这里对不同标签的样本的折线进行了颜色区分。R标签样本为红色折线，蓝色为雷的样本
plt.figure(figsize=(10,6))
for item in range(207):
    if dataset.iat[item,60] == 'R':
        pcolor = 'red'
    else:
        pcolor = 'blue'
    example = dataset.iloc[item,0:60]
    plt.plot(example,color = pcolor)
plt.xlabel('example',fontsize = 20)
plt.xticks([])
plt.ylabel('value',fontsize = 20)
plt.show()

这个图的横轴应该有60个值的，分别对应着60个变量（各个属性值位于0~1之间），用All variables代替

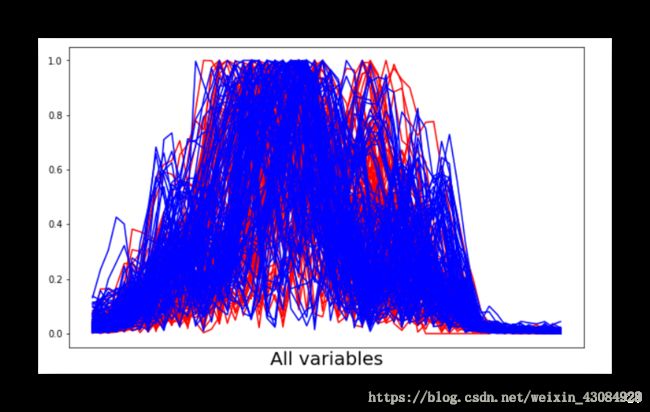
这个数据集并不能很好的区分类别。著名的’鸢尾花数据集‘就可以很明显的区分出不同类别。

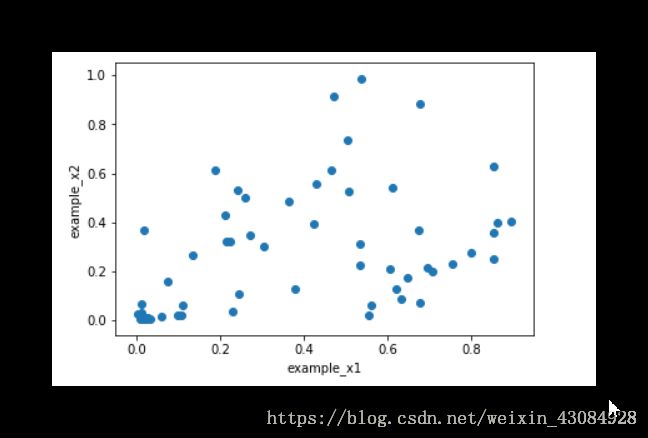
手段②：交会图 可以展示数据间关系的密切程度
Mines vs. Rocks数据集属性对间的交会图

#这里是1号样本数据的属性跟2号样本的属性之间的关系
example1 = dataset.iloc[1,:60]
example2 = dataset.iloc[2,:60]
plt.scatter(example1,example2)
plt.xlabel('example_x1')
plt.ylabel('example_x2')
plt.show()

输出：

#这里是2号样本数据的属性跟30号样本的属性之间的关系
example = dataset.iloc[2,:60]
example30 = dataset.iloc[30,:60]
plt.scatter(example2,example30)
plt.xlabel('example_x2')
plt.ylabel('example_x30')
plt.show()

输出：

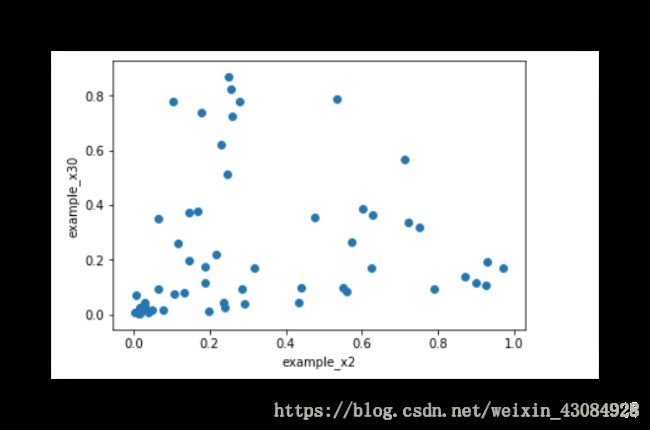
基本上交会图上的点如果聚集在一条’线‘则说明相关性高，相关性不高的交会图上的点可能会扩散一些呈’球形‘
上述例子的小结论：
由于声纳的特性从低频到高频的变化，样本数据依据时间获取的，我们猜想，相隔的样本之间的相关程度可能高于间隔大样本，上面的两个图也证实了我们的猜想，第一个图为样本1，2之间的交会图，相关程度比样本2，30程度来得要高。
应用同样的原则，我们可以画出任意一个指定的变量跟最终目标的交会图，从而得出哪些变量跟最终目标相关程度

分类标签和实数值属性之间的相关性：
这里需要进行一点处理，就是对于标签，M ，R为类别变量，需要进行转化。

#转化代码  1表示标签为岩石，0表示标签为雷
from sklearn.preprocessing import LabelEncoder
LE = LabelEncoder()
target = dataset.iloc[:,60]
target = LE.fit_transform(target)

#取30号变量研究其与最终目标的相关性
x_30 = dataset.iloc[:,30]
plt.figure(figsize=(15,6))
plt.scatter(x_30,target)
plt.xlabel('x_30')
plt.ylabel('label')

输出：

由于是个二分问题，这里取变量30的中值为界，x_30小于0.5，下方数据比较密集，x_30大于0.5，上方数据比较密集。
得出的一点小结论：
这里可以构造一个很粗略的分类器，即：对于x_30小于0.5的样本，我们归类于M，大于0.5归类于R。这样我们可以得到一个略微比随即预测要好的分类器。当然这作为最终结果太烂了。但是，别忘了，我们只取了诸多变量中的一个1/60得到的这个分类器。
                                                                                                                                       未完待续。。。