深度学习笔记（5）：第一课第二周的作业题第一部分详解与代码

前言，

这里笔者使用的是这个网站下的计算资源，感兴趣的同学也可以来fork练练手
https://www.kesci.com/home/project/5dd236a800b0b900365eca9b

HelloWorld任务

熟悉一下平台，没啥好说的
注意两点 1）记住$shift+Enter$快捷键 2）记住要从import那一段代码开始一直运行到你需要的部分，否则可能会因为中断而引起代码错误

手写一个简单的sigmoid函数

很简单，我们只需要知道对于单个的数学公式，python提供了$math.function$系列函数，在这里面，我们使用$math.exp$

# GRADED FUNCTION: basic_sigmoid

import math

def basic_sigmoid(x):
    """
    Compute sigmoid of x.

    Arguments:
    x -- A scalar

    Return:
    s -- sigmoid(x)
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    s=1/(1+math.exp(-x))
    ### END CODE HERE ###
    
    return s

手写整个向量组的sigmoid函数

当我们想要处理数组，向量这种结构的时候。我们就应该想到numpy这一强大的工具。

输入numpy的x可以是实数，向量或矩阵。 我们在numpy中使用的表示向量、矩阵等的数据结构称为numpy数组。

对于这道题，如果我们想要把向量（矩阵中），每一个变量都套上一个sigmoid，我们就要学会用整体的角度思考问题，然后对numpy的系列函数大用特用。

值得注意的是，numpy直接的很多操作都是作用于其中每一个元素而言的。加减乘除以及一系列函数都是如此。
举例说明

import numpy as np

# example of np.exp
x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
print(x+y)
#Output:[5,7,9]
print(2*x)
#Output:[2,4,6]
print(1/x)
#Output:[1,0.5,0.333333]
print(x+1)
#Output:[2,3,4]Using the broadcast formula
print(np.exp(x)) # result is (exp(1), exp(2), exp(3))
#Output：[ 2.71828183  7.3890561  20.08553692]

所以我们可以把我们的sigmoid从这个角度拆解成，对于输入的向量，先计算$a=np.exp(-x)$，再把每一项都加1,$b=a+1$，（运用到广播技术，1被扩展成和向量规模一样的全1向量），再每个取倒数，$c=1/b$
代码如下

# GRADED FUNCTION: sigmoid

import numpy as np # this means you can access numpy functions by writing np.function() instead of numpy.function()

def sigmoid(x):
    """
    Compute the sigmoid of x

    Arguments:
    x -- A scalar or numpy array of any size

    Return:
    s -- sigmoid(x)
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    s= 1/(np.exp(-x)+1)
    ### END CODE HERE ###
    
    return s

手写一个梯度函数

这个也很简单，我们要写sigmoid的梯度函数，只需要知道对于sigmoid函数$a^{\prime }=a(1-a)$，所以进而我们可以得到下列代码

# GRADED FUNCTION: sigmoid_derivative

def sigmoid_derivative(x):
    """
    Compute the gradient (also called the slope or derivative) of the sigmoid function with respect to its input x.
    You can store the output of the sigmoid function into variables and then use it to calculate the gradient.
    
    Arguments:
    x -- A scalar or numpy array

    Return:
    ds -- Your computed gradient.
    """
    
    ### START CODE HERE ### (≈ 2 lines of code)
    s = sigmoid (x)
    ds = s*(1-s)
    ### END CODE HERE ###
    
    return ds

重塑数组规模

这里面要将数组的规模重塑（说白了就是数组要重塑成为“多少×多少×多少…”）在计算机科学中，图像由shape为$(length,height,depth=3)$的3D数组表示。
这里面主要涉及两个函数，1）对于一个np对象x，我们可以使用x.shape[0]/[1]/[2]获取其$length,height,depth$ 2)对于一个numpy变量x，我们可以使用x.reshape将其的规模改变，但是注意一定要使得新规模的各个维度的乘积，与旧规模相等，（也就是说个数一定要对上）。
reshape是一个常数时间复杂度的一个函数，实际上就是没有改变内存中的存储，只是改变了numpy对象x解读时卡维度的位置数据而已，所以不要吝啬于使用它。
对于本任务，由于已经很明确了，所以代码如下：

# GRADED FUNCTION: image2vector
def image2vector(image):
    """
    Argument:
    image -- a numpy array of shape (length, height, depth)
    
    Returns:
    v -- a vector of shape (length*height*depth, 1)
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    v=image.reshape(image.shape[0]*image.shape[1]*image.shape[2],1)
    ### END CODE HERE ###
    
    return v

归一化

我们在机器学习和深度学习中使用的另一种常见技术是对数据进行标准化。 由于归一化后梯度下降的收敛速度更快，通常会表现出更好的效果。 通过归一化，也就是将x更改为$\frac{x}{\Vert x\Vert }$（将x的每个行向量除以其范数）。

这里先对于范数给予说明（复习），范数有很多种，列举两种常用的如下：
1-范数

向量元素绝对值之和

2-范数

向量元素（绝对值的）平方和再开方
而在python中，有专门的归一化工具。直接调用即可
即$np.linalg.norm(x,axis=1,keepdims=True)$函数
其中，说明两点，第一axis=0，即shape[0]，代表操作对象是第一维，也就是上下（同上面shape的部分说明，python使用的是length，height，depth…顺序），而axis=1，即shape[1]代表操作对象是第二维，也就是所谓的左右操作。
而keepdim是为了保证，向量的规模需要被保持，这个知识点很有用，防止我们以后出一些奇奇怪怪的bug。可以参照这位博主举的例子理解keepdims赋值的意义，这里我就暂且不浪费时间再举了https://blog.csdn.net/qq443967620/article/details/104535166

然后就比较简单了。我们得到一个归一化的列向量，然后用原来的矩阵除以这个列向量。代码如下

# GRADED FUNCTION: normalizeRows

def normalizeRows(x):
    """
    Implement a function that normalizes each row of the matrix x (to have unit length).
    
    Argument:
    x -- A numpy matrix of shape (n, m)
    
    Returns:
    x -- The normalized (by row) numpy matrix. You are allowed to modify x.
    """
    
    ### START CODE HERE ### (≈ 2 lines of code)
    x_norm = np.linalg.norm(x, axis = 1, keepdims = True)
    x = x / x_norm
    ### END CODE HERE ###

    return x

广播和softmax函数

这个广播，实际上就是一种策略对齐，简化了很多代码写法使得numpy的向量化操作有时候和单个元素的表达式无比接近。
简单举例说明如下。

import numpy as np

# example of np.exp
x = np.array([1, 2, 3])
y = np.array([4, 5, 6])

print(1/x)
#Output:[1,0.5,0.333333]
print(x+1)
#Output:[2,3,4]Using the broadcast formula

再举例说明，在我们的sigmoid部分，我们使用了对于输入的向量，先计算$a=np.exp(-x)$，再把每一项都加1,$b=a+1$，（运用到广播技术，1被直接扩展成和向量规模一样的全1向量，我们无需再额外生成一个加上去），再每个取倒数，$c=1/b$（也是一种广播技术，其实也是先生成一个全是1的向量，然后逐个做除法）
这样的话，我们最后的写法就和原来对于单个元素的写法没什么区别了，这当然很好。

在这里面softmax代码实现如下：

# GRADED FUNCTION: softmax

def softmax(x):
    """Calculates the softmax for each row of the input x.

    Your code should work for a row vector and also for matrices of shape (n, m).

    Argument:
    x -- A numpy matrix of shape (n,m)

    Returns:
    s -- A numpy matrix equal to the softmax of x, of shape (n,m)
    """
    
    ### START CODE HERE ### (≈ 3 lines of code)
   
    x_exp = np.exp(x)

    x_sum = np.sum(x_exp, axis = 1, keepdims = True)

    s = x_exp / x_sum

    ### END CODE HERE ###
    
    return s

小小结

你需要记住的内容：
-np.exp（x）适用于任何np.array x并将指数函数应用于每个坐标
-sigmoid函数及其梯度
-image2vector通常用于深度学习
-np.reshape被广泛使用。 保持矩阵/向量尺寸不变有助于我们消除许多错误。
-numpy具有高效的内置功能
-broadcasting非常有用

向量化技术

其实向量化技术就是要线性代数好就可以了。没那么多吹的。
几个numpy的乘法函数和线性代数的对应应该是要心知肚明的，先举例说明np.dot

import numpy as np
 
# 2-D array: 2 x 3
two_dim_matrix_one = np.array([[1, 2, 3], [4, 5, 6]])
# 2-D array: 3 x 2
two_dim_matrix_two = np.array([[1, 2], [3, 4], [5, 6]])
 
two_multi_res = np.dot(two_dim_matrix_one, two_dim_matrix_two)
print('two_multi_res: %s' %(two_multi_res))
 #Output:two_multi_res: [[22 28]
 #[49 64]]

# 1-D array
one_dim_vec_one = np.array([1, 2, 3])
one_dim_vec_two = np.array([4, 5, 6])
one_result_res = np.dot(one_dim_vec_one, one_dim_vec_two)
print('one_result_res: %s' %(one_result_res))

#Output:one_result_res: 32

一般来讲，np.dot实现的就是两个矩阵的线性代数乘法运算，如果这是两个行向量，那么比较特殊，会将第二个向量转置，再进行乘法，最后得到运算结果----一个数。

然后呢，再举一些np.multiply的例子

import numpy as np
 
# 2-D array: 2 x 3
two_dim_matrix_one = np.array([[1, 2, 3], [4, 5, 6]])
another_two_dim_matrix_one = np.array([[7, 8, 9], [4, 7, 1]])
 
# 对应元素相乘 element-wise product
element_wise = two_dim_matrix_one * another_two_dim_matrix_one
print('element wise product: %s' %(element_wise))
 #element wise product: [[ 7 16 27]
# [16 35  6]]

# 对应元素相乘 element-wise product
element_wise_2 = np.multiply(two_dim_matrix_one, another_two_dim_matrix_one)
print('element wise product: %s' % (element_wise_2))

#element wise product: [[ 7 16 27]
 #[16 35  6]]

我们便可以发现，multiply实现的是对应位置的乘法。以此类推，numpy支持一系列的逐个对应位置的计算，和各种按照线性代数要求的计算。很容易被搜到，至于另一个np.outer就当额外知识了吧，实际上用.T加上.dot是可以将其完全替代掉的。
最后，这段作业代码如下：

x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]

### VECTORIZED DOT PRODUCT OF VECTORS ###
tic = time.process_time()
dot = np.dot(x1,x2)
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED OUTER PRODUCT ###
tic = time.process_time()
outer = np.outer(x1,x2)
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED ELEMENTWISE MULTIPLICATION ###
tic = time.process_time()
mul = np.multiply(x1,x2)
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED GENERAL DOT PRODUCT ###
tic = time.process_time()
dot = np.dot(W,x1)
toc = time.process_time()
print ("gdot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

实现L1和L2损失函数

-L1损失函数，又称为平均绝对值误差，MAE误差，定义为：

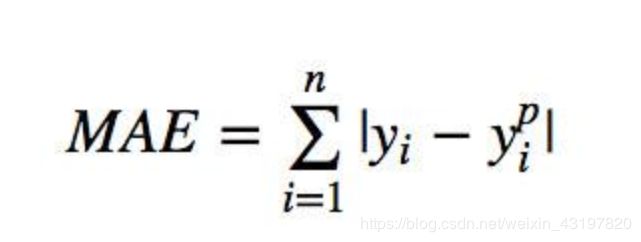
所以其实很简单，我们对于输入的两组向量$y,yhat$，进行做差取绝对值即可。代码如下

# GRADED FUNCTION: L1

def L1(yhat, y):
    """
    Arguments:
    yhat -- vector of size m (predicted labels)
    y -- vector of size m (true labels)
    
    Returns:
    loss -- the value of the L1 loss function defined above
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    loss = np.sum(np.abs(y - yhat))
    ### END CODE HERE ###
    
    return loss

-L2损失函数，又称为均方绝对值误差，MSE误差，定义为：

代码如下

# GRADED FUNCTION: L2

def L2(yhat, y):
    """
    Arguments:
    yhat -- vector of size m (predicted labels)
    y -- vector of size m (true labels)
    
    Returns:
    loss -- the value of the L2 loss function defined above
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    loss = np.dot((y - yhat),(y - yhat))
    ### END CODE HERE ###
    
    return loss

你需要记住的内容：
-向量化在深度学习中非常重要， 它保证了计算的效率和清晰度。
-了解L1和L2损失函数。
-掌握诸多numpy函数，例如np.sum，np.dot，np.multiply，np.maximum等。

第一次作业主要是熟悉一下numpy的各种函数，要做到了解到细节，足够熟练。