深度学习笔记（6）：第一课第二周作业第二部分详解与代码

前言

笔者使用的是下面的平台资源，欢迎大家也一起fork参与到深度学习的代码实践中来。链接如下
https://www.kesci.com/home/project/5dd23dbf00b0b900365ecef1

本章导读

其实还是走的是用神经网络思想去做一个罗杰斯特回归的实践这一思路，而在这一部分，我们的任务是去做一个简单的二分类，构建一个模型，判断图片中的物体是否是猫

题目要求

用神经网络思想实现Logistic回归

欢迎来到你的第一个编程作业！ 你将学习如何建立逻辑回归分类器用来识别猫。 这项作业将引导你逐步了解神经网络的思维方式，同时磨练你对深度学习的直觉。

说明：
除非指令中明确要求使用，否则请勿在代码中使用循环（for / while）。

你将学习以下内容：

• 建立学习算法的一般架构，包括：
  • 初始化参数
  • 计算损失函数及其梯度
  • 使用优化算法（梯度下降）
• 按正确的顺序将以上所有三个功能集成到一个主模型上。

规模查看与重塑训练和测试数据集

很多时候，深度学习中的报错，来自于矩阵向量尺寸的不匹配，这要求我们要对于数据量与数据规模自己要有清醒的认识。
下面我们编码查看训练集和测试集的实例数量：（个人认为在实际应用中这些维度及其对应是和存储的形式息息相关的，也就是说我们要因地制宜的看，不妨我们直接print（x.shape()）将所有信息先都打出来看看。）

### START CODE HERE ### (≈ 3 lines of code)
m_train = train_set_x_orig.shape[0]
m_test = test_set_x_orig.shape[0]
num_px = train_set_x_orig.shape[1]
### END CODE HERE ###

print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))

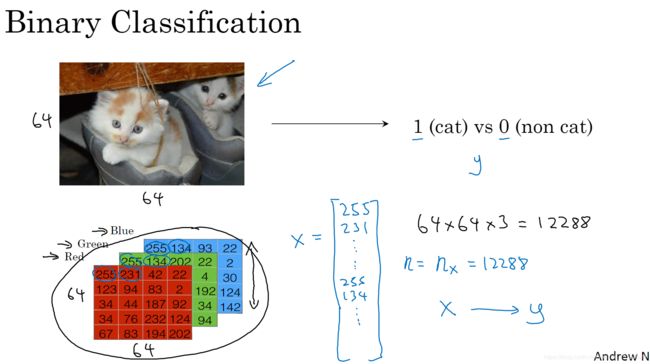
彩色图像，其实就是RG三个通道，本身都是0-255的数据，我们想要将其作为数据训练与预测，方便起见我们先将其平坦化。所以我们来做维度重塑。题目中说的比较清楚了，是将（num_px，num_px，3）展平成(num_px $\ast$ num_px $\ast$ 3, 1)。

这里面有一个小trick。

X_flatten = X.reshape（X.shape [0]，-1）.T     ＃ 其中X.T是X的转置矩阵

解释是这样的，我们拿到这个x的第一维数据大小之后，将其设置为新numpy数组的第一位，然后使用-1这一缺省填充参数，将剩下的所有维度都放置在第二个维度。在本例中，就形成了（209，64×64×3）（其中209是数据个数）这样一个numpy数组，之后再通过转置将其两维度颠倒，这样就得到了平坦化的numpy数组。

之后，为了使得变量有相似的范围，以至于渐变不会爆炸。这是很重要的，所以我们要对其进行标准化处理。一般来讲我们的归一化都是采用行列的范数，但是由于这里面使用RGB通道比较特殊。我们直接将其都除以255即可。

回过头来再看，这其实就是一种将图像数据转化为数字数据的手段，通过上述的平坦化和标准化，预处理完成后，进而便可以进一步用我们的分类模型进行训练与分类。

需要记住的内容：

预处理数据集的常见步骤是：

• 找出数据的尺寸和维度（m_train，m_test，num_px等）
• 重塑数据集，以使每个示例都是大小为（num_px \ * num_px \ * 3，1）的向量
• “标准化”数据

3- 学习算法的一般架构##

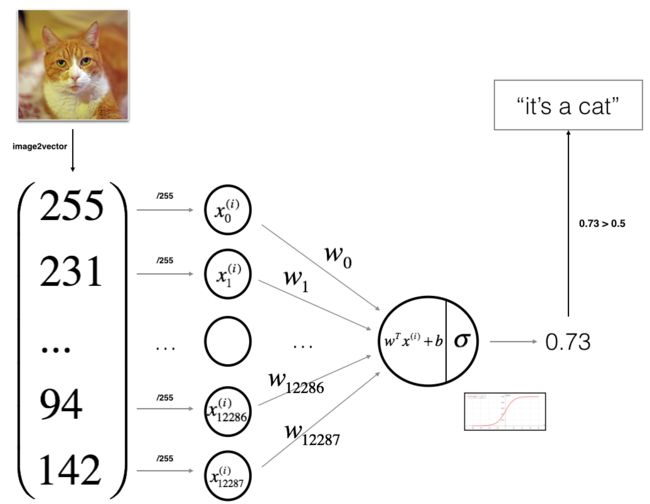
这个图很到位，所以我必须要摘录下来。

算法的数学表达式：

For one example $x^{(i)}$:
$$z^{(i)}=w^T{x}^{(i)}+b\text{\hspace{1em}(1)}$$
$${\hat{y}}^{(i)}=a^{(i)}=sigmoid(z^{(i)})\text{\hspace{1em}(2)}$$
$$\mathcal{L}(a^{(i)},y^{(i)})=-y^{(i)}\log (a^{(i)})-(1-y^{(i)})\log (1-a^{(i)})\text{\hspace{1em}(3)}$$

The cost is then computed by summing over all training examples:
$$J=\frac{1}{m}\sum _{i=1}^m\mathcal{L}(a^{(i)},y^{(i)})\text{\hspace{1em}(6)}$$

关键步骤：
在本练习中，你将执行以下步骤：

• 初始化模型参数
  通过最小化损失来学习模型的参数
  使用学习到的参数进行预测（在测试集上）
  分析结果并得出结论
  

so我们现在开始实践

辅助函数

sigmoid（老生常谈不多废话了）

# GRADED FUNCTION: sigmoid

def sigmoid(z):
    """
    Compute the sigmoid of z

    Arguments:
    z -- A scalar or numpy array of any size.

    Return:
    s -- sigmoid(z)
    """

    ### START CODE HERE ### (≈ 1 line of code)
    s = 1 / (1 + np.exp(-z))
    ### END CODE HERE ###
    
    return s

初始化参数

生成全零的$w$和$b$

# GRADED FUNCTION: initialize_with_zeros

def initialize_with_zeros(dim):
    """
    This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
    
    Argument:
    dim -- size of the w vector we want (or number of parameters in this case)
    
    Returns:
    w -- initialized vector of shape (dim, 1)
    b -- initialized scalar (corresponds to the bias)
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    w = np.zeros((dim, 1))
    b = 0
    ### END CODE HERE ###

    assert(w.shape == (dim, 1))
    assert(isinstance(b, float) or isinstance(b, int))
    
    return w, b

前向和后向传播

现在我们要执行“向前”和“向后”传播步骤来学习参数。即实现函数propagate（）来计算损失函数及其梯度。

提示：

正向传播：

• 得到X
• 计算$A=\sigma (w^{T}X+b)=(a^{(0)},a^{(1)},...,a^{(m-1)},a^{(m)})$
• 计算损失函数：$J=-\frac{1}{m}{\sum }_{i=1}^m{y}^{(i)}\log (a^{(i)})+(1-y^{(i)})\log (1-a^{(i)})$

要使用到以下两个公式：
$$\frac{\partial J}{\partial w}=\frac{1}{m}X(A-Y{)}^T\text{\hspace{1em}(7)}$$
$$\frac{\partial J}{\partial b}=\frac{1}{m}\sum _{i=1}^m(a^{(i)}-y^{(i)})\text{\hspace{1em}(8)}$$
（这里面也是给我一个启发的事情是，当我本打算自己直接现场推导写代码的时候略慌。所以当我们自己设计模型从头编程的时候，或者去做一个衔接时，我们最好也要写下来，否则编码的时候有可能就会很迷茫）

# GRADED FUNCTION: propagate

def propagate(w, b, X, Y):
    """
    Implement the cost function and its gradient for the propagation explained above

    Arguments:
    w -- weights, a numpy array of size (num_px * num_px * 3, 1)
    b -- bias, a scalar
    X -- data of size (num_px * num_px * 3, number of examples)
    Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)

    Return:
    cost -- negative log-likelihood cost for logistic regression
    dw -- gradient of the loss with respect to w, thus same shape as w
    db -- gradient of the loss with respect to b, thus same shape as b
    
    Tips:
    - Write your code step by step for the propagation. np.log(), np.dot()
    """
    
    m = X.shape[1]
    
    # FORWARD PROPAGATION (FROM X TO COST)
    ### START CODE HERE ### (≈ 2 lines of code)
    a = sigmoid(np.dot(w.T,X)+b)
    cost = -1/m*((np.dot(Y,np.log(a).T))+(np.dot(1-Y,np.log(1-a).T)))
    ### END CODE HERE ###
    
    # BACKWARD PROPAGATION (TO FIND GRAD)
    ### START CODE HERE ### (≈ 2 lines of code)
    dw= 1/m*(np.dot(X,(a-Y).T))
    db =1/m*np.sum(a-Y,axis = 1,keepdims = True)
    ### END CODE HERE ###
    assert(dw.shape == w.shape)
    assert(db.dtype == float)
    db = np.squeeze(db)
    cost = np.squeeze(cost)
    assert(cost.shape == ())
    
    grads = {"dw": dw,
             "db": db}
    
    return grads, cost

优化参数（梯度下降）

遵循着 传播、更新参数、再传播…的循环就可以了，梯度下降迭代式子很简单。

# GRADED FUNCTION: optimize

def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
    """
    This function optimizes w and b by running a gradient descent algorithm
    
    Arguments:
    w -- weights, a numpy array of size (num_px * num_px * 3, 1)
    b -- bias, a scalar
    X -- data of shape (num_px * num_px * 3, number of examples)
    Y -- true "label" vector (containing 0 if non-cat, 1 if cat), of shape (1, number of examples)
    num_iterations -- number of iterations of the optimization loop
    learning_rate -- learning rate of the gradient descent update rule
    print_cost -- True to print the loss every 100 steps
    
    Returns:
    params -- dictionary containing the weights w and bias b
    grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
    costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
    
    Tips:
    You basically need to write down two steps and iterate through them:
        1) Calculate the cost and the gradient for the current parameters. Use propagate().
        2) Update the parameters using gradient descent rule for w and b.
    """
    
    costs = []
    
    for i in range(num_iterations):
        
        
        # Cost and gradient calculation (≈ 1-4 lines of code)
        ### START CODE HERE ### 
        grads,cost = propagate(w,b,X,Y)
        ### END CODE HERE ###
        
        # Retrieve derivatives from grads
        dw = grads["dw"]
        db = grads["db"]
        
        # update rule (≈ 2 lines of code)
        ### START CODE HERE ###
        w = w - learning_rate*dw
        b = b - learning_rate*db
        ### END CODE HERE ###
        
        # Record the costs
        if i % 100 == 0:
            costs.append(cost)
        
        # Print the cost every 100 training examples
        if print_cost and i % 100 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
    
    params = {"w": w,
              "b": b}
    
    grads = {"dw": dw,
             "db": db}
    
    return params, grads, costs

得到预测

预测的过程也很简单就是把X带入到我们训练好的参数的模型中，看sigmoid值与0.5的大小，如果大于，那么将其预测为1，否则将其预测为0.

# GRADED FUNCTION: predict

def predict(w, b, X):
    '''
    Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
    
    Arguments:
    w -- weights, a numpy array of size (num_px * num_px * 3, 1)
    b -- bias, a scalar
    X -- data of size (num_px * num_px * 3, number of examples)
    
    Returns:
    Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
    '''
    
    m = X.shape[1]
    Y_prediction = np.zeros((1,m))
    w = w.reshape(X.shape[0], 1)
    
    # Compute vector "A" predicting the probabilities of a cat being present in the picture
    ### START CODE HERE ### (≈ 1 line of code)
    A = sigmoid(np.dot(w.T,X)+b)
    ### END CODE HERE ###

    for i in range(A.shape[1]):
        # Convert probabilities A[0,i] to actual predictions p[0,i]
        ### START CODE HERE ### (≈ 4 lines of code)
        if A[0,i]>0.5:
            Y_prediction[0,i]=1
        else:
            Y_prediction[0,i]=0
        ### END CODE HERE ###
    
    assert(Y_prediction.shape == (1, m))
    
    return Y_prediction

需要记住以下几点：
你已经实现了以下几个函数：

• 初始化（w，b）
• 迭代优化损失以学习参数（w，b）：
  • 计算损失及其梯度
  • 使用梯度下降更新参数
• 使用学到的（w，b）来预测给定示例集的标签

整合模型，完成预测

第一步，初始化参数；
第二步，梯度下降优化；
第三步，预测；
第四步，评估。

# GRADED FUNCTION: model

def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
    """
    Builds the logistic regression model by calling the function you've implemented previously
    
    Arguments:
    X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
    Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
    X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
    Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
    num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
    learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
    print_cost -- Set to true to print the cost every 100 iterations
    
    Returns:
    d -- dictionary containing information about the model.
    """
    
    ### START CODE HERE ###
    
    # initialize parameters with zeros (≈ 1 line of code)
    w,b = initialize_with_zeros(X_train.shape[0])

    # Gradient descent (≈ 1 line of code)
    params, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost = False)
    
    # Retrieve parameters w and b from dictionary "parameters"
    w = params["w"]
    b = params["b"]
    
    # Predict test/train set examples (≈ 2 lines of code)
    Y_prediction_train = predict(w, b, X_train)
    Y_prediction_test = predict(w, b, X_test)

    ### END CODE HERE ###

    # Print train/test Errors
    print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
    print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))

    
    d = {"costs": costs,
         "Y_prediction_test": Y_prediction_test, 
         "Y_prediction_train" : Y_prediction_train, 
         "w" : w, 
         "b" : b,
         "learning_rate" : learning_rate,
         "num_iterations": num_iterations}
    
    return d

学习率的选择

为了使梯度下降起作用，必须明智地选择学习率。 学习率$\alpha$决定我们更新参数的速度。 如果学习率太大，我们可能会“超出”最佳值。 同样，如果太小，将需要更多的迭代才能收敛到最佳值。 这也是为什么调整好学习率至关重要。记住这一部分是经验相关，但是也是可以进行调整的。

此作业要记住的内容：

1. 预处理数据集很重要。
2. 如何实现每个函数：$initialize（），propagation（），optimize（），$并用此构建一个$model（）$。
3. 调整学习速率（这是“超参数”的一个示例）可以对算法产生很大的影响。 你将在本课程的稍后部分看到更多示例！