主成分分析-python机器学习实现(PCA)

代码思路来自Python Machine Learning 3rd，本人只是做了一些修改

numpy + pandas实现

我们以pandas内置的wine库来实现，我这里采取的是本地读取

import pandas as pd
df_wine = pd.read_csv('./wine.data')

1. 标准化原始数据集

# 首先分离数据集
from sklearn.model_selection import train_test_split
X, y = df_wine.iloc[:, 1:], df_wine.iloc[:, 0]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, stratify=y, random_state=0)

# 标准化
from sklearn.preprocesssing import StandardScalor
sc = StandardScalor()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)

2. 获得协方差矩阵

使用numpy API

import numpy as np
cov_mat = np.cov(X_train_std.T)

3. 获得特征向量和特征值

使用numpy API

eigen_vals, eigen_vecs = np.linalg.eigh(cov_mat)

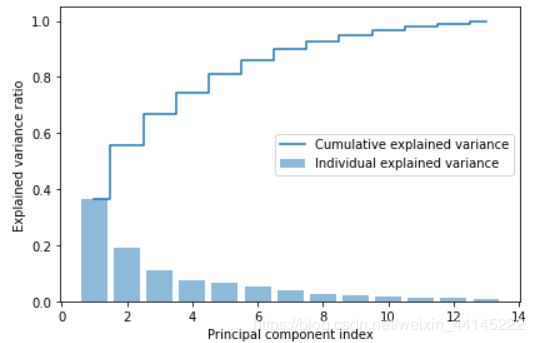
4. 按照特征值降序排列相应的特征向量

tot = sum(eigen_vals)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp）

可视化：

import matplotlib.pyplot as plt
# 画直方图
plt.bar(range(1, 14), var_exp, alpha=0.5, align='center', label='Individual explained variance')
# 画阶梯图
plt.step(range(1,14), var_exp_sum. where='mid', label='Cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

结果：

5. 选择k个特征值最大的特征向量

# 获得特征对，由特征值和其对应的特征向量组成一组特征对
eigen_pairs =  [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]

eigen_pairs.sort(key=lambda k: k[0], reverse=True)

说实话这里使用lambda方程实现排序我没弄懂，先记在这里，期待大佬解答

6. 获得k维矩阵，W

# 这里之选两个维度
w = np.stack((eigen_pairs[0][1])[:, np.newaixs],(eigen_pairs[1][1][:, newaixs]))
print(f'Matrix W: {w}')

7. 使用W实现维度转换

X_train_pca = X_train_std.dot(w)

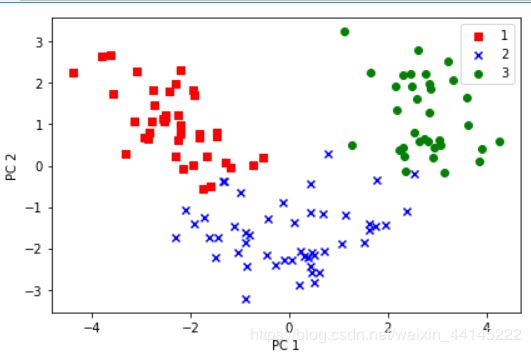
可视化:

colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
	plt.scatter(X_train_pca[y_train==l, 0], X_train_pca[y_train[y_train==l, 0], c=c, label=l, marker=m)
	plt.xlabel('PC 1')
	plt.ylabel('PC 2')
	plt.legend(loc='best')
	plt.tight_layout()
	plt.show()

结果：

sickit-learn直接实现

直接实现的话直到套路就够了，代码中的数据沿用了之前标准化后数据，因此没有包括数据标准化的过程，请注意

from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
# 1.标准化，同上
...
# 2.初始化PCA和逻辑回归模型
pca = PCA(n_components=2)
lr = LogisticRegression(multi_class='ovr', random_state=1, solver='lbfgs')
# 3.训练PCA模型实现数据降维
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
# 4.训练逻辑回归模型进行预测
lr.fit(X_train_pca, y_train)
lr.predict(X_test_pca)
# 5.绘图
plot_decision_regions(X_train_pca, y_train, classifier=lr):
	pass

从这里我们可以更加清晰地发现，使用pca进行数据降维时，不需要用到y_train，即数据没有明确的标签（虽然说酒数据里有标签，但是也可以用） 因此pca一般用于非监督学习，感兴趣可以查看适用于监督学习的数据降维方法简明LDA

结果：