数学建模算法:层次分析法之如何选择旅游目的地
世界那么大,我们都想去看看,
但是我们该怎么选择自己的旅游目的地呢?到底是先考虑囊中羞涩还是山高路远,又或者是把风光旖旎作为首选?
是不能忍受茅屋采椽,是舍弃不下唇口舌尖的,一丝嚼劲,一丝脆甜,还是挑战,登峰造顶,勇攀高峰
本文通过层次分析法来,综合考虑以上所有因素选择出一个也许并不完美,但最合适你的旅游目的地
本文分为四个部分来例说此法:
一:层次分析法的应用.
二:层析分析法的实现步骤.
三:层析分析法代码实现.
四:代码输出结果分析.
一:层次分析法的应用
1.1层次分析法是上个世纪美国国防部在研究 “ 根据各个工业部门对国家福利的贡献大小来电力分配 ” 时提出的方法。
用于决策面临多种方案,是要根据一定的标准来选择某一种方案。
1.2具体实例
比如说在不同牌子的电冰箱中,我们选购一种是要考虑品牌的信誉,冰箱的功能,价格,耗电量和我们的主要用途。
那么怎么把这些偏定性的问题用定量的问题来解决呢?
层次分析法根据因素之间的相互关联,按照不同的层次把它组合,形成一个多层次的分析结构。
二:层析分析法的实现步骤
层次分析法构建模型的4个步骤大致分为:
1.建立层次结构模型
2.构造判断矩阵或对比矩阵
3.层次单排序及其一致性检验
4.层次的总排序及其一致性检验
我们依次解决这四步:
2.1.如何构建层次结构模型呢?
我们把将 决策的目标,考虑的因素,还有决策对象按照它们之间的相互关系分为最高层,中间层和最低层。
最高层:是我们决策的目的和解决的问题
最低层:决策的备选方案,
中间层:考虑的因素和决策的准则。
详解如图:
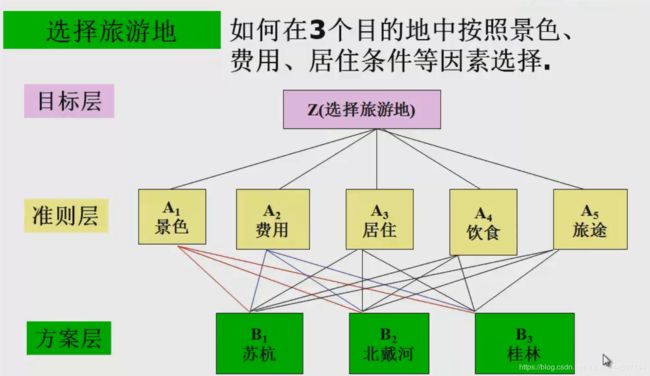
在如何选择旅游地这一事例中,准则层里面还可以加,比如说:安全系数,交通是否便利等等因素。
接下来我们就要确定各层次各因素的权重,比如说我们认为,这次旅行的安全是最重要的,那么我们可以给他这个权重赋值10,接下来景色也很重要,将它赋值8,最不重要的比如说是距离,将它赋值为1。
但这样感觉,特别的随意,而且常常这个模型不能够推广,也不容易被别人接受,主观性太强。
所以Santy先生提出了一致矩阵法。
2.2.构造判断矩阵或对比矩阵
一致矩阵法的核心如下:
第一点,不把所有的因素放在一起比较,只是两两之间相互比较,
第二点,是对比的时候采用相对的尺度,尽量减少因为性质不同而造成的各个因素之间相互比较的困难,以提高准确度。
我们可以参考成对比较矩阵的标度表。

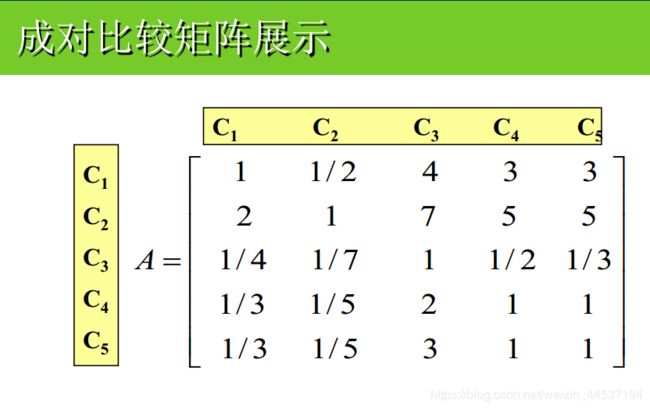
简单解释如下:在这个矩阵里面C1比C1是1,他自己和自己比肯定都是一样重要的。
c1:c2是1:2。那么c2比c1稍微重要一些,而且这个重要程度要少于标度表中的 “ 稍微重要”。
C1比C4,那么也就是说C1比C4要重要。
在具体分析情况的时候,我们先把C1,C2这些因素给列出来,然后再在矩阵里面填相对应的系数。
我们最后将代码写完之后,只需要修改成对比较矩阵的里面的不同的数字,它自己就可以将权重算出来。
2.3.层次单排序及其一致性检验,
我们接下来看一致性检验的问题。
例如,在此表中,根据c2,c1和c2,c3的关系,我们推出来了c2和c3的关系。
但是矩阵和我们推出来的不一致。

这就涉及到一致性检验,我们可以允许不一致的情况,但是一定要确定不一致的允许范围。
(一致性检验不算是重点,不需要手工计算,我们程序中已经做了限定,如果说验证通过的话他才可以输出)
我们在构造成对比较的时候把两侧的a1,a2都写清楚,方便填入,我们通过查阅了相关资料之后,来填好这个矩阵
A矩阵就是,A1,A2,A3,A4,A5(景色费用,居住,饮食,旅途)这5个因素之间的重要程度构成的一个矩阵。
而B1矩阵是B1,B2,B3三个因素相对于A1(景色)这个评定方式下的三个因素之间的重要程度构成的矩阵。

不同的矩阵之间确定的这些系数,我们通过查阅资料和自己主观判断来填写完成。
三:层析分析法代码实现
程序代码如下
disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>p
i=i+1;
x(:,i)=A*y(:,i-1);
m(i)=max(x(:,i));
y(:,i)=x(:,i)/m(i);
k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);
%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
end
测试矩阵:
[1, 1/2, 4, 3, 3;
2, 1, 7, 5, 5;
1/4, 1/7, 1, 1/2, 1/3;
1/3, 1/5, 2, 1, 1;
1/3, 1/5, 3, 1, 1;]
[1,2,5;
1/2,1,2;
1/5,1/2,1;]
[1,1/3,1/8;
3,1,1/3;
8,3,1;]
[1,1,3;
1,1,3;
1/3,1/3,1;]
[1,3,4;
1/3,1,1;
1/4,1,1;]
[1,1,1/4;
1,1,1/4;
4,4,1;]
四:代码输出结果分析
数模中我们不需要考虑这些代码是怎么编写的,只要将分析矩阵的系数写清楚就行,运行代码后,结果显示此矩阵的一致性可以接受就达成目标。

这里的 CI 代表第1个A矩阵这5个因素相对于旅游地的重要程度产生的权重
我们可以看出第2个因素,它的权重是0.4758是最高的,查看后第2个因素是费用,则我们得出:费用在旅游地的选择中占比权重最高。
我们将B3矩阵,放入程序中运行,结果显示三个权重分别为0.42860.4286和0.1429,也就是说B1,B2(苏杭和北戴河)的居住环境好于B3桂林。

计算层次的总权值:
例如:B1对总目标的权值为:A1对总目标的权值0.595乘以B1对A1的权值0.263,再加上A2对总目标的权值0.082于B2对A2的权值0.475的乘积…


最后的决策层对于总目标的全向量(如图所示),也就是说,根据我们所给的数据系数,我们选择旅游地,评定得出 桂林是您的最佳的旅游地。