Bias偏差 and Variance方差 概念简单理解
Bias偏差 and Variance方差
以下内容依照原文有修改一些, 加上一些自己的理解让初学更好去记忆
中间有夹杂原文与中文,是想说这些专有的名词最好也要熟悉, 毕竟论文都还是以英文为主的, 有时候英语确实能更直观的感受到意思
正文
我们要如何得知一个模型的跑出来的效果好不好?就取决于模型的预测能力以及在测试集上的泛化能力
假如今天我们要预测一下中国人喜欢复联4的人多还是喜欢玩具总动员4的人多, 我们去了上海大街上随机访问了100位, 其中44人表示喜欢玩具总动员4, 40位表示更喜欢复联4, 而有16位表示没意见, 基于这个访问, 我们就能断定全中国喜欢玩具总动员的人更多吗?
显然是不行 ! 如果我们今天去到北京或者广州其他地方, 答案都有可能不同,我们能观察到这次预测的"“不一致性”, 就说明了前次的访问没办法代表我们的最佳预测
这也很像多个平行宇宙, 在另一个时空的宇宙中, 每个人虽然都存在但想法可能不同, 甚至命运也不同
那么重点来了
一个模型能够在最终测试上可以将错误率降到最低, 那说明这个模型是work的, 我们就要面对这个error好好的考究一番, 究竟error是什么? 只是单纯的差值就会影响模型效率吗?
下面我们对error要有更深的理解才可以
了解敌人才能战胜
Error = sum of all(实际-预测)
我们把每一次预测错误值总和起来, 公式如
L ( x , y ) = ∑ k = 1 N ( y − f ( x ) ) L(x, y )=\sum_{k=1}^{N}(y-f(x)) L(x,y)=k=1∑N(y−f(x))
Error = Reducible Error + Irreducible Error
用公式表达
E r r ( x ) = ( f ( x ) − 1 k ∑ i = 1 k f ( x i ) ) 2 + σ ε 2 k + σ ε 2 Err(x) = \left(f(x) -\frac{1}{k}\sum_{i=1}^{k}f(x_i)\right)^2 + \frac{\sigma_{\varepsilon}^{2}}{k} + \sigma_{\varepsilon}^{2} Err(x)=(f(x)−k1i=1∑kf(xi))2+kσε2+σε2
Err(x) = Bias^2 + Variance + Irreducible error
也就是说Error主要是由两大块差值所组成的
这里的Irreducible error是无法降低的无论你应用什么样的演算法, 通常是由unknown的变量所造成, 我觉得这种error可以理解为无论一个艺人明星, 做的在棒拍了在多部大片, 还是会有人不认同不喜欢, 你没有办法让全世界的人都喜欢你
所以剩下 Reducible Error 是我们要面对的
Reducible error 是由由bias + Variance所组成
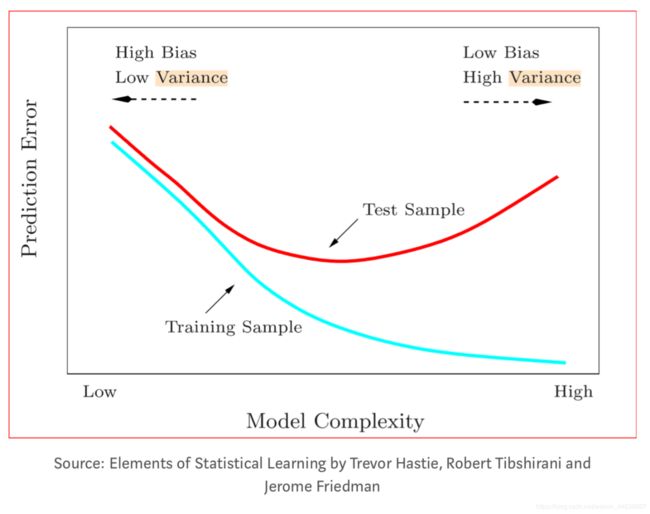
这两个因素就是造成我们模型 underfitting 以及 overfitting 的主要原因
如果我们能把bias 以及 Variance都降到很低, 那对模型来说肯定是好的
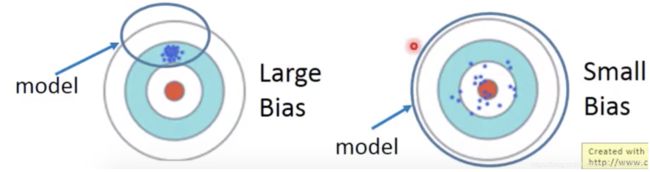
Bias(偏差)
Bias 就是你平均预测值以及实际值的差异, 如果平均预测值与实际值相差甚远, 就表示Bias非常高, Bias过高的时候导致演算法会忽略掉输入与输出变量之间的关联性, 当你的model有很高的bias,就说明你的模型太过简单,无法准确的获取input的信息造成 underfitting 问题, 所以无论在训练集或者在测试集都没有很好的表现(high error, low acc)
PS. 我们能理解bias为平均误差, 而不只是单一次预测的error
Variance(方差)
Variance也是一种误差,而Variance的值大小取决于你的样本数大小, 也就是公式中的k值
σ ε 2 k \frac{\sigma_{\varepsilon}^{2}}{k} kσε2
是发生在每一次不同data训练时产生的, 而Variance过大的时候也就是我们熟知的过拟合(overfitting)问题
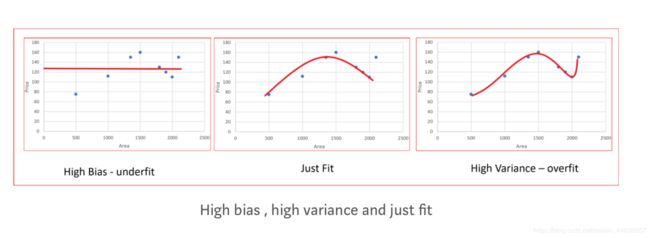
从图表中可以清楚的看到
-
high bias :线段简单, 根本无法拟合这些预测数据点
-
Just fit :可以拟合大部分的预测数据点
-
High Varience:几乎拟合了所有的预测数据点,让model本身变的最复杂,过拟合就是这个意思,在这个数据集上表现的很好, 但只要一碰上 新面孔就表现的却场
就好比平时熟悉的异性对象打打闹闹的,但 一看见没见过的顶级美女走来就紧张的语无伦次
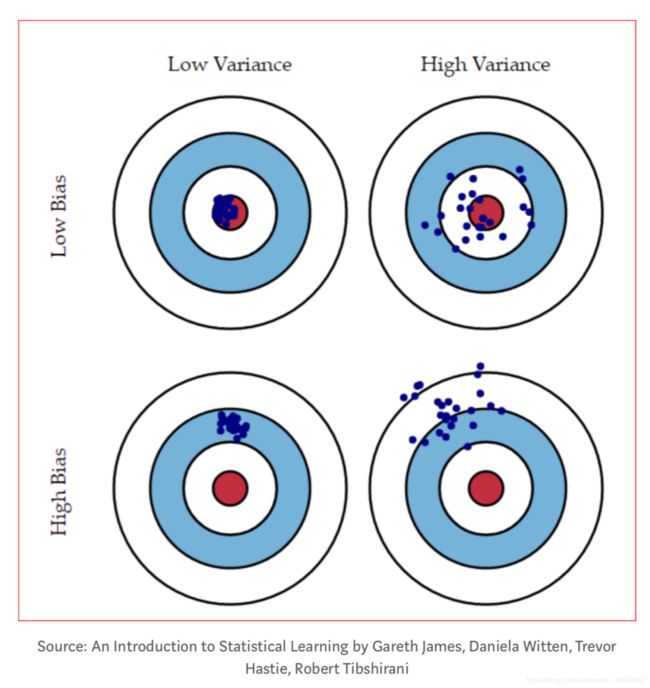
可以清楚看到左上角 Low Varience and Low Bias是我们最希望模型达到的效果,数据点正中红心
其余三个点
-
High Bias Low Variance: Models有着还不错的相容性(点聚合), 但是预测精度不佳
-
High Bias High Variance : Model 预测精度不好又没有很好的一致性(inconsistent)(点分散)
-
Low Bias High variance:Models 有着不太令人满意的预测精度也没有很好的一致性(点分散)
我们可以得出一些结论
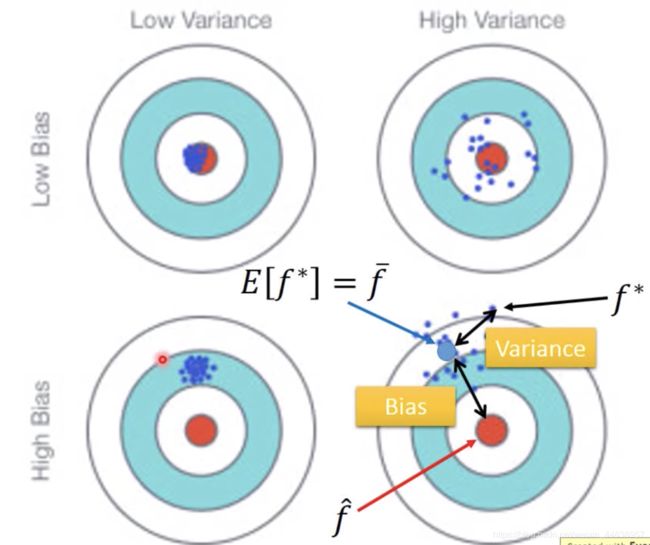
- 对于Variance来说, 简单的model, 较不容易受到data的影响:举个极端例子, 将model定义为 f(x) = c, 则不管输入什么样的data, output就是c, 尽管找再多的dataset训练的结果还是一样c, 此时Variance就是0 , 所以相反的 model的复杂程度提高了的话, 输出的就不只是c, 也会随着input data的不同, 输出也会各式各样, 也就是上图看见的点非常的分散
- 对于Bias来说, 简单的model,bias偏大, 复杂的model, bias偏小:我们可以这样理解, 简单的model所产生的function space范围比较小,在没有包含target(红心)的情况下, 怎么train也不会让bias变小,而 复杂的model产生的范围更大, function space也许有包含target, 但training data不够多, 所以每次找出来的点都不同, 就会分散 如下图:
- 总结上述两个点,
- 当model简单的时候, Variance比较小, Bias偏大,就是underfitting
- 当model复杂的时候, Variance比较大, Bias偏小, 就是overfitting
- 必须找到一个平衡点兼顾Variance以及Bias
所以我们如何从结果去判断我们当前的训练是否有过高的bias 或者是 Variance呢?
High bias:
-
High training error
-
Validation error or test error is same as training error
就是无论在训练及测试上都表现的奇差
High Variance:
-
low training error
-
high validation and test error
白话一些就是你在训练集上跑的很好, 但是面对从未跑过的测试集时,错误率竟然高的多
经过分析确认你的模型问题出在哪之后, 该怎么做呢? 以下几个思路可以走走
High bias solution:
- 增加更多输入的特征(就是改你的网络, 说明你的model根本没办法抓到特征啊!!)
- 利用建构多项式特征来增加feature的复杂度(sklearn包可以了解)
- 减少正则化(Regularization)
High Variance solution:说白点就是为了解决过拟合(overfitting)问题
- 增加训练集样本数, 但我知道听起来简单, 实际上很难,那么数据增强也是可以的啊
- 减少输入的特征 (Dropout, relu…)
- 增加正则化(Regularization)
总结:
这是一个鱼与熊掌不得兼得的故事, 模型没有办法在同一个时间段拥有两种复杂程度的(例如同时有两种参数量的model可以应付不同状况,这是目前做不到的),我们能做的就是在bias 以及 Variance之间找到一个绝佳的平衡点, 让模型训练过程不会出现underfitting跟overfitting的问题
参考资料:
http://scott.fortmann-roe.com/docs/BiasVariance.html
https://towardsdatascience.com/understanding-the-bias-variance-tradeoff-165e6942b229
https://medium.com/datadriveninvestor/bias-and-variance-in-machine-learning-51fdd38d1f86
https://stats.stackexchange.com/questions/135960/difference-between-bias-and-error
台大李宏毅油管视频