trilateration三边测距算法及C语言实现(适用stm32)
我们经常会使用UWB进行室内的简单定位工作,其使用的算法多种多样,今天简单介绍一下trilateration三边测距算法,这个算法很好理解,同时代码实现起来也不是很困难。
算法解析
1、已知三点位置 (x1, y1), (x2, y2), (x3, y3)
2、已知未知点 (x0, y0) 到三点距离 d1, d2, d3
以 d1, d2, d3 为半径作三个圆,根据毕达哥拉斯定理,得出交点即未知点的位置计算公式:
( x1 - x0 )2 + ( y1 - y0 )2 = d12
( x2 - x0 )2 + ( y2 - y0 )2 = d22
( x3 - x0 )2 + ( y3 - y0 )2 = d32
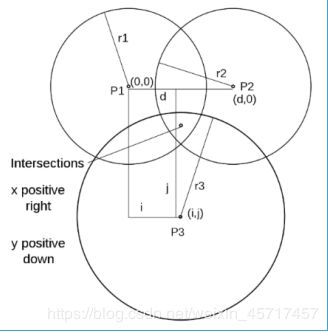
设未知点位置为 (x, y), 令其中的第一个球形 P1 的球心坐标为 (0, 0),P2 处于相同纵坐标,球心坐标为 (d, 0),P3 球心坐标为 (i, j),三个球形半径分别为 r1, r2, r3,z为三球形相交点与水平面高度。则有:
r12 = x2 + y2 + z2
r22 = (x - d)2 + y2 + z2
r32 = (x - i)2 + (y - j)2 + z2
当 z = 0 时, 即为三个圆在水平面上相交为一点,首先解出 x:
x = (r12 - r22 + d2) / 2d
将公式二变形,将公式一的 z2 代入公式二,再代入公式三得到 y 的计算公式:
y = (r12 - r32 - x2 + (x - i)2 + j2) / 2j
代码实现
该代码是需要输入四个基站坐标和四个基站到未知点的距离的, 因为一般实际工程中最少都是使用四个基站,如果需要改成三个直接引用 trilateration(AX, AY, d1, BX, BY, d2, CX, CY, d3); 即可。4个基站只是在三个基站的基础上来解析的,多了一步对4种不同的三个基站的定位位置数据平均化。
同时,此代码与上文的解算过程略有出入,在后面会进行解释。
.h文件代码:
#ifndef __MY_LOCATION_H
#define __MY_LOCATION_H
static int AX,BX,CX,DX,AY,BY,CY,DY;
void MY_location_Init(int X1, int Y1, int X2, int Y2, int X3, int Y3,int X4,int Y4);
double* trilateration(double x1, double y1, double d1, double x2, double y2, double d2, double x3, double y3, double d3);
double* Printf(double d1, double d2, double d3, double d4);
int P(int x, int n);
#endif
.c文件代码
#include"MY_Location.h"
/*
??:?x?y??
*/
int P(int x, int n)
{
int val = 1;
while (n--)
val *= x;
return val;
}
void MY_location_Init(int X1, int Y1, int X2, int Y2, int X3, int Y3,int X4,int Y4)
{AX=X1; AY=Y1; BX=X2;BY=Y2; CX=X3; CY=Y3 ;DX=X4,DY=Y4;}
/*
??:??????????
???????
*/
double* trilateration(double x1, double y1, double d1, double x2, double y2, double d2, double x3, double y3, double d3)
{
static double d[4] = { 0.0,0.0 };
double a11 = 2 * (x1 - x3);
double a12 = 2 * (y1 - y3);
double b1 = P(x1, 2) - P(x3, 2) + P(y1, 2) - P(y3, 2) + P(d3, 2) - P(d1, 2);
double a21 = 2 * (x2 - x3);
double a22 = 2 * (y2 - y3);
double b2 = P(x2, 2) - P(x3, 2) + P(y2, 2) - P(y3, 2) + P(d3, 2) - P(d2, 2);
d[0] = (b1 * a22 - a12 * b2) / (a11 * a22 - a12 * a21);
d[1] = (a11 * b2 - b1 * a21) / (a11 * a22 - a12 * a21);
return d;
}
double *Printf(double d1, double d2, double d3, double d4)
{
double *Coordinate_A = 0, *Coordinate_B = 0, *Coordinate_C = 0, *Coordinate_D = 0;
static double XY[2] = { 0,0 };
Coordinate_A = trilateration(AX, AY, d1, BX, BY, d2, CX, CY, d3);
Coordinate_B = trilateration(AX, AY, d1, BX, BY, d2, DX, DY, d4);
Coordinate_C = trilateration(AX, AY, d1, CX, CY, d3, DX, DY, d4);
Coordinate_D = trilateration(BX, BY, d2, CX, CY, d3,DX, DY, d4);
XY[0] = (Coordinate_A[0] + Coordinate_B[0] + Coordinate_C[0] + Coordinate_D[0]) / 4;
XY[1] = (Coordinate_A[1] + Coordinate_B[1] + Coordinate_C[1] + Coordinate_D[1]) / 4;
return XY;
}
代码调用:先初始化基站坐标
MY_location_Init(0, 0,600, 0, 0,600,600,600);//初始化基站坐标
coordinate= Printf(D1,D2,D3,D4);//输入基站分别到未知点的坐标
printf("X%dY%d",(int)coordinate[0],(int)coordinate[1]);//输出格式
调用的时候 需要先在MY_location_Init(int X1, int Y1, int X2, int Y2, int X3, int Y3,int X4,int Y4);中输入基站的位置坐标。
注意:此代码可直接复制到stm32的代码中使用。
敏感性分析
在实际的测量中,往往由于测量的误差,使三个圆并不交于一点,而相交于一块区域。在此种情况下,便需用其他算法进行求解,如极大似然估计法,最小二乘法进行估计,或者使用三角形质心算法。上面的代码就是使用的最小二乘算法。
同时,由无线信号强度渐变模型我们可以发现,当定位终端离基站距离越远时,接收到的RSSI值变化会越来越小,这就会导致距离越远,基站与定位终端的距离误差越大,相应的造成定位误差变大,由此,我们可以采取加权的思想,将距离小的(精确度高)赋予较大的权值,距离大的(精确度低)的赋予较小的权值。