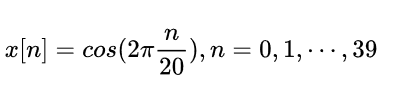matlab常用函数之傅里叶变换&傅里叶级数&频谱分析（1）

一、连续时间

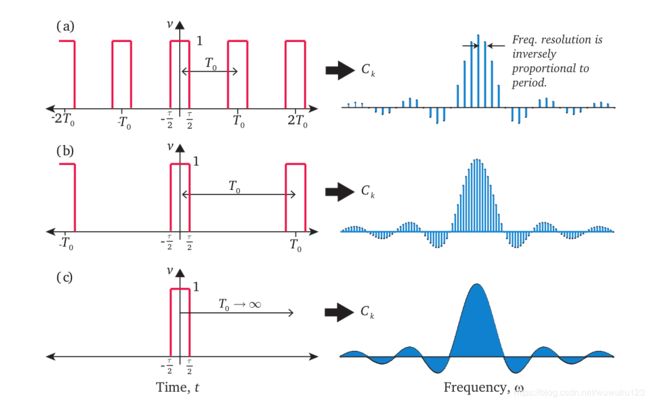
从傅里叶级数(FS)到傅里叶变换(FT)（周期信号到非周期信号）

（1）任意周期函数都可以写成三角函数之和。

（2）傅立叶级数是针对周期函数的，为了可以处理非周期函数，需要傅立叶变换。

既：

二、离散时间

从傅里叶级数到傅里叶变换（周期信号到非周期信号）

理解一个公式：

• y=A*cos(ω*t+φ)+b（A＞0，0＜φ＜π/2）；
• y=A*cos(（2*pi/T）*t+φ)+b（A＞0，0＜φ＜π/2）；% T为余弦信号(y)的周期；
• y=A*cos((2*pi*f)*t+φ)+b（A＞0，0＜φ＜π/2）；% f为信号频率

抛开时间抛开采样频率，只看点的个数，我们对某个余弦信号在两个周期内采样了40次：如下：

matlab画图：

n = 0:39;
y = cos(2*pi*(2*n)/40);
stem(n,y);
figure
plot(n,y)

频率信号：

stem(n, abs(fft(y)));

• 信号频率：以余弦函数表达式为例：y=A*cos((2*pi*f)*t+φ)+b（A＞0，0＜φ＜π/2）；% f为信号频率

信号频率为 f；如果要对其信号进行采样，必须满足奈奎斯特采样定率，即采样频率(Fs)大于2*f HZ；

• 采样频率Fs/采样周期Ts：
• 频率分辨率/频率间隔：Fs/N  100/40=2.5

以上面介绍为例：

上面的信号是40个采样，如果给一个采样频率是100Hz，那么信号长度就是0.4s，原信号在40个采样内振动了两个周期，可以算出其频率为5Hz。

对于频域，每个“在40个采样内振动了k个周期”的基信号的实际频率为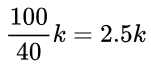 ，也就是说频域图中的每一个点代表2.5Hz，这个系统的频域分辨率是2.5Hz，所以原信号的实际频率为

 

三、采样频率和信号带宽

1、采样频率：

采样频率，也称为采样速度或者采样率，定义了每秒从连续信号中提取并组成离散信号的采样个数，它用赫兹（Hz）来表示。采样频率的倒数是采样周期或者叫作采样时间，它是采样之间的时间间隔。通俗的讲采样频率是指计算机每秒钟采集多少个信号样本。

采样定理是指，如果信号带宽不到采样频率的一半（即奈奎斯特频率），那么此时这些离散的采样点能够完全表示原信号。高于或处于奈奎斯特频率的频率分量会导致混叠现象。大多数应用都要求避免混叠，混叠问题的严重程度与这些混叠频率分量的相对强度有关。

2、信号带宽：

由信号频谱图可以观察到一个信号所包含的频率成分。把一个信号所包含谐波的最高频率与最低频率之差，即该信号所拥有的频率范围，定义为该信号的带宽。因此可以说，信号的频率变化范围越大，信号的带宽就越宽。

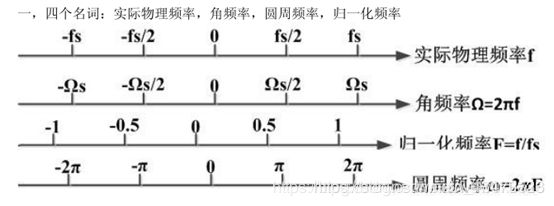
四、角频率、归一化频率

1、实际信号的物理频率f：

表示AD采集物理信号的频率，fs为采样频率，由奈奎斯特采样定理可以知道，fs必须≥信号最高频率(f)的2倍才不会发生信号混叠，因此fs能采样到的信号最高频率为fs/2。单位：Hz

2、角频率(角速度)Ω/模拟频率：

是实际物理频率f的2*pi倍，这个也称模拟频率，单位: rad/s。

Ω=2pi*f=2pi/T，T=1/f=2pi/Ω

3、归一化频率：

是将物理频率f按fs归一化之后的结果，最高的信号频率为fs/2对应归一化频率0.5。这也就是为什么在matlab的fdtool工具中归一化频率为什么最大只到0.5的原因。 单位：无。

4、圆周频率w/数字频率 ：

是归一化频率的2*pi倍，这个也称数字频率。数字频率w：单位: rad。

w=2*pi*(f/fs)=ΩTs=Ω/fs

举例：

假定有一个正弦信号x[n]，其频率f=100Hz，幅度为A，初始相位为0，则这个信号用公式可以表示为：

x(t) =A*sin(2*pi*100*t)

用采样频率fs=500Hz对其进行采样，得到的数字信号x[n]为：

x[n] =A*sin(2*pi*100*n/fs)= A*sin(0.4*pi*n)

很明显，这个数字信号的频率为0.4pi 。

 

 

 

参考：

1、如何理解傅立叶级数公式？

2、如何通俗地解释欧拉公式（e^πi+1=0）？

3、 如何通俗地理解傅立叶变换？

4、 从傅立叶级数到傅立叶变换

5、采样频率

6、信号带宽

7、数字角频率和模拟角频率和物理频率和归一化角频率的关系，及FFT频率和实际物理频率的关系分析

8、模拟角频率和数字角频率的关系

9、如何通俗地解释泰勒公式？