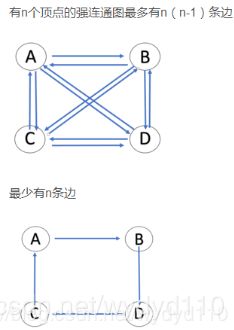
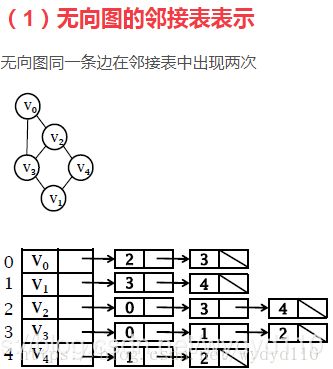
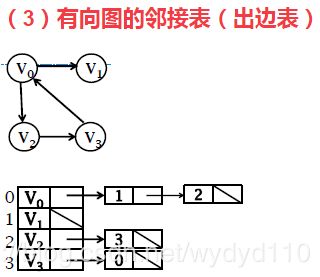
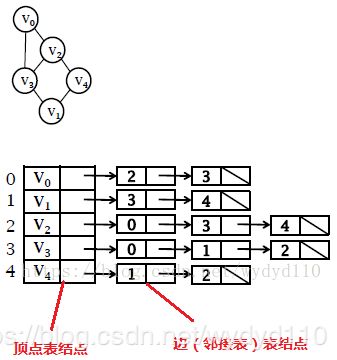
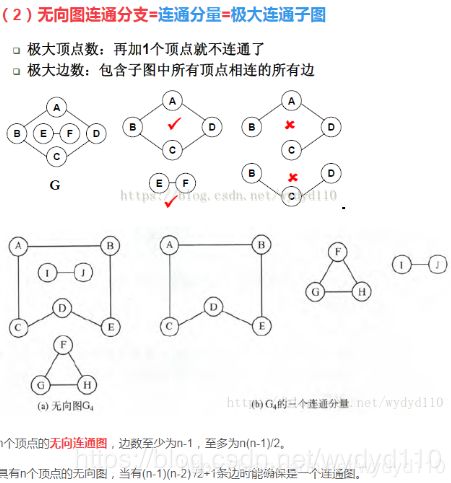
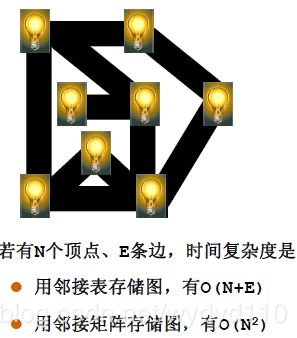
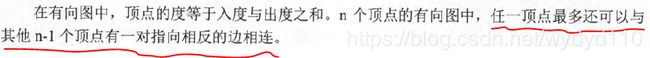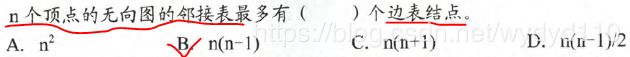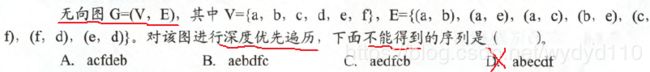数据结构图题库
王道压缩矩阵的题在栈与队列里
网络课课后题
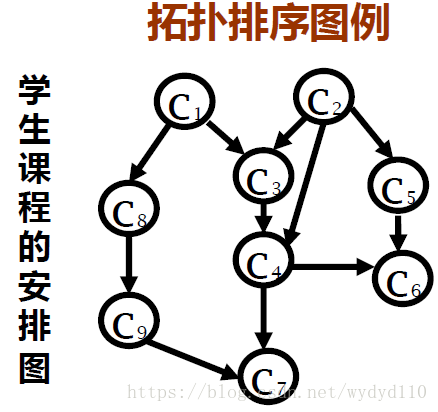
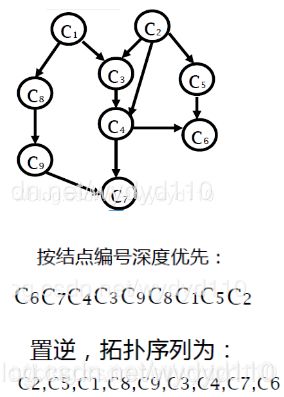
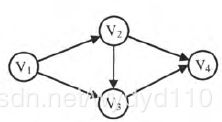
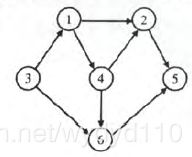
1、有向图G如下图所示，请写出所有拓扑排序序列。所有的顶点都直接用其数字标号表示，如拓扑排序序列为
，那么请写成1234（中间没有空格）。不同的拓扑排序序列按照字典序排序，中间用一个空格隔开。
解析：
根据拓扑排序的定义，顶点1必须在顶点3前，顶点1、顶点2和顶点3必须在顶点4前，故排列可以为1234、1324、2134
答案： 1234 1324 2134
扩充例子：
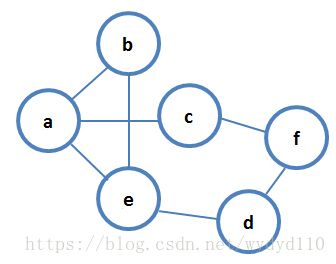
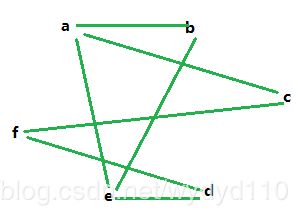
2、无向图G=(V, E)，其中：V={a, b, c, d, e, f}, E={(a, b), (a, e), (a, c), (b, e), (c, f), (f, d), (e, d)}，对该图进行深度优先遍历（优先访问编号小的结点），得到的顶点序列为？
| A、abedfc |
| B、aebdfc |
解析：
根据深度优先的算法，先访问a，再访问a的邻接顶点b，再访问b的邻接顶点e，访问e的邻接顶点d，访问d的邻接顶点f（注意是无向图），访问f的邻接顶点c，不再有没访问的顶点，结束。
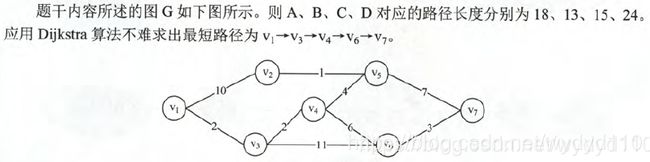
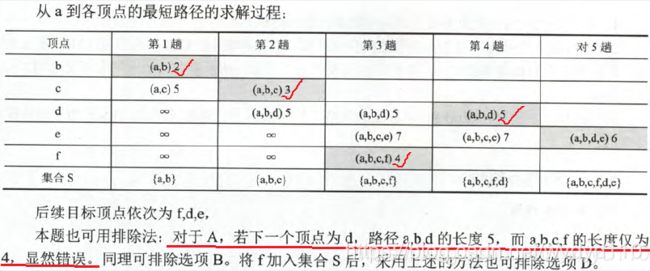
3、下列关于最短路算法的说法正确的有：
A、当图中不存在负权回路但是存在负权边时，Dijkstra算法不一定能求出源点到所有点的最短路。
解析：即使是只有负权边，也会导致以前已经被选出来更新其它结点最短路值的结点的最短路值被更新，造成错误。
B、当图中不存在负权边时，Dijkstra算法能求出每对顶点间最短路径。
解析：可以执行多次Dijkstra算法实现这一要求。
C、当图中存在负权回路时，Dijkstra算法也一定能求出源点到所有点的最短路。
解析：Dijkstra算法无法处理图中存在任何负权边的情况。
D、Dijkstra算法不能用于每对顶点间最短路计算。
解析：可以执行多次Dijkstra算法实现这一要求。
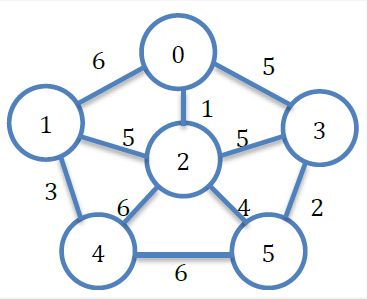
4、请使用Kruskal算法求出下图的最小生成树，依次写出每次被选择的合法的合并代价最小的边的编号（如果同时存在多条边满足要求，选择编号最小的）。顶点a到顶点b (a < b)之间的边编号为ab，例如图中权值为1的边编号为02。
解析
Kruskal算法优先选择权值小的边，先挑选权值为1的边02，再选择权值为2的边35，再选择权值为3的边14，再选择权值为4的边25，再选择权值为5的边，只有选择12才能连接两个不同的连通分支
答案： 02 35 14 25 12
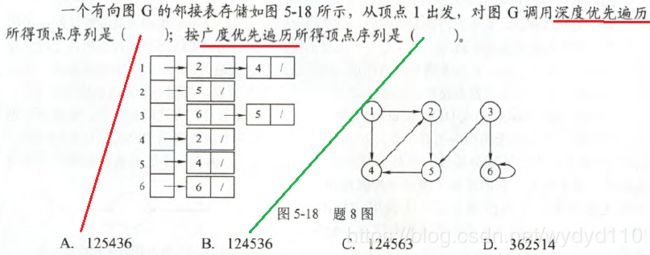
5、题图为一无向图,分别写出从顶点1出发,按深度优先搜索遍历算法得到的顶点序列,和按广度优先搜索遍历算法得到的顶点序列
解析
根据深度优先定义，先访问1，依次是2、3、4、5、6，注意是无向图。广度优先是一层一层访问，即123564，答案为123456 123564
答案： 123456 123564
其他课后题
1
2
解析：若一个无向图有n个顶点和n-1条边，可以使它连通但没有环（即生成树）。再加一条边，在不考虑重边的情况下，必然会构成环。
3
4（2011年计算机联考真题）
5
解析：
6（2009年计算机联考真题）
解析：
无向图的全部顶点的度之和等于边数的两倍。
7（2010年计算机联考真题）
解析：
图G的6个顶点构成一个完全无向图，边数为6*（6-5）/2=15
再加一条边后，第7个顶点必然与此完全无向图构成一个连通图，则边数最少为16
8
解析：
至少有多少个顶点，考虑此非连通图最极端的情况，即由一个完全无向图+一个顶点构成。
n个顶点构成边数为28的完全无向图：n(n-1)/2=28，n=8
8 + 1 = 9
9
10（2013年计算机联考真题）
设图的邻接矩阵A如下所示，各顶点的度依次是：
解析：
11
解析：
12
解析：
无向图的全部顶点的度数和 = 边数的两倍
4*5+3*4+2x = 23*2，解得x=7
13
解析：
14
解析：
5个顶点构成一个完全无向图，需要5（5-1）/2=10条边，再加一条边形成连通图。
15（2017年计算机联考真题）
16
解析：
17
18
解析：
19
解析：
20
21
22
23
24
25
26
27
解析：
28
解析：
29
解析：
30
解析：
无向图的邻接表：边表结点数 = 边数*2
31
解析：
有向图的邻接表：边数=边表结点数
32
解析：
33
解析：
34
35
36
解析：
37（以下下周完成）
解析：
38
解析：
图的遍历
40
解析：
41
解析：
42
43
解析：
44
解析：
45（2013计算机联考真题）
46（2016年计算机联考真题）
47
解析：
48
解析：
49
50（2010年计算机联考真题）
解析：
51（2015年计算机联考真题）
解析：
52（2010年计算机联考真题）
解析：
53
解析：
54
解析：
55
56（2012年计算机联考真题）
解析：
最小生成树的树形可能不唯一（可能存在权值相同的边），但代价一定是唯一的。
树的代价 = 树的全部边权值相加。
当最小生成树唯一时，即各边权值不同，Prim和Kruskal算法得到的最小生成树相同。
57
解析：
简单路径：路径序列中，顶点不重复出现的路径。
58
解析：
59（2012年计算机联考真题）
解析：
60（2016年计算机联考真题）
解析：
61
解析：
62（2016年计算机联考真题）
解析：
63
64
解析：
65
解析：
68（2012计算机联考真题）
解析：
69
解析：
70
解析：
71
解析：
72
解析：
关键路径：从源点到汇点具有最大长度的路径。
扩展：
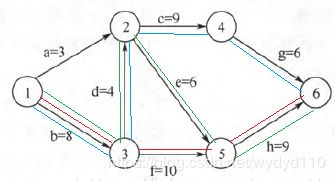
73（2013年计算机联考真题）
解析：
bdcg = 8+4+9+6 = 27
bdeh = 8+4+6+9 = 27
bfh = 8+10+9 = 27
74
解析：
75
解析：
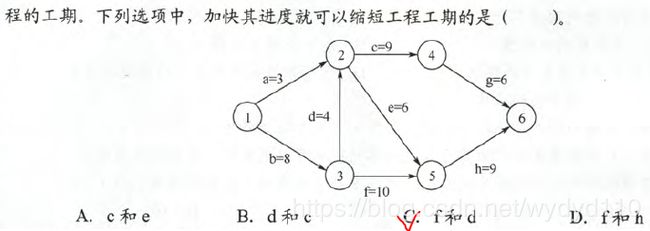
76（2012年计算机联考真题）
解析：
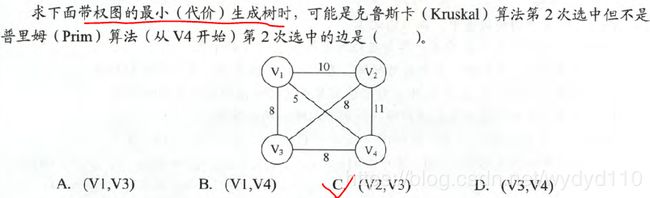
77（2015年计算机联考真题）
解析：
《Prim与Kruskal》
