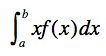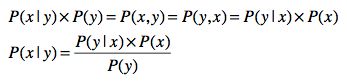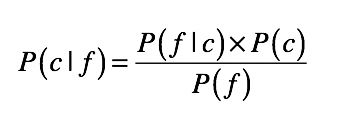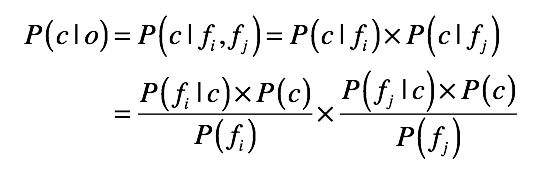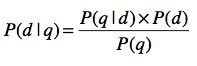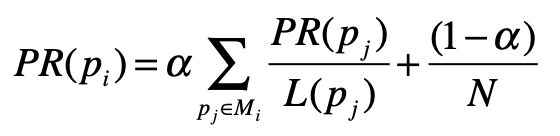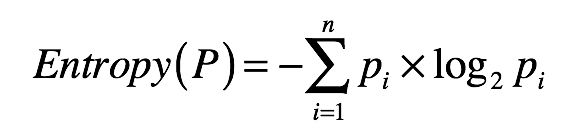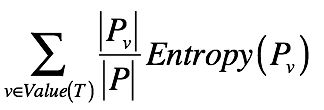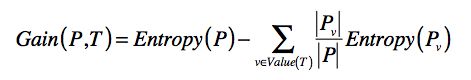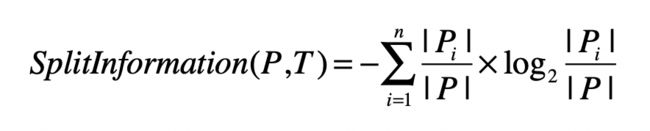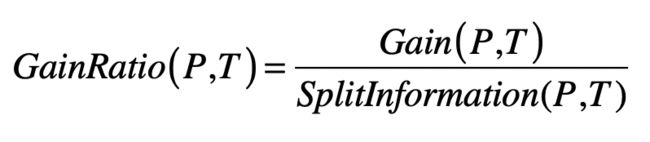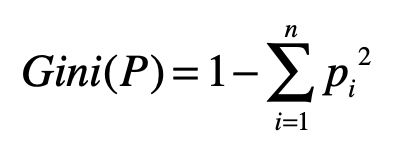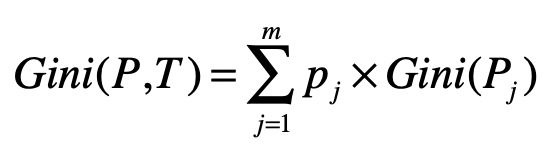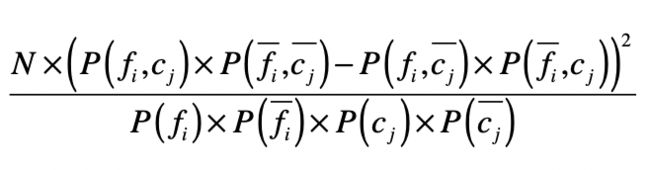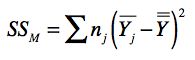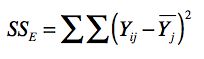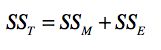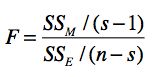数学之美2 - 概率篇

概率篇

• 朴素贝叶斯
• 文本分类
• 语言模型
• 马尔科夫模型
• 决策树
• A/B 测试

---

19 | 概率和统计：编程为什么需要概率和统计？

概率和统计里有哪些需要掌握的概念？

• 随机变量（Random Variable）来描述事件所有可能出现的状态
• 离散型随机变量（Discrete Random Variable）
• 连续型随机变量（Continuous Random Variable）
• 概率分布（Probability Distribution）来描述每个状态出现的可能性
• 联合概率（Joint Probability）
• 边缘概率（Marginal Probability）
• 条件概率

说了这么多，不知道你有没有一种感觉，其实概率论研究的就是这些概率之间相互转化的关系，比如联合概率、条件概率和边缘概率。通过这些关系，概率论中产生了著名的贝叶斯定理（Bayes’ theorem）。加上变量的独立性，我们就可以构建**朴素贝叶斯（Naive Bayes）**分类算法。

此外，基于概率发展而来的信息论，提出了很多重要的概率，例如**信息熵（Entropy）、香农熵（Shannon Entropy）、信息增益（Information Gain）、基尼指数（Gini）等。这些概念都被运用到了决策树（Decision Tree）**的算法中。

通过这些概念之间的相互推导，我们可以得到贝叶斯定理，这是朴素贝叶斯等系列算法的核心。而在概率基础之上发展而来的信息论，定义了信息熵、信息增益和基尼指数等，构成了决策树等系列算法的核心。

概率研究的是模型如何产生数据，统计研究的是如何通过数据来推导其背后的模型。所以说，概率和统计其实是互逆的。

概率和统计可以帮我们做什么？

• 第一，概率可以帮助我们进行更精准的复杂度分析；
• 第二，概率统计更多的是用在机器学习和大数据分析中；
• 第三，概率统计还可以用在各种机器学习的算法中。

---

20 | 概率基础（上）：一篇文章帮你理解随机变量、概率分布和期望值

离散 & 连续

随机变量根据其取值是否连续，可分为离散型随机变量和连续型随机变量。举几个例子，抛硬币出现正反面的次数以及每周下雨的天数，都是离散的值，所以对应的随机变量为离散型。而汽车每小时行驶的速度和银行排队的时间，都是连续的值，对应的随机变量为连续型。换句话，从计算的角度来说，我们可以直接求和得出的，就是“离散的”，需要用积分计算的，就是“连续的”。

概率分布

• 离散

抛硬币事件来看

离散分布模型：常用的离散分布有伯努利分布、分类分布、二项分布、泊松分布

• 连续

汽车每小时行驶的公里数

连续分布模型：比较经典的连续分布有正态分布、均匀分布、指数分布、拉普拉斯分布

期望值

期望值，也叫数学期望，是每次随机结果的出现概率乘以其结果的总和。如果我们把每种结果的概率看作权重，那么期望值就是所有结果的加权平均值。它在我们的生活中十分常见，例如计算多个数值的平均值，其实就是求期望值，只不过我们假设每个数值出现的概率是相同的。

在我看来，一个问题只要满足两个要素，我们就可以考虑使用期望值：

• 第一个要素，在这个问题中可能出现不同的情况，而且各种情况的出现满足了一定的概率分布；
• 第二个要素，每种情况都对应一个数值，这个数值代表了具体的应用含义。

那么，对于连续型的随机变量，这种期望值应该如何计算呢？我们需要使用下面的积分公式：

面积

---

21 | 概率基础（下）：联合概率、条件概率和贝叶斯法则，这些概率公式究竟能做什么？

联合概率、条件概率和边缘概率

解释清楚了条件概率，我就可以列出概率、条件概率和联合概率之间的“三角”关系了。简单的说，联合概率是条件概率和概率的乘积，采用通用的公式来表达就是：

贝叶斯定理

这就是非常经典的贝叶斯法则。为什么说经典呢？是因为它有很多应用的场景，比如朴素贝叶斯，你可以多多熟悉一下这个公式。在这个公式中，还包含了先验概率（Prior Probability）、似然函数（Likelihood）、边缘概率（Marginal Probability）和后验概率（Posterior Probability）的概念。

在这里面，我们把 P(x) 称为先验概率。之所以称为“先验”，是因为它是从数据资料统计得到的，不需要经过贝叶斯定理的推算。

P(y | x) 是给定 x 之后 y 出现的条件概率。在统计学中，我们也把 P(y | x) 写作似然函数 L(x | y)。在数学里，似然函数和概率是有区别的。概率是指已经知道模型的参数来预测结果，而似然函数是根据观测到的结果数据，来预估模型的参数。不过，当 y 值给定的时候，两者在数值上是相等的，在应用中我们可以不用细究。

另外，我们没有必要事先知道 P(y)。P(y) 可以通过联合概率 P(x, y) 计算边缘概率得来，而联合概率 P(x, y) 可以由 P(y|x) * P(x) 推出。针对离散型和连续型的边缘概率推导分别如下：

最主要的应用场景：通过先验概率，推导出后验概率，这就是贝叶斯定理神奇的地方。

随机变量之间的独立性

说到多个随机变量的联合和条件概率，你可能会产生一个问题：这些随机变量是否会相互影响呢？比如，性别和分数之间有怎样的关系？性别是否会影响分数的概率分布？

相互独立会产生一些有趣的现象，刚刚我们提到：

另外，将 p(x | y) = p(x) 带入贝叶斯公式，就可以得出：

---

22 | 朴素贝叶斯：如何让计算机学会自动分类？

例子

在开始正式的内容之前，我想问你一个问题，你是如何区分苹果、甜橙和西瓜的？

如何将原始信息转化为计算机能看懂的数据？

最常用的方式就是提取现实世界中的对象之属性，并将这些转化为数字。

朴素贝叶斯的核心思想

贝叶斯定理的核心思想：用先验概率和条件概率估计后验概率

那具体到这里的分类问题，我们该如何运用这个公式呢？为了便于理解，我们可以将上述公式改写成这样：

其中，c 表示一个分类（class），f 表示属性对应的数据字段（field）。如此一来，等号左边的 P(c|f) 就是待分类样本中，出现属性值 f 时，样本属于类别 c 的概率。而等号右边的 P(f|c) 是根据训练数据统计，得到分类 c 中出现属性 f 的概率。P©是分类 c 在训练数据中出现的概率，P(f) 是属性 f 在训练样本中出现的概率。

看到这里，你可能要问了，这里的贝叶斯公式只描述了单个属性值属于某个分类的概率，可是我们要分析的水果每个都有很多属性啊，这该怎么办呢？

别急，朴素贝叶斯在这里就要发挥作用了。这是基于一个简单假设建立的一种贝叶斯方法，并假定数据对象的不同属性对其归类影响时是相互独立的。此时若数据对象 o 中同时出现属性 fi 与 fj，则对象 o 属于类别 c 的概率就是这样：

对于出现的 0.00 概率，在做贝叶斯公式中的乘积计算时，会出现结果为 0 的情况，因此我们通常取一个比这个数据集里最小统计概率还要小的极小值，来代替“零概率”。比如，我们这里取 0.01。在填充训练数据中从来没有出现过的属性值的时候，我们就会使用这种技巧，我们给这种技巧起个名字就叫作平滑（Smoothing）。

你可能已经注意到了，这几个公式里的概率乘积通常都非常小，在物品的属性非常多的时候，这个乘积可能就小到计算机无法处理的地步。因此，在实际运用中，我们还会采用一些数学手法进行转换（比如取 log 将小数转换为绝对值大于 1 的负数），原理都是一样的。

内容比较多，我稍微总结一下。朴素贝叶斯分类主要包括这几个步骤：

• 准备数据：针对水果分类这个案例，我们收集了若干水果的实例，并从水果的常见属性入手，将其转化为计算机所能理解的数据。这种数据也被称为训练样本。
• 建立模型：通过手头上水果的实例，我们让计算机统计每种水果、属性出现的先验概率，以及在某个水果分类下某种属性出现的条件概率。这个过程也被称为基于样本的训练。
• 分类新数据：对于一颗新水果的属性数据，计算机根据已经建立的模型进行推导计算，得到该水果属于每个分类的概率，实现了分类的目的。这个过程也被称为预测。

朴素贝叶斯分类 VS 其他分类算法

• 和KNN 最近邻相比，朴素贝叶斯需要更多的时间进行模型的训练，但是它在对新的数据进行分类预测的时候，通常效果更好、用时更短。
• 和决策树相比，朴素贝叶斯并不能提供一套易于人类理解的规则，但是它可以提供决策树通常无法支持的模糊分类（一个对象可以属于多个分类）。
• 和SVM 支持向量机相比，朴素贝叶斯无法直接支持连续值的输入。所以，在前面的案例中，我将连续值转化成了离散值，便于朴素贝叶斯进行处理。

应用场景

如果一个分类的应用场景中，待分类对象的属性值大部分都是离散的（或者很容易转化为离散的）、需要支持模糊分类，并且需要快速可靠的实时分类，那么这种场景通常就非常适合使用朴素贝叶斯方法。

---

23 | 文本分类：如何区分特定类型的新闻？

文本分类系统的基本框架

基于自然语言的预处理

和之前的水果案例相比，新闻这种文本数据最大的区别在于，它包含了大量的自然语言。那么如何让计算机理解自然语言呢？我们的计算机体系没有思维，要理解人类的语言在现阶段是不现实的。但是，我们仍然可以对自然语言进行适当的处理，将其变为机器所能处理的数据。

首先，我们要知道，文本的的重要属性是什么，这样我们才能提取出它的特征。怎么才能知道哪些属性是重要的呢？

我举个例子，假如说，有人给你一篇几千字的文章，让你在 10 秒钟之内说出文章大意，你会怎么办？我想大部分人的解决方案是“找关键词”！没错，我们也可以交给计算机用同样的办法。而计算机处理文本的基本单位就是字和单词，这就是人们最常用的方法：词袋（Bag of words）模型。

这种模型会忽略文本中的词语出现的顺序以及相应的语法，将整篇文章仅仅看做是一个大量单词的组合。文本中每个词的出现都是独立的，不依赖于其他词的出现情况。讲到这里，你有没有发现在词包模型中，所有单词相互之间是独立的，这个假设和朴素贝叶斯模型的独立假设是不是一致呀？

没错！这里我们就可以很巧妙地将朴素贝叶斯和文本处理结合起来了。不过先不要急，我们还要掌握一些方法，才能将文本中的长篇大论处理成关键词。

• 分词

介绍两种目前比较主流的分词模型，你只需要了解就行。

第一种是基于字符串匹配。其实就是扫描字符串。如果发现字符串的子串和词相同，就算匹配成功。匹配规则通常是“正向最大匹配”“逆向最大匹配”“长词优先”。这些算法的优点是只需使用基于字典的匹配，因此计算复杂度低；缺点是处理歧义词效果不佳。

第二种是基于统计和机器学习。这类分词基于人工标注的词性和统计特征，对中文进行建模。训练阶段，根据标注好的语料对模型参数进行估计。 在分词阶段再通过模型计算各种分词出现的概率，将概率最大的分词作为最终结果。常见的序列标注模型有隐马尔科夫模型（HMM，Hidden Markov Model）和条件随机场（CRF，Conditional Random Field），我们后面章节会讲到，这里我先不展开。

• 取词干和归一化

我们刚才说了，相对中文而言，英文完全不需要考虑分词。不过它也有中文不具有的单复数、各种时态，因此它需要考虑取词干（stemming）。取词干的目标就是为了减少词的变化形式，将派生词转化为基本形式。

最后，我们还要考虑大小写转化和多种拼写（例如 color 和 colour）这样的统一化，我们把这种做法称为归一化。

• 停用词

无论何种语言，都会存在一些不影响（或基本不影响）相关性的词。有的时候干脆可以指定一个叫停用词（stop word）的字典，直接将这些词过滤，不予以考虑。例如英文中的 a、an、the、that、is、good、bad 等。中文“的、个、你、我、他、好、坏”等。

如此一来，我们可以在基本不损失语义的情况下，减少数据文件的大小，提高计算机处理的效率。当然，也要注意停用词的使用场景，例如用户观点分析，good 和 bad 这样的形容词反而成为了关键。不仅不能过滤，反而要加大它们的权重。

• 同义词和扩展词

不同的地域或者不同时代，会导致人们对于同样的物品叫法也不同。例如，在中国北方“番茄“应该叫“西红柿”，而台湾地区将“菠萝”称为“凤梨”。对于计算机而言，需要意识到这两个词是等价的。添加同义词就是一个很好的手段。

有了这样的词典，当看到文本中出现“番茄”关键词的时候，计算机系统就会将其等同于“西红柿”这个词。有的时候我们还需要扩展词。如果简单地将 Dove 分别和多芬、德芙简单地等价，那么多芬和德芙这两个完全不同的品牌也变成了同义词，这样做明显是有问题的。那么我们可以采用扩展关系，当系统看到文本中的“多芬”时将其等同于“Dove”，看到“德芙”时将其等同于“Dove”。但是看到“Dove”的时候并不将其等同于“多芬”或“德芙”。

通过词包模型的假设，以及上述这些自然语言处理的方法，我们可以将整篇的文字，切分为一个个的单词，这些是表示文章的关键属性。你不难发现，每个单词可以作为文章的属性，而通过这些单词的词频（出现的频率），我们很容易进行概率的统计。下面我对分类的先验概率、单词的先验概率、某个分类下某个单词的条件概率分别给出了示例。

如果发现某些单词从未在某个分类中出现，例如“航母”这个词从未在“体育”和“娱乐”这两个分类中出现。对于这种情况，我们可以使用平滑（smoothing）的技术，将其词频或条件概率设置为一个极小的值。这里，我设置了最小的词频，也就是 1。

运用朴素贝叶斯模型

在新闻分类中，o 就表示一篇文章，而c表示新闻的种类（包括政治、军事、财经等等）。而属性字段f就是我们从文档集而建立的各种单词。公式等号左边的 P(c|f) 就是待分类新闻中，出现单词 f 时，该新闻属于类别 c 的概率。而等号右边的 P(f|c) 是根据训练数据统计，得到分类 c 中出现单词 f 的概率。P( c ) 是分类 c 在新闻训练数据中出现的概率，P(f) 是单词 f 在训练样本中出现的概率。

这里需要注意一个很实际的问题：文章的篇幅很长，常常会导致非常多的 P(f|c) 连续乘积。而 P(f|c) 通常是非常小的数值，因此最后的乘积将快速趋近于 0 以至于计算机无法识别。这里可以使用我们之前提到的一些数学手法进行转换，比如取 log，将小数转换为绝对值大于 1 的负数。这样的转换，虽然会改变每篇文章属于每个分类的概率之绝对值，但是并不会改变这些概率的相对大小。

总结

在这一讲中，我讲了一个文本分类系统的几个关键步骤，其中最重要的是自然语言的处理和分类模型的训练和预测。

自然语言的处理是关键的预处理步骤，它将文本转换成计算机所能处理的数据。常见方法包括中文分词，英文的取词干和归一化，还有适用于各种语言的停用词、同义词和扩展词等。如果不考虑这些词出现的先后顺序，以及表达的深层次语义，那么我们就可以使用词包的方法，将大段的文章和语句转化成单词所组成的集合。之后，我们就能统计每个单词属于每个分类的条件概率，以及分类和单词的先验概率。

一旦将文章表示为单词的集合，我们就会发现，朴素贝叶斯的模型非常适合文章的分类。因为所有单词出现的词频都是离散值，非常适合统计概率。此外，许多新闻之类的文章本身也是跨了多个领域，因此有可能属于多个分类，朴素贝叶斯也能支持这点。我们针对“中国航母”这个短语进行了测试，发现其属于“政治”和“军事”分类的可能性最高。不过要注意的是，文章可能包含非常多的单词，朴素贝叶斯模型中的连续乘积会导致过小的值，甚至计算机都无法处理。为了避免这种情况，我们可以使用 log 的数学变换。

---

24 | 语言模型：如何使用链式法则和马尔科夫假设简化概率模型？

语言模型是什么？

• 链式法则

链式法则是概率论中一个常用法则。它使用一系列条件概念率和边缘概率，来推导联合概率，我用一个公式来给你看看它的具体表现形式。

其中，x1 到 xn 表示了 n 个随机变量。

• 马尔科夫假设

理解了链式法则，我们再来看看马尔可夫假设。这个假设的内容是：任何一个词 wi 出现的概率只和它前面的 1 个或若干个词有关。基于这个假设，我们可以提出多元文法（Ngram）模型。Ngram 中的“N”很重要，它表示任何一个词出现的概率，只和它前面的 N-1 个词有关。

我以二元文法模型为例，来给你解释。按照刚才的说法，二元文法表示，某个单词出现的概率只和它前面的 1 个单词有关。也就是说，即使某个单词出现在一个很长的句子中，我们也只需要看前面那 1 个单词。用公式来表示出来就是这样：

如果是三元文法，就说明某个单词出现的概率只和它前面的 2 个单词有关。即使某个单词出现在很长的一个句子中，它也只看相邻的前 2 个单词。用公式来表达就是这样：

你也许会好奇，那么一元文法呢？按照字面的意思，就是每个单词出现的概率和前面 0 个单词有关。这其实说明，每个词的出现都是相互独立的。用公式来表达就是这样的：

弄明白链式法则和马尔科夫假设之后，我们现在来看语言模型。

如何解决 0 概率和高复杂度的问题呢？马尔科夫假设和多元文法模型能帮上大忙了。如果我们使用三元文法模型，上述公式可以改写为：

语言模型的应用

• 机器翻译
• 语音识别
• 中文分词
• 信息检索

信息检索

信息检索很关心的一个问题就是相关性，也就是说，给定一个查询，哪篇文档是更相关的呢？为了解决相关性问题，布尔模型和向量空间检索模型都是从查询的角度出发，观察查询和文档之间的相似程度，并以此来决定如何找出相关的文档。这里的“相似程度”，你可以理解为查询和文档长得有多像。那么，语言模型如何来刻画查询和文档之间的相关度呢？

通过我们手头的文档集合，并不能直接获得 P(d|q)。好在我们已经学习过了贝叶斯定理，通过这个定理，我们可以将 P(d|q) 重写如下：

而语言模型，为我们解决了如何计算 P(q|d) 的问题，让 k1,k2,…,kn 表示查询 q 里包含的 n 个关键词。那么根据之前的链式法则公式，可以重写为这样：

为了提升效率，我们也使用马尔科夫假设和多元文法。假设是三元文法，那么我们可以写成这样：

最终，当用户输入一个查询 q 之后，对于每一篇文档 d，我们都能获得 P(d|q) 的值。根据每篇文档所获得的 P(d|q) 这个值，由高到低对所有的文档进行排序。这就是语言模型在信息检索中的常见用法。

中文分词

多种分词

产生歧义

那么这种情况下，语言模型能为我们做什么呢？我们知道，语言模型是基于大量的语料来统计的，所以我们可以使用这个模型来估算，哪种情况更合理。

假设整个文档集合是 D，要分词的句子是 s，分词结果为 w1, … wn，那么我们可以求 P(s) 的概率为：

请注意，在信息检索中，我们关心的是每篇文章产生一个句子（也就是查询）的概率，而这里可以是整个文档集合 D 产生一个句子的概率。

根据链式法则和三元文法模型，那么上面的式子可以重写为：

也就是说，语言模型可以帮我们估计某种分词结果，在文档集合中出现的概率。但是由于不同的分词方法，会导致 w1 到 wn 的不同，因此就会产生不同的 P(s)。接下来，我们只要取最大的 P(s)，并假设这种分词方式是最合理的，就可以在一定程度上解决歧义。我们可以使用这个公式来求解：

其中，Wi 表示第 i 种分词方法。

小结

• 第一，使用联合概率，条件概率和边缘概率的“三角”关系，进行相互推导。链式法则就是很好的体现。
• 第二，使用马尔科夫假设，把受较多随机变量影响的条件概率，简化为受较少随机变量影响的条件概率，甚至是边缘概率。
• 第三，使用贝叶斯定理，通过先验概率推导后验概率。在信息检索中，给定查询的情况下推导文档的概率，就需要用到这个定理。

---

25 | 马尔科夫模型：从PageRank到语音识别，背后是什么模型在支撑？

马尔科夫模型

在介绍语言模型的时候，我们提到了马尔科夫假设，这个假设是说，每个词出现的概率和之前的一个或若干个词有关。我们换个角度思考就是，每个词按照一定的概率转移到下一个词。怎么个转移呢？我来解释一下。如果把词抽象为一个状态，那么我们就可以认为，状态到状态之间是有关联的。前一个状态有一定的概率可以转移到到下一个状态。如果多个状态之间的随机转移满足马尔科夫假设，那么这类随机过程就是一个马尔科夫随机过程。而刻画这类随机过程的统计模型，就是马尔科夫模型（Markov Model）。

前面讲多元文法的时候，我提到了二元文法、三元文法。对于二元文法来说，某个词出现的概率只和前一个词有关。对应的，在马尔科夫模型中，如果一个状态出现的概率只和前一个状态有关，那么我们称它为一阶马尔科夫模型或者马尔科夫链。对应于三元、四元甚至更多元的文法，我们也有二阶、三阶等马尔科夫模型。

• 马尔科夫模型 - 马尔科夫链

• PageRank 链接分析算法

Google 公司最引以为傲的 PageRank 链接分析算法，它的核心思想就是基于马尔科夫链。这个算法假设了一个“随机冲浪者”模型，冲浪者从某张网页出发，根据 Web 图中的链接关系随机访问。在每个步骤中，冲浪者都会从当前网页的链出网页中随机选取一张作为下一步访问的目标。在整个 Web 图中，绝大部分网页节点都会有链入和链出。那么冲浪者就可以永不停歇地冲浪，持续在图中走下去。

在随机访问的过程中，越是被频繁访问的链接，越是重要。可以看出，每个节点的 PageRank 值取决于 Web 图的链接结构。假如一个页面节点有很多的链入链接，或者是链入的网页有较高的被访问率，那么它也将会有更高的被访问概率。

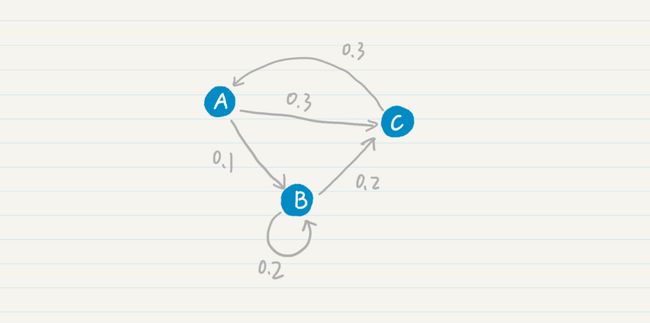
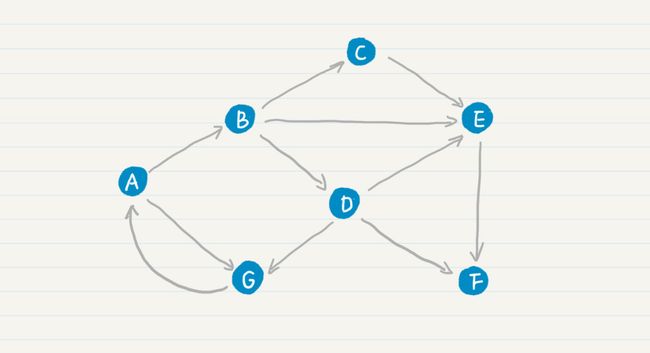
那么，PageRank 的公式和马尔科夫链有什么关系呢？我先给你看一张 Web 的拓扑图。

其中 A、B、C 等结点分别代表了页面，而结点之间的有向边代表了页面之间的超链接。看了这张图中，你是不是觉得 Web 拓扑图和马尔科夫链的模型图基本上是一致的？我们可以假设每张网页就是一个状态，而网页之间的链接表明了状态转移的方向。这样，我们很自然地就可以使用马尔科夫链来刻画“随机冲浪者”。

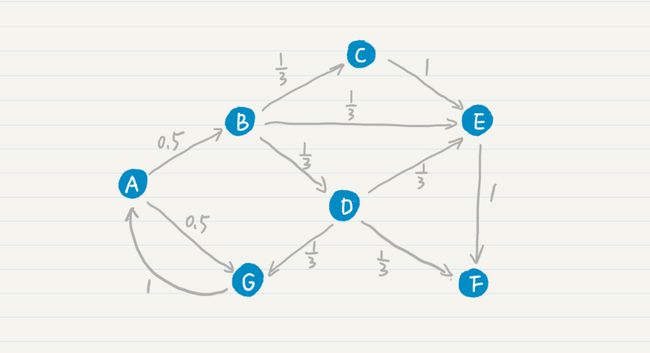
另外，在最基本的 PageRank 算法中，我们可以假设每张网页的出度是 n，那么从这张网页转移到任何下一张相连网页的概率都是 1/n ，因此这个转移的概率只和当前页面有关，满足一阶马尔科夫模型的假设。我在之前的拓扑结构中添加了转移的概率。

PageRank 在标准的马尔科夫链上，引入了随机的跳转操作，也就是假设冲浪者不按照 Web 图的拓扑结构走下去，只是随机挑选了一张网页进行跳转。这样的处理是类比人们打开一张新网页的行为，也是符合实际情况的，避免了信息孤岛的形成。最终，根据马尔科夫链的状态转移和随机跳转，可以得到如下的 PageRank 公式。

其中，pi 表示第 i 张网页，Mi 是 pi 的入链接集合，pj 是 Mi 集合中的第 j 张网页。PR(pj) 表示网页 pj 的 PageRank 得分，L(pj)表示网页 pj 的出链接数量，1/L(pj) 就表示从网页 pj 跳转到 pi 的概率。α 是用户不进行随机跳转的概率，N 表示所有网页的数量。

从最简单的马尔科夫链，到多阶的马尔科夫模型，它们都可以刻画基于马尔科夫假设的随机过程，例如概率语言模型中的多元文法和 PageRank 这类链接分析算法。但是，这些模型都是假设每个状态对我们都是已知的，比如在概率语言模型中，一个状态对应了单词“上学”，另一个状态对应了单词“书包”。可是，有没有可能某些状态我们是未知的呢？下面我们就来详细说说这种情况。

隐马尔科夫模型

在某些现实的应用场景中，我们是无法确定马尔科夫过程中某个状态的取值的。这种情况下，最经典的案例就是语音识别。使用概率对语音进行识别的过程，和语言模型类似，因此我们可以把每个等待识别的词对应为马尔科夫过程中的一个状态。不过，语音识别所面临的困难更大。为什么呢？你先看看下面这个句子。这个句子里全都是拼音，你能看出它表示什么意思吗？

总结

马尔科夫模型考虑了 n 个状态之间的转移及其对应的关系。这个状态是比较抽象的含义，在不同的应用领域代表不同的含义。在概率语言模型中，状态表示不同的词，状态之间的转移就代表了词按照一定的先后顺序出现。在 PageRank 这种链接分析中，状态表示不同的网页，状态之间的转移就代表了人们在不同网页之间的跳转。

在马尔科夫模型中，我们知道了每种状态及其之间转移的概率，然后求解序列出现的概率。然而，有些现实的场景更为复杂，比如说我们观测到的不是状态本身，而是状态按照一定概率分布所产生的输出。针对这种情况，隐马尔科夫模型提出了一种两层的模型，同时考虑了状态之间转移的概率和状态产生输出的概率，为语音识别、手写识别、机器翻译等提供了可行的解决方案。

隐马尔科夫模型需要回答的最主要问题是：给定一个模型和某个特定的输出序列，如何找到最可能产生这个输出的状态序列？在本节中，我使用了“项目开发时间”这个例子展示隐马尔科夫模型是如何工作的。不过这个例子很简单，我只比较了两种可能性。但是，实际中可能性是非常多的，如果我们使用穷举法，那么复杂度一定很高。

我们可以把两层的模型看作图结构。其中，状态和输出是结点，转移和输出关系是边，相应的概率是边的权重，这个时候我们就可以对 Dijkstra 算法稍加修改，来找出权重乘积最大的最优路径，提升查找的效率。我们还可以利用状态序列之间存在的先后关系，使用基于动态规划的维特比（Viterbi）算法来找出最优路径。

回顾 PageRank 链接分析算法

PageRank 是基于马尔科夫链的。它假设了一个“随机冲浪者”模型，冲浪者从某张网页出发，根据 Web 图中的链接关系随机访问。在每个步骤中，冲浪者都会从当前网页的链出网页中，随机选取一张作为下一步访问的目标。此外，PageRank 还引入了随机的跳转操作，这意味着冲浪者不是按 Web 图的拓扑结构走下去，只是随机挑选了一张网页进行跳转。

基于之前的假设，PageRank 的公式定义如下：

其中，pi 表示第 i 张网页，Mi 是 pi 的入链接集合，pj 是 Mi 集合中的第 j 张网页。PR(pj) 表示网页 pj 的 PageRank 得分，L(pj)表示网页 pj 的出链接数量，1/L(pj) 就表示从网页 pj 跳转到 pi 的概率。α 是用户不进行随机跳转的概率，N 表示所有网页的数量。

PageRank 的计算是采样迭代法实现的：一开始所有网页结点的初始 PageRank 值都可以设置为某个相同的数，例如 1，然后我们通过上面这个公式，得到每个结点新的 PageRank 值。每当一张网页的 PageRank 发生了改变，它也会影响它的出链接所指向的网页，因此我们可以再次使用这个公式，循环地修正每个网页结点的值。由于这是一个马尔科夫过程，所以我们能从理论上证明，所有网页的 PageRank 最终会达到一个稳定的数值。整个证明过程很复杂，这里我们只需要知道这个迭代计算的过程就行了。

简化 PageRank 公式

那么，这个计算公式和矩阵操作又有什么联系呢？为了把问题简化，我们暂时不考虑随机跳转的情况，而只考虑用户按照网页间链接进行随机冲浪。那么 PageRank 的公式就简化为：

我们再来对比看看矩阵点乘的计算公式。

以上两个公式在形式上是基本一致的。因此，我们可以把 Σ(PR(pj)/L(pj)) 的计算，分解为两个矩阵的点乘。一个矩阵是当前每张网页的 PageRank 得分，另一个矩阵就是邻接矩阵。所谓邻接矩阵，其实就是表示图结点相邻关系的矩阵。

考虑随机跳转

我们把 Σ(PR(pj)/L(pj)) 部分用 A 表示，那么完整的 PageRank 公式就可以表示为：

于是，我们可以把上述公式分解为如下两个矩阵的点乘：

我们前面提到，PageRank 算法需要迭代式计算。为了避免计算后的数值越来越大甚至溢出，我们可以进行归一化处理，保证所有结点的数值之和为 1。

接下来，我们只需要再重复之前的步骤，直到每个结点的值趋于稳定就可以了。

使用 Python 进行实现

说到这里，我已经把如何把整个 PageRank 的计算，转换成多个矩阵的点乘这个过程讲完了。这样一来，我们就可以利用 Python 等科学计算语言提供的库，来完成基于 PageRank 的链接分析。

总结

我们可以把向量看作一维数组，把矩阵看作二维数组。矩阵的点乘，是由若干个向量的点乘组成的，所以我们可以通过矩阵的点乘操作，挖掘多组向量两两之间的关系。

今天我们讲了矩阵的点乘操作在 PageRank 算法中的应用。通过表示网页的邻接二元关系，我们可以使用矩阵来计算 PageRank 的得分。在这个应用场景下，矩阵点乘体现了多个马尔科夫过程中的状态转移。

矩阵点乘和其他运算操作，还可以运用在很多其他的领域。例如，我在上一节介绍 K 均值聚类算法时，就提到了需要计算某个数据点向量、其他数据点向量之间的距离或者相似度，以及使用多个数据点向量的平均值来获得质心点的向量，这些都可以通过矩阵操作来完成。

另外，在协同过滤的推荐中，我们可以使用矩阵点乘，来实现多个用户或者物品之间的相似程度，以及聚集后的相似程度所导致的最终推荐结果。

---

26 | 信息熵：如何通过几个问题，测出你对应的武侠人物？

例子

问卷调查

• 测测你是哪个武侠人物
• 测星座
• 测运势

这种心理或者性格测试的题目是怎么设计的吗？

什么是信息熵？

• 随机变量

x

• 概率

P(x) 表示 x 出现的概率

• 信息量

H(x)=−log(P(x))

信息量是信息论中的一个度量，简单来说就是，当我们观察到某个随机变量的具体值时，接收到了多少信息。

而我们接收到的信息量跟发生事件的概率有关。事情发生的概率越大，产生的信息量越小；事情发生的概率越小，产生的信息量越大。

• 熵（混乱度）

某个随机变量的信息量之期望。

从集合和分组的角度来说，如果一个集合里的元素趋向于落在同一分组里，那么告诉你某个元素属于哪个分组的信息量就越小，整个集合的熵也越小，换句话说，整个集合就越“纯净”。相反，如果一个集合里的元素趋向于分散在不同分组里，那么告诉你某个元素属于哪个分组的信息量就越大，整个集合的熵也越大，换句话说，整个集合就越“混乱”。

一个集合中所包含的分组越多、元素在这些分组里分布得越均匀，熵值也越大。而熵值表示了纯净的程度，或者从相反的角度来说，是混乱的程度。

• 多个小集合的整体的熵

好了，你已经知道单个集合的熵是如何计算的了。那么，如果将一个集合划分成多个更小的集合之后，又该如何根据这些小集合，来计算整体的熵呢？之前我们提到了信息量和熵具有加和的性质，所以对于包含多个集合的更大集合，它的信息量期望值是可以通过每个小集合的信息量期望值来推算的。具体来说，我们可以使用如下公式：

其中，T 表示一种划分，Pv 表示划分后其中某个小集合，Entropy(Pv)表示某个小集合的熵， 而 |Pv|/|P| 表示某个小集合出现的概率。所以这个公式其实就表示，对于多个小集合而言，其整体的熵等于各个小集合之熵的加权平均。而每个小集合的权重是其在整体中出现的概率。

什么是信息增益？（区分能力）

如果我们将划分前后的整体熵做个对比，你会发现划分后的整体熵要小于划分之前的整体熵。这是因为每次划分，都可能将不同分组的元素区分开来，降低划分后每个小集合的混乱程度，也就是降低它们的熵。我们将划分后整体熵的下降，称为信息增益（Information Gain）。如果划分后整体熵下降的越多，信息增益就越大。我列出公式便于你的理解。

其中 T 表示当前选择的特征，Entropy§ 表示选择特征 T 之前的熵，Entropy(Pv)表示特征 T 取值为 v 分组的熵。减号后面的部分表示选择 T 做决策之后，各种取值加权平均后整体的熵。Gain(P,T) 表示两个熵值之差，越大表示信息增益越多，应该选择这维特征 T。

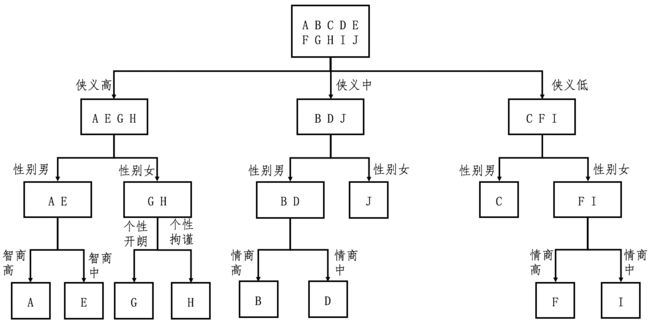
我们把这个概念放到咱们的小游戏里就是，如果一个测试问题能够将来自不同分组的人物尽量的分开，也就是该划分对应的信息增益越高，那么我们就认为其区分能力越高，提供的信息含量也越多。好，说到这里，让我们从游戏的最开始出发，比较一下有关性别和智商的两个测试题。

信息增益和信息熵是紧密相关的。如果说信息熵衡量了某个状态下，每个分组的纯净程度或者说混乱程度，那么信息增益就是比较了不同状态下，信息熵的差异程度。

总结

这一讲中，我们从一个有趣的人物性格测试开始，探讨了如何高效率地进行问卷调查。其中主要包含了两个要点：信息熵和信息增益。熵的计算是基于集合内各组元素分布的概率来进行的。而信息增益是集合划分前后整体熵的差值。对某个集合进行划分，都会将其中元素细分到更小的集合，而每个细分的集合纯净度就会提高，整体熵就会下降，其中下降的部分就是信息增益。

了解信息熵和信息增益的定义之后，我们可以用它们来安排测试问题的先后顺序。其核心的思路是，利用信息增益找出区分力最强的测试题。如果一道测试题可以将来自不同分组的元素分隔开来，那么就说它是有区分力的。如果分隔后，每个细分的集合其熵越趋近于 0，那么我们说这个测试题的区分力越强。

---

27 | 决策树：信息增益、增益比率和基尼指数的运用

如何通过信息熵挑选合适的问题？

为了实现一个更简短的问卷，你也许很自然地就想到，每次选择问题的时候，我们可以选择信息增益最高的问题，这样熵值下降得就最快。这的确是个很好的方法。我们来试一试。

从这个图可以看出来，对于每种人物的判断，我们至多需要问 3 个问题，没有必要问全 5 个问题。比如，对于人物 J 和 C，我们只需要问 2 个问题。假设读者属于 10 种武侠人物的概率是均等的，那么我们就可以利用之前介绍的知识，来计算读者需要回答的问题数量之期望值。每种人物出现的概率是 0.1，8 种人物需要问 3 个问题，2 种人物需要问 2 个问题，那么回答问题数的期望值是 0.8 * 3 + 0.2 * 2 = 2.8（题）。

好了，现在我们总结一下，如何才能进行高效的问卷调查。最核心的思想是，根据当前的概率分布，挑选在当前阶段区分能力更强的那些问题。具体的步骤有三个。

• 第一步，根据分组中的人物类型，为每个集合计算信息熵，并通过全部集合的熵之加权平均，获得整个数据集的熵。注意，一开始集合只有一个，并且包含了所有的武侠人物。
• 第二步，根据信息增益，计算每个问卷题的区分能力。挑选区分能力最强的题目，并对每个集合进行更细的划分。
• 第三步，有了新的划分之后，回到第一步，重复第一和第二步，直到没有更多的问卷题，或者所有的人物类型都已经被区分开来。这一步也体现了递归的思想。

其实，上述这个过程就体现了训练决策树（Decision Tree）的基本思想。决策树学习属于归纳推理算法之一，适用于分类问题。在前面介绍朴素贝叶斯的时候，我说过，分类算法主要包括了建立模型和分类新数据两个阶段。决定问卷题出现顺序的这个过程，其实就是建立决策树模型的过程。

ID3

随着机器学习的快速发展，人们也提出了不少优化版的决策树。采用信息增益来构建决策树的算法被称为ID3（Iterative Dichotomiser 3，迭代二叉树 3 代）。但是这个算法有一个缺点，它一般会优先考虑具有较多取值的特征，因为取值多的特征会有相对较大的信息增益。这是为什么呢？

C4.5 算法

你仔细观察一下信息熵的定义，就能发现背后的原因。更多的取值会把数据样本划分为更多更小的分组，这样熵就会大幅降低，信息增益就会大幅上升。但是这样构建出来的树，很容易导致机器学习中的过拟合现象，不利于决策树对新数据的预测。为了克服这个问题，人们又提出了一个改进版，C4.5 算法。

这个算法使用信息增益率（Information Gain Ratio）来替代信息增益，作为选择特征的标准，并降低决策树过拟合的程度。信息增益率通过引入一个被称作分裂信息（Split Information）的项来惩罚取值较多的特征，我把相应的公式给你列出来了。

其中，训练数据集 P 通过属性 T 的属性值，划分为 n 个子数据集，|Pi| 表示第 i 个子数据集中样本的数量，|P| 表示划分之前数据集中样本总数量。 这个公式看上去和熵很类似，其实并不相同。

熵计算的时候考虑的是，集合内数据是否属于同一个类，因此即使集合数量很多，但是集合内的数据如果都是来自相同的分类（或分组），那么熵还是会很低。而这里的分裂信息是不同的，它只考虑子集的数量。如果某个特征取值很多，那么相对应的子集数量就越多，最终分裂信息的值就会越大。正是因为如此，人们可以使用分裂信息来惩罚取值很多的特征。具体的计算公式如下：

其中 Gain(P,T)是数据集 P 使用特征 T 之后的信息增益，GainRatio(P,T) 是数据集 P 使用特征 T 之后的信息增益率。

CART 算法

另一种常见的决策树是 CART 算法（Classification and Regression Trees，分类与回归树）。这种算法和 ID3、C4.5 相比，主要有两处不同：

• 在分类时，CART 不再采用信息增益或信息增益率，而是采用基尼指数（Gini）来选择最好的特征并进行数据的划分；
• 在 ID3 和 C4.5 决策树中，算法根据特征的属性值划分数据，可能会划分出多个组。而 CART 算法采用了二叉树，每次把数据切成两份，分别进入左子树、右子树。

当然，CART 算法和 ID3、C4.5 也有类似的地方。首先，CART 中每一次迭代都会降低基尼指数，这类似于 ID3、C4.5 降低信息熵的过程。另外，基尼指数描述的也是纯度，与信息熵的含义相似。我们可以用下面这个公式来计算每个集合的纯度。

其中，n 为集合 P 中所包含的不同分组（或分类）数量。如果集合 P 中所包含的不同分组越多，那么这个集合的基尼指数越高，纯度越低。

然后，我们需要计算整个数据集的基尼指数。

其中，m 为全集使用特征 T 划分后，所形成的子集数量。Pj 为第 j 个集合。

无论是何种决策树算法，来自信息论的几个重要概念：信息熵、信息增益、信息增益率、基尼指数都起到了重要的作用。如果你能很好的学习并运用这些概念，那么决策树这种类型的算法就不难理解了。

小结

通过这两节的介绍，我想你对信息熵、信息增益、基尼指数等信息论的概念，以及基于这些概念的决策树分类算法应该有了一定了解。决策树算法的优势在于，容易理解和实现。此外，对于通过样本训练所得的树结构，其每个结点都是基于某个数据特征的判定，对于我们的阅读和解释来说都是很方便的。

当然，决策树也有不足。之前我已经提到，这类算法受训练样本的影响很大，比较容易过拟合。在预测阶段，如果新的数据和原来的训练样本差异较大，那么分类效果就会比较差。为此人们也提出了一些优化方案，比如剪枝和随机森林。

---

28 | 熵、信息增益和卡方：如何寻找关键特征？

特征选择：

• 信息熵
• 卡方检验

什么是特征选择？

在编程领域中，机器学习已经有了十分广泛的应用，它主要包括监督式学习（Supervised Learning）和非监督式的学习（Unsupervised Learning）。监督式学习，是指通过训练资料学习并建立一个模型，并依此模型推测新的实例，主要包括分类（Classification）和回归（Regression）。

“特征”（Feature），是机器学习非常常用的术语，它其实就是可用于模型拟合的各种数据。前面讲朴素贝叶斯分类时，我解释了如何把现实世界中水果的各类特征转化为计算机所能理解的数据，这个过程其实就是最初级的特征工程。当然，特征工程远不止原始特征到计算机数据的转化，还包括特征选择、缺失值的填补和异常值的去除等等。这其中非常重要的一步就是特征选择。

利用信息熵进行特征选择

那么，我们怎么能知道哪些特征是更重要的呢？对于分类问题，我们更关心的是如何正确地把一篇文章划分到正确的分类中。一个好的特征选择，应该可以把那些对分类有价值的信息提取出来，而过滤掉那些对分类没有什么价值的信息。既然如此，我们能不能充分利用分类标签来进行挑选呢？答案是肯定的。前两节，我描述了信息熵和信息增益的工作原理。这里，我就可以使用它们来进行特征选择。

如果一个特征，经常只在某个或少数几个分类中出现，而很少在其他分类中出现，那么说明这个特征具有较强的区分力，它的出现很可能预示着整个数据属于某个分类的概率很高或很低。

这个时候，对于一个特征，我们可以看看包含这个特征的数据，是不是只属于少数几个类。举个例子，出现“电影”这个词的文章，经常出现在“娱乐”这个分类中，而很少出现在“军事”“政治”等其他分类中。

如果熵值很低，说明包含这个特征的数据只出现在少数分类中，对于分类的判断有价值。计算出每个特征所对应的数据集之熵，我们就可以按照熵值由低到高对特征进行排序，挑选出排列靠前的特征。

当然，这个做法只考虑了单个特征出现时，对应数据的分类情况，而并没有考虑整个数据集的分类情况。比如，虽然出现“电影”这个词的文章，经常出现在“娱乐”这个分类中，很少出现在其他分类中，但是可能整个样本数据中，“娱乐”这个分类本来就已经占绝大多数，所以“电影”可能并非一个很有信息含量的特征。

为了改进这一点，我们可以借用决策树中信息增益的概念。如果基于某个特征的划分，所产生的信息增益越大，说明这个特征对于分类的判断越有价值。所以，我们可以为计算基于每个特征的划分，所产生的信息增益，然后按照增益值由高到低对特征进行排序，挑选出排列靠前的特征。

利用卡方检验进行特征选择

在统计学中，我们使用卡方检验来检验两个变量是否相互独立。把它运用到特征选择，我们就可以检验特征与分类这两个变量是否独立。如果两者独立，证明特征和分类没有明显的相关性，特征对于分类来说没有提供足够的信息量。反之，如果两者有较强的相关性，那么特征对于分类来说就是有信息量的，是个好的特征。为了检验独立性，卡方检验考虑了四种情况的概率：P(fi,cj)、P(fi¯,cj¯)、P(fi,cj¯)、P(fi¯,cj)。

其中，N 表示数据的总个数。通过这个公式，你可以看到，如果一个特征和分类的相关性很高，无论是正向相关还是负向相关，那么正向相关和负向相关的差值就很大，最终计算的值就很高。最后，我们就可以按照卡方检验的值由高到低对特征进行排序，挑选出排列靠前的特征。

---

29 | 归一化和标准化：各种特征如何综合才是最合理的？

特征变换：

• 归一化
• 标准化

在机器学习领域里，如何使用统计里的数据分布来进行特征值的转换。

• 第一点，为什么有时候需要转换特征值？因为不同类型的特征取值范围不同，分布也不同，相互之间没有可比性。因此在线性回归中，通过这些原始值分析得到的权重，并不能代表每个特征实际的重要性。
• 第二点，如何使用归一化进行特征值转换？这里的归一化是指使用特征取值范围中的最大值和最小值，把原始值转换为 0 到 1 之间的值。这样处理的好处在于简单易行，便于理解。不过，它的缺点也很明显，由于只考虑了最大最小值，因此很容易受到异常数据点的干扰。
• 第三点，如何使用标准化进行转换？经过标准化处理之后，每种特征的取值都会变成一个标准正态分布，以 0 为均值，1 为标准差。和归一化相比，标准化使用了数据是正态分布的假设，不容易受到过大或过小值的干扰。

---

30 | 统计意义（上）：如何通过显著性检验，判断你的A/B测试结果是不是巧合？

A/B 测试

A/B 测试，简单来说，就是为同一个目标制定两个或多个方案，让一部分用户使用 A 方案，另一部分用户使用 B 方案，记录下每个部分用户的使用情况，看哪个方案产生的结果更好。这也意味着，通过 A/B 测试的方式，我们可以拿到使用多个不同方法之后所产生的多组结果，用于对比。

显著性差异

第一，两个分布之间的差异。假设 A 分布的均值小于 B 分布，而两者的方差一致，那么 A 分布随机产生的数据有更高的概率小于 B 分布随机产生的数据。第二，采样引起的差异，也就是说采样数据不能完全体现整体的数据分布。我在之前的图中，用来自 A、B 两组的 10 个数据展示了采样所导致的误差。

如果差异是第一个原因导致的，在统计学中我们就认为这两组“有显著性差异”。如果差异是第二种原因导致的，我们就认为这两组“无显著性差异”。可以看出来，显著性差异（Significant Difference），其实就是研究多组数据之间的差异，是由于不同的数据分布导致的，还是由于采样的误差导致的。通常，我们也把“具有显著性差异”，称为“差异具有统计意义”或者“差异具有显著性”。

这里你还需要注意“差异具有显著性”和“具有显著差异”的区别。如前所说，“差异具有显著性“表示不同的组很可能来自不同的数据分布，也就是说多个组的数据来自同一分布的可能性非常小。而“具有显著差异”，是指差异的幅度很大，比如相差 100 倍。

不过，差异的显著性和显著差异没有必然联系。举两个例子，比如说，两个不同的数据分布，它们的均值分别是 1 和 1.2，这两个均值相差的绝对值很小，也就是没有显著差异，但是由于它们源自不同的数据分布，所以差异是具有显著性的。再比如说，来自同一个数据分布的两个采样，它们的均值分别是 1 和 100，具有显著的差异，但是差异没有显著性。

统计假设检验和显著性检验

统计假设检验是指事先对随机变量的参数或总体分布做出一个假设，然后利用样本信息来判断这个假设是否合理。在统计学上，我们称这种假设为虚无假设（Null Hypothesis），也叫原假设或零假设，通常记作H0。而和虚无假设对立的假设，我们称为对立假设（Alternative Hypothesis），通常记作H1。也就是说，如果证明虚无假设不成立，那么就可以推出对立假设成立。

统计假设检验的具体步骤是，先认为原假设成立，计算其会导致什么结果。若在单次实验中产生了小概率的事件，则拒绝原假设 H0，并接受对立假设 H1。若不会产生小概率的事件，则不能拒绝原假设 H0，从而接受它。因此，统计学中的假设是否成立，并不像逻辑数学中的绝对“真”或“假”，而是需要从概率的角度出发来看。

那么，问题来了，多少才算是“小概率”呢？按照业界的约定俗成，通常我们把概率不超过 0.05 的事件称为“小概率事件”。当然，根据具体的应用，偶尔也会取 0.1 或 0.01 等。在假设检验中，我们把这个概率记为α，并称它为显著性水平。

显著性检验是统计假设检验的一种，顾名思义，它可以帮助我们判断多组数据之间的差异，是采样导致的“偶然”，还是由于不同的数据分布导致的“必然“。当然，这里的“偶然”和“必然”都是相对的，和显著性水平α有关。显著性检验的假设是，多个数据分布之间没有差异。如果样本发生的概率小于显著性水平α，证明小概率事件发生了，所以拒绝原假设，也就是说认为多个分布之间有差异。否则呢，接受原假设，认为多个分布之间没有差异。换句话说，显著性水平α即为拒绝原假设的标准。

P 值

既然已经定义了显著性检验和显著性水平，那么我们如何为多组数据计算它们之间差异的显著性呢？我们可以使用 P 值（P-value）。P 值中的 P 代表 Probability，就是当 H0 假设为真时，样本出现的概率，或者换句话说，其实就是我们所观测到的样本数据符合原假设 H0 的可能性有多大。

如果 P 值很小，说明观测值与假设 H0 的期望值有很大的偏离，H0 发生的概率很小，我们有理由拒绝原假设，并接受对立假设。P 值越小，表明结果越显著，我们越有信心拒绝原假设。反之，说明观测值与假设 H0 的期望值很接近，我们没有理由拒绝 H0。

在显著性检验中，原假设认为多个分组内的数据来自同一个数据分布，如果 P 值足够小，我们就可以拒绝原假设，认为多个分组内的数据来自不同的数据分布，它们之间存在显著性的差异。所以说，只要能计算出 P 值，我们就能把 P 值和显著性水平α进行比较，从而决定是否接受原假设。

---

31 | 统计意义（下）：如何通过显著性检验，判断你的A/B测试结果是不是巧合？

方差分析

方差分析（Analysis of Variance, ANOVA），也叫F 检验。这种方法可以检验两组或者多组样本的均值是否具备显著性差异。它有四个前提假设，分别是：

• 随机性：样本是随机采样的；
• 独立性：来自不同组的样本是相互独立的；
• 正态分布性：组内样本都来自一个正态分布；
• 方差齐性：不同组的方差相等或相近。

SST、SSM 和 SSE

之前我们提到，差异是不是显著性，关键要看这个差异是采样的偶然性引起的，还是分布本身引起的。方差分析的核心思想也是围绕这个展开的，因此它计算了三个数值：SST、SSM 和 SSE。SST 表示所有采样数据的因变量方差（Total Sum of Squares），我把它的计算公式列在这里。

SSM 表示数据分布所引起的方差，我们称它为模型平方和（Sum Of Squares for Model），它的计算公式如下：

SSE 表示采样引起的方差，我们称它为误差平方和（Sum of Squaress for Error）。它的计算公式如下：

SST、SSM 和 SSE 这三者的关系其实是这样的：

你可以把这三者的公式代入，自己证明一下等式是否成立。由此可以看出，SST 是由 SSM 和 SSE 构成的。如果在 SST 中，SSM 的占比更大，那么说明因素对因变量的差异具有显著的影响；如果 SSE 的占比更大，那么说明采样误差对因变量的差异具有更显著的影响。我们使用这两部分的比例来衡量显著性，并把这个比例称为 F 值。具体公式如下：

在这个公式中，s 是水平的个数，n 为所有样本的总数量，s-1 为分布的自由度，n-s 为误差的自由度。你可能对自由度这个概念比较陌生，这里我稍微解释一下。

自由度

自由度（degree of freedom），英文缩写是 df，它是指采样中能够自由变化的数据个数。对于一组包含 n 个数据的采样来说，如果方差是一个固定值，那么只有 n-1 个数据可以自由变化，最后一个数的取值是给定的方差和其他 n-1 个数据决定的，而不由它自己随意变化，所以自由度就是 n-1。这也是为什么在计算一组数的方差时，我们在下面这个公式中使用的除数是 n-1，而不是 n。

使用 Python 代码进行验证

安装 Python 的扩展包 statsmodels。

pip install -U statsmodels

---

32 | 概率统计篇答疑和总结：为什么会有欠拟合和过拟合？

拟合、欠拟合和过拟合

• 适度拟合（right fitting）
• 欠拟合（Under Fitting）
• 过拟合（Over Fitting）

如何处理欠拟合和过拟合？

欠拟合问题，产生的主要原因是特征维度过少，拟合的模型不够复杂，无法满足训练样本，最终导致误差较大。因此，我们就可以增加特征维度，让输入的训练样本具有更强的表达能力。

过拟合问题产生的主要原因则是特征维度过多，导致拟合的模型过于完美地符合训练样本，但是无法适应测试样本或者说新的数据。所以我们可以减少特征的维度。之前在介绍决策树的时候，我提到了这类算法比较容易过拟合，可以使用剪枝和随机森林来缓解这个问题。

剪枝，顾名思义，就是删掉决策树中一些不是很重要的结点及对应的边，这其实就是在减少特征对模型的影响。虽然去掉一些结点和边之后，决策树对训练样本的区分能力变弱，但是可以更好地应对新数据的变化，具有更好的泛化能力。至于去掉哪些结点和边，我们可以使用前面介绍的特征选择方法来进行。

随机森林的构建过程更为复杂一些。“森林”表示有很多决策树，可是训练样本就一套，那这些树都是怎么来的呢？随机森林算法采用了统计里常用的可重复采样法，每次从全部 n 个样本中取出 m 个（m

从另一个角度来看，过拟合表示模型太复杂，而相对的训练数据量太少。因此我们也可以增加训练样本的数据量，并尽量保持训练数据和测试数据分布的一致性。如果我们手头上有大量的训练数据，则可以使用交叉验证（Cross Validation）的划分方式来保持训练数据和测试数据的一致性。其核心思想是在每一轮中，拿出大部分数据实例进行建模，然后用建立的模型对留下的小部分实例进行预测，最终对本次预测结果进行评估。这个过程反复进行若干轮，直到所有的标注样本都被预测了一次而且仅一次。如果模型所接受的数据总是在变化，那么我们就需要定期更新训练样本，重新拟合模型。

总结

第二模块中，我介绍了很多概率统计中常用的概念。随机变量和它的概率分布体现了事物发生的不确定性。而条件概率、联合概率和边缘概率体现了多个随机变量之间的关系以及是不是相互独立，通过这三者的关系，我们可以推导出贝叶斯定理。在贝叶斯定理和变量独立性假设的基础之上，我讲了朴素贝叶斯算法中的公式推导，以及如何使用先验概率来预测后验概率。由于朴素贝叶斯假定多个变量之间相互独立，因此特别适合特征维度很多、特征向量和矩阵很稀疏的场景。基于词包方法的文本分类就是个非常典型的例子。

文本分类涉及了词与词之间相互独立的假设，然后延伸出多元文法，而多元文法也广泛应用在概率语言模型中。语言模型是马尔科夫模型的一种，而隐马尔科夫模型在马尔科夫模型的基础之上，提出了两层的结构，解决了我们无法直接观测到转移状态的问题。

由概率知识派生而来的信息论，也能帮助我们设计机器学习的算法，比如决策树和特征选择。统计中的数据分布可以让特征值转换更合理，而假设检验可以告诉我们哪些结论是更可靠的。

由于很多监督式学习都是基于概率统计的，所以我使用了一些学习算法来进行讲解。你会发现，概率和统计可以帮助这些算法学习训练样本中的特征，并可以对新的数据进行预测，这就是模型拟合的过程。