模糊逻辑(Fuzzy Logic)
参考:https://blog.csdn.net/weixin_34248118/article/details/87420025
要想了解模糊逻辑,首先我们要知道对应的另外一种逻辑,布尔逻辑。
1. 经典的布尔逻辑
布尔数值就是0和1,是和非,也是计算机逻辑的基础,其基本运算就是"与、或、非",体现在编程中就是“If .... then...”。
布尔逻辑赋予计算机自动判断和决策的能力,但是却并不完美,甚至限制了计算机的能力,因为人类判断和决策往往没那么简单。比如布尔逻辑能够很好处理那种是非很清晰的场景,比如用电脑可以轻松编写“如果下雨就提醒我出门带伞“”这样的程序,因为下不下雨是一个清晰的是非逻辑。
然而人在实际决定带不带伞出门时常是考虑雨的大小,雨会下多久。那多大的雨算大雨需要带伞,多小的雨算小雨不用带伞呢?这里并没有一个清晰的雨量门槛决定人是否带伞。
模糊逻辑就是用来解决这样的分类和决策难题的。
2. 隶属度(Degree of Membership)
在模糊逻辑的眼中,大雨,小雨,和中雨之间是没有严格的界限的,也就是说某一种雨量的大小并不完全归属于某一个类,而是以隶属度来衡量的。比如对于10mm降雨,隶属于小雨的隶属度为0.5, 中雨的隶属度为0.4,大雨的隶属度为0.1;对于100mm降雨,小雨的隶属度为0, 中雨的隶属度为0.3,大雨的隶属度为0.7。
将逻辑的输入数值(降雨量)转化成各个集合(小雨,中雨,大雨)的隶属度的过程就叫做Fuzzification。 也是模糊逻辑的第一步。
3. Fuzzyfication(模糊化)
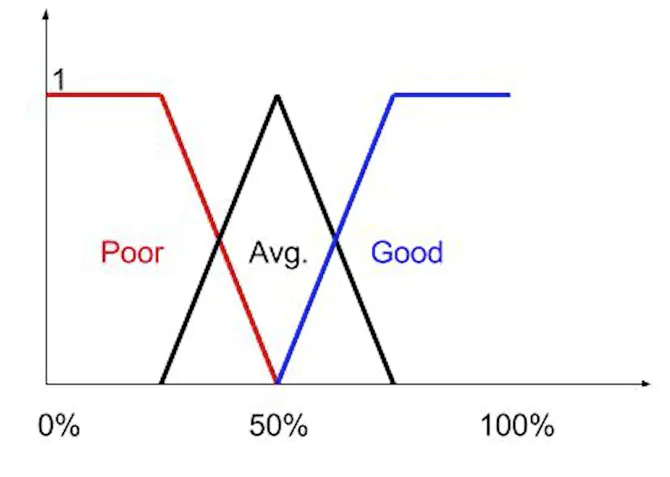
如何确定输入数值与隶属度的关系呢,这就要用到隶属度函数,隶属度函数的图形可以是任意的,但常用的方法是三角形或者梯形。 例如下图的形式。
上图是考试分数和学生成绩的隶属度关系。 比如考0分,Poor的隶属度为1,Avg. 和Good为0。 考试为32.5分(红黑交叉点),Poor的隶属度为0.5,Avg.为0.5, Good为0。 在任意一点都能找到其所对应的集合的隶属度。
隶属度函数的确立目前还没有一套成熟有效的方法,大多数系统的确立方法还停留在经验和实验的基础上。对于同一个模糊概念,不同的人会建立不完全相同的隶属度函数,尽管形式不完全相同,只要能反映同一模糊概念,在解决和处理实际模糊信息的问题中仍然殊途同归。
下面是几种常用的方法。(1)模糊统计法;(2)例证法;(3)专家经验法;(4)二元对比排序法
4. 模糊逻辑的“与,或,非”运算
模糊逻辑的运算实际上就是模糊逻辑中分解出的各个隶属度的运算。我们将逻辑的两个输入定义为A,B,输出为C(A与B -> C),举个例子,A = Poor: 0.5(Poor的隶属为0.5 )B = Good:0.2, 那么C= A与B是多少呢?
其实有好多计算C的方法,这里介绍一个最简单的“最小隶属法(MIN implication)”,于是 C=A与B中最小那个(0.2)。于是C= Good: 0.2.
那D = A或B怎么计算呢?还是介绍一个最简单的“最大隶属法(MAX implication)”,即 C=A或B中最大的那个(0.5)。 于是D= Poor: 0.5
"非"的运算就更简单了,直接如下图所示取相反的折线就完了。
5. 模糊逻辑的决策规则(Rule Base)
将输入模糊化了之后,需要通过规则,和模糊逻辑的运算来重新组合。下面我们通过一个实例来介绍一下什么是模糊逻辑的规则。
你要编写一个程序来给自己分配食物,食物的多少由你饥饿的程度(Hunger)和食物的味道(Taste)共同决定的,两者分别有少、中、多(S, M, L)三个集合
如下图,表格为规则,例如:Taste(M)与Hunger(M)输出M,Hunger(M)与Taste(L)输出L;隶属度函数在表格下面。以Taste 和 Hunger分别取值为5.625和5为例,参考给定的隶属度函数,模糊化之后 Taste(S)=0,Taste(M)=0.75,Taste(L)=0.25, Hunger(S)=0, Hunger(M)=1, Hunger(L)=0。
可见除了规则表中标记成红色和绿色的部分,其他的输出都为0。
表中:
- 红色M是Taste(M)与Hunger(M)的输出结果可以用最小法则Min(0.75, 1)=0.75
- 绿色L是Taste(L)与Hunger(M)的输出结果可以用最小法则Min(0.25, 1)=0.25
注:红色部分跟原文不同,是根据本人理解进行的更正。如有异议,可留言讨论
同样的如果Taste和Hunger分别取5.625和4.375,会有如下图结果:
表中:
- 红色S是Taste(M)与Hunger(S)的输出结果可以用最小法则Min(0.75, 0.25)=0.25
- 绿色M是Taste(M)与Hunger(M)的输出结果可以用最小法则Min(0.75, 0.75)=0.75
- 黄色M是Taste(L)与Hunger(S)的输出结果可以用最小法则Min(0.25, 0.25)=0.25
- 紫色L是Taste(L)与Hunger(M)的输出结果可以用最小法则Min(0.25, 0.75)=0.25
- 其他输出为0。
这些输出我们在模糊逻辑中定义为Fire Strength(FS)。
6. 去模糊化(De-fuzzyfication)
模糊逻辑通过模糊化将输入的数值转化成各个集合的隶属度之后,再通过规则和运算得到若干个FS。这些FS并不能为我们解决实际问题。以之前分配食物为例,我们期望的是:给出任意两个输入值(Taste 和 Hunger)能输出一个确定的数值,这时我们就要用去模糊化来得到这个输出值了。
去模糊化有很多方法,这里我同样只介绍一个简单和应用广泛的方法:加权平均判决法

其中FS就是上一步输出的Fire Strength, OW (Output Wight)是权重。权重通常是取每个集合的中间值,分配食物的例子OW(S)=2.5, OW(M)=5, OW(L)=7.5。
如果Taste = 5.625, Hunger = 4.375
FS1(S)=0.25, FS2(M)=0.75, FS3(M)=0.25, FS4(L)=0.25.
用上面的公式可以求得
Output = (0.252.5+0.755+0.255+0.257.5)/(0.25+0.75+0.25+0.25)=5
这个输出有什么用呢?你可以通过这个输出决定是否分配食物,设定一个阈值,比如为4,如果小于等于这个阈值就不分配食物,大于这个阈值就分配食物。这里输出是5,那么就可以给自己分配食物了。还可以通过设置多个阈值,来决定分配给自己食物的多少。
另外去模糊化方法:最大值均值法;中心法;最大值平均法等。
模糊计算的应用:推荐系统;控制领域的专家系统
演化:模糊神经网络系统
汇集神经网络和模糊计算是优点,即人工神经网络具有 较强的自学习和联想功能能力,人工干预少,精度较高,对专家知识的利用也较好;而模糊计算的特点有 推理过程容易理解、专家知识利用较好、对样本的要求较低等。
1. 利用神经网络,来学习、演化模糊规则库。类似数据挖掘的过程,模糊竞争学习算法 : 利用神经网络来增强的 模糊计算系统
2. 利用模糊控制方法,不断改善神经网络的性能,如模糊BP算法 :利用模糊计算增强的神经网络