GCNS论文总结

GCNS论文总结

主要内容：

一、GCN背景发展
二、Laplacian 矩阵
三、图傅里叶变换
四、GCN卷积实现
五、GCN任务分类/应用
六、谈谈感受

一、GCN背景发展
CNN在图像处理任务中应用广泛，但不能处理graph data(the local translational invariance)。近年来，graph data学习需求日益凸显，谱图、统计分析等Graph Learning理论相继涌现。
随着深度学习的兴起，深度学习模型被引入graph data中，代表性工作是Network Embedding（如DeepWalk、LINE、node2vec），其建模为两阶段问题：（节点分类）为每个节点学习统一长度的表达，节点表达作为输入，训练分类模型。
同时，人们开始用深度学习对图数据进行端到端的建模，GCN则是其中最活跃的一支。
思考1：为什么引入GCN?

二、Laplacian 矩阵
2.1 定义和分类
Graph Fourier Transformation及GCN定义都用到图的Laplacian 矩阵。
G=(V,E)的Laplacian 矩阵定义：L=D−A。

三种常用的Laplacian：

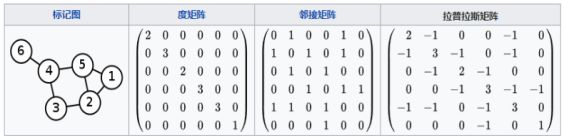
思考：GCN为什么要用Laplacian矩阵？
2.2 Laplacian谱分解（特征分解，对角化）
实对称半正定矩阵。GCN的核心基于Laplacian矩阵谱分解。
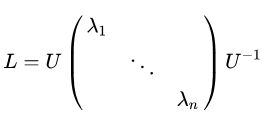或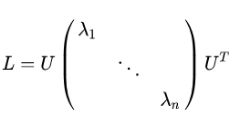
上述两者等价。

思考3：什么是半正定矩阵？它的性质有哪些？
思考4：Laplacian矩阵为什么能谱分解？

三、图傅里叶变换(Graph Fourier Transform, GFT)
3.1卷积定理
函数卷积的傅立叶变换是函数傅立叶变换的乘积。

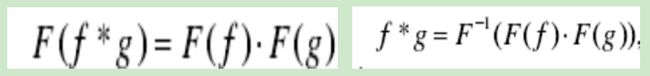
3.2 传统FT、卷积推广到GFT及卷积
即把Laplacian算子的特征函数变为Graph对应的拉普拉斯矩阵的特征向量。
3.2.1 传统的傅里叶变换：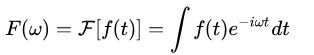
3.2.2 GFT定义
图信号由spatial domain视角转化到频域frequency domain视角。

根据卷积定理得，f与卷积核h在Graph上的卷积：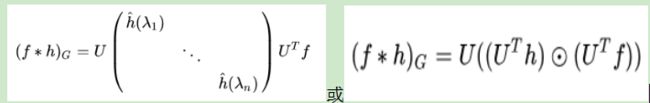
思考5：spatial domain和frequency domain是什么？
思考6：为什么要在频率域中进行图像处理？
思考7：为什么Laplacian矩阵的特征向量可为GFT基？

四、GCN卷积实现
GCN主要包括卷积算子和池化算子的构建。其中，卷积算子包括谱方法和空间方法。
4.1 GCN谱方法
谱方法：用图上卷积定理从谱域定义图卷积。
用卷积定理，对谱空间信号做乘法，再利用傅里叶逆变换将信号转换到原空间来实现图卷积，避免图数据不满足平移不变性而造成的卷积定义困难问题。

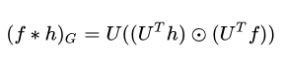
4.1.1 代表GCNs 举例：
CNN共享参数的 kernel系数由随机化初值确定，根据误差函数通过反向传播梯度下降进行迭代优化。


θ1,θ2,…,θn是任意的参数，
创新：将CNN泛化到非欧几里得空间,首次引入Spectral-based GCN
优势：大大减少神经网络中的参数数量，而不会使测试误差恶化（并且经常改善），并使正向传播更快，可以扩展到具有具有局部性概念的大量坐标的数据
不足：
①计算代价较高，O(n2)；
②卷积核无spatial localization
③卷积核参数多。
（2）Convolutional neural networks on graphs with fast localized spectral filtering. NIPS 2016. ChebyNet（Text Categorization on 20NEWS，MNIST，FC,softmax regression，）

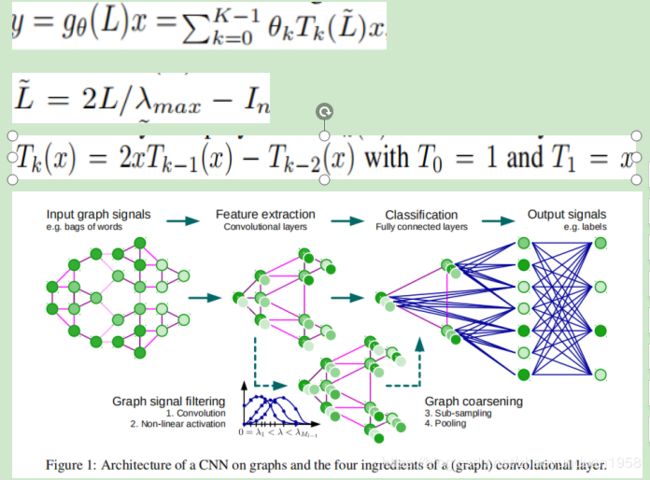
创新：所定义的卷积公式严格局部定位
粗化图（借助顶点、顶点之间的关系-边等将图简化），代替池化。
思考8：ChebyNet 优点是什么？

（3）Semi-Supervised Classification with Graph Convolutional Networks. ICLR 2017（a two-layer GCN，）为进一步简化计算，采用1阶Chebyshev多项式并限制λmax≈2,

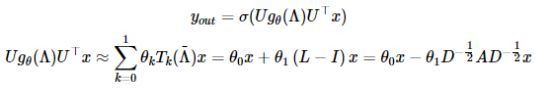
创新：使用1阶Chebyshev多项式
（4）其他改进。如H-GCN（思考：4个通道怎么实现？精化层怎么实现？）
（5）Bingbing Xu, Huawei Shen, Qi Cao, Yunqi Qiu, and Xueqi Cheng. Graph wavelet neural network// Proceedings of the International Conference on Learning Representations. New Orleans, USA, 2019（小波神经网络GWNN）。提出用小波变换代替傅立叶变换实现卷积定理。和傅立叶变换相比，小波变换的基底具有几个很好的性质：小波变换的基底可以通过切比雪夫多项式近似得到，避免拉普拉斯矩阵特征分解的高昂代价；小波变换的基底具有局部性;小波基底的局部性使得小波变换矩阵非常稀疏，大大降低计算复杂度。
另外，图热核网络(GraphHeat)从滤波器的角度对上谱方法进行分析，指出谱卷积神经网络是非参滤波器，而切比雪夫网络和一阶图卷积神经网络都是高通滤波器，但这与图半监督学习的任务中平滑性先验不一致，基于此，图热核网络利用热核函数参数化卷积核，进而实现低通滤波器。

4.2 GCN空间方法
从节点域出发，通过定义聚合函数来聚合每个中心节点和其邻近节点。
ChebyNet和一阶GCN以Laplacian矩阵或其变体作为聚合函数。在此启发下，近期有人通过注意力机制或递归神经网络等直接从节点域学习聚合函数，此外，也有一些工作从空间角度定义了图卷积神经网络的通用框架并解释图卷积神经网络的内部机制。
比如，Learning convolutional neural networks for graphs. ICML 2016，提出算法PATCHY-SAN(Select Assemble Normalize)，即先将图结构数据CNN可处理的序列结构（欧式数据格式），再做卷积。具体步骤：
（1）Node Sequence Selection
用 labeling算法（between centrality， Weisfeiler-Lehman algorithm）将图节点集合根据向心性（节点的度、中心度等）映射为有序的节点序列。从中以间隔s隔段选取w个节点构成最终的节点序列。
（2）Neighborhood Assembly
对节点序列中的每个节点，利用BFS扩展邻居节点，和源节点一起构成一个至少k大小的邻域集合.
（3）Graph Normalization
对由当前节点及其对应的邻居构成的子图进行规范化，作为卷积结构的输入。（使用NAUTY算法, 对邻域集合排序, 排序截取前k个，得到感受野受域）

通过上述三个步骤构建出所有的卷积片之后，利用卷积结构分别对每个分片进行操作。

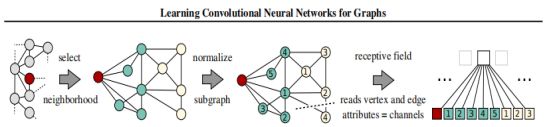
主要缺点：
①每个顶点提取出来的neighbors不同，使得计算处理必须针对每个顶点
②提取特征的效果可能没有卷积好。

五、GCN任务分类/应用

5.1 Node Level任务
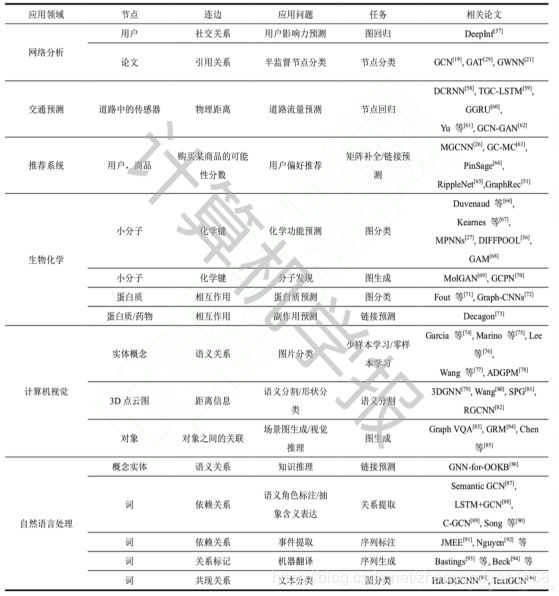
主要有分类任务和回归任务。节点任务：引文网络中的文章分类，社交网络用户标签分类、恶意账户检测等。
论文：GCN、GAT GWNN（节点分类）
DGCRNN、TGC-LSTM（节点回归）
5.2 Link Level任务
主要有边分类和预测任务。边分类：对边的某种性质进行预测；边预测是指给定的两个节点之间是否会构成边。应用场景比如在社交网络中，将用户作为节点，用户之间的关注关系建模为边，通过边预测实现社交用户的推荐。目前，边层面的任务主要集中在推荐业务中。
论文：MGCNN（链接预测）
5.3 Graph Level任务
从图整体结构出发，实现分类、表示和生成等任务。目前，图层面的任务主要应用在自然科学研究领域，比如蛋白质网络中的蛋白质分类、药物网络生成等。
论文：MPNNS（生 图分类）Graph-VQA(CV 图生成)

六、谈谈感受
6.1 博采众长，创造模型 H-GCN
6.2 他山之石，为我所用 DeepWalk.
6.3 用其他变换代替GFT，或多种变换结合，构建卷积核