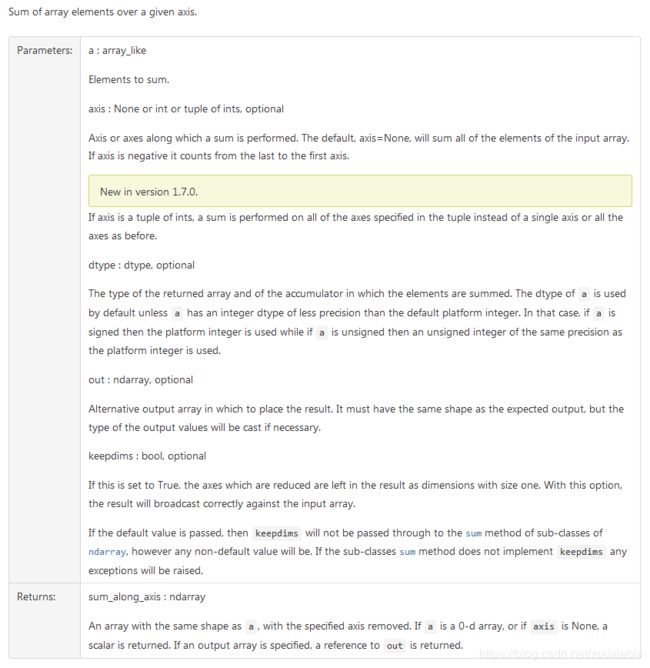
numpy.sum维度的思考

一个简单的例子

首先看个你觉得很简单的例子

>>> print(sum(range(5),-1))
>>> from numpy import *
>>> print(sum(range(5),-1))
9
10

两行打印分别是9和10，是不是有些奇怪？首先来看第一行打印：
print(sum(range(5),-1))

这里调用的是python原生的sum接口：
sum(iterable[, start])

python的解释如下：

Sums start and the items of an iterable from left to right and returns the total. start defaults to 0. The iterable’s items are normally numbers, and the start value is not allowed to be a string.

python原生的sum()指定可迭代对象进行求和，start指定相加的参数，如果没有设置这个值，默认为0。已经说的很清楚了，再来看几个例子。

>>> sum([0,1,2])
3
>>> sum((2, 3, 4), 1)        # 元组计算总和后再加 1
10
>>> sum([0,1,2,3,4], 2)      # 列表计算总和后再加 2
12

因此第一个打印中的求和是 0，1，2，3，4，-1 这六个数字求和，结果是9。

第二行，因为导入了numpy包，再调用sum()就会被numpy中sum()覆盖，因此第三行中的sum()，调用的已不是python原生的sum()接口了，而是numpy.sum()。

那么我们来看看numpy.sum()有什么特殊之处吧。

numpy.sum(a,
          axis=None,
          dtype=None,
          out=None,
          keepdims=)

numpy中的sum()有5个参数，其中第二个参数表示维度，也就是 a 求和的方向。在我们的例子中：
print(sum(range(5),-1))

第二个参数是 -1， 是不是用错了呢？有 -1 维吗？其实在这里 -1 表示最后一个维度，因为我们的数组是一维的，所以它就表示第一个维度，也即最后一个维度，那么就是在第一个维度上求和。第一个维度上的元素：0，1，2，3，4，求和之后得出 10，这也就是第二个打印为什么是 10 得原因了。

拓展

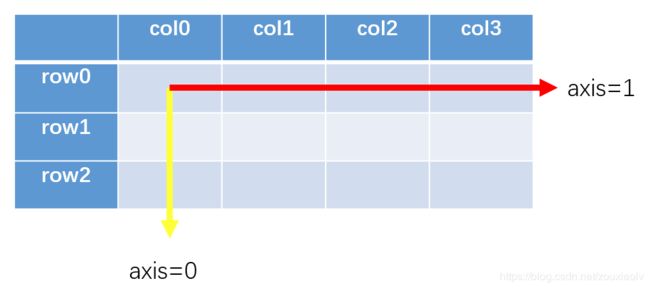
对于多维数组，怎么根据维度求和呢？

上图是个 3*4 的numpy.array，根据 ndims ，存在两个维度，第一维度和第二维度，axis=0 代表在第一维度求和，可以理解为将行压缩；axis=1，代表在第二个维度上求和，可以理解为将列压缩。看例子：

>>> array = np.random.random((3, 4))
>>> print(np.sum(array, axis=0, keepdims=True))
>>> print('---------------------------------------------')
>>> print(np.sum(array, axis=1, keepdims=True))
[[2.01429427 1.52364443 1.18641048 1.00423807]]
---------------------------------------------
[[2.56295628]
 [1.42019516]
 [1.7454358 ]]

 再看一个三维的例子：

>>> c = np.array([[[0, 1, 2, 3],
                   [4, 5, 6, 7]],
                  [[1, 2, 3, 4],
                   [5, 6, 7, 8]]])
>>> print(np.sum(c, axis=0))
>>> print('-----------------')
>>> print(np.sum(c, axis=1))
>>> print('-----------------')
>>> print(np.sum(c, axis=2))
[[ 1  3  5  7]
 [ 9 11 13 15]]
-----------------
[[ 4  6  8 10]
 [ 6  8 10 12]]
-----------------
[[ 6 22]
 [10 26]]

怎么理解 axis 等于不同值时的求和？我们可以看到这是一个三维数组，它的形状是 2*2*4。

>>> print(c.shape)
(2, 2, 4)
>>> print(c.ndim)
3

可以这么理解，首先可以把 c 可以看作一个 2*2 的矩阵，而矩阵的每个元素是一个长度为4的数组，例如 [0, 1, 2, 3]，因此 c 是一个三维array。当参数 axis=0 时，求矩阵每一列上元素的和。例如，对第一列上的两个数组 [0, 1, 2, 3] 和 [1, 2, 3, 4] 相加，返回一个新的数组 [1, 3, 4, 7]，后面的列依次类推。因此最后得到一个新的数组，即：

>>> np.sum(c, axis = 0)
array([[ 1,  3,  5,  7],
       [ 9, 11, 13, 15]])

axis=1 时，对矩阵每一行上的元素进行求和，同上。

axis=2时，对矩阵每个元素进行求和，即对矩阵中每个列表内的元素求和，返回一个新的 2*2 矩阵。这听起来有些奇怪，但前提必须是一个三维数组，且 axis 的值必须小于数组的维度，因为只能在数组存在的维度上求和，否则会出现异常。

另外一种比较通用的理解：你的输入矩阵的 shape 是 (2,2,4)，那么当 axis=0 时，就是在第一个 dimension 上进行求和，最后得到的结果的 shape 就是去掉第一个 dimension 后的 shape，也就是 (2,4)。具体的计算方法则是，对于,假设输出矩阵为，第一个 dimension 求和:

                                                                  

如果 axis=1，那么输出 shape 就是去掉第二个 dim，也就是(2,4)，计算是：

                                                                 

如果 axis=2，那么输出 shape 就是去掉第三个 dim，也就是(2,2)，计算是:

                                                                  

对于高维数据求和，一般按 axis 对应的维度求和，其他维度的位置和形状不变，最后的 shape 为去掉对应维度的形状。