LeetCode 115. 不同的子序列（DP）

1. 题目

给定一个字符串 S 和一个字符串 T，计算在 S 的子序列中 T 出现的个数。

一个字符串的一个子序列是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，“ACE” 是 “ABCDE” 的一个子序列，而 “AEC” 不是）

题目数据保证答案符合 32 位带符号整数范围。

示例 1：
输入：S = "rabbbit", T = "rabbit"
输出：3
解释：
如下图所示, 有 3 种可以从 S 中得到 "rabbit" 的方案。
(上箭头符号 ^ 表示选取的字母)

rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

示例 2：
输入：S = "babgbag", T = "bag"
输出：5
解释：
如下图所示, 有 5 种可以从 S 中得到 "bag" 的方案。 
(上箭头符号 ^ 表示选取的字母)

babgbag
^^ ^
babgbag
^^    ^
babgbag
^    ^^
babgbag
  ^  ^^
babgbag
    ^^^

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/distinct-subsequences
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

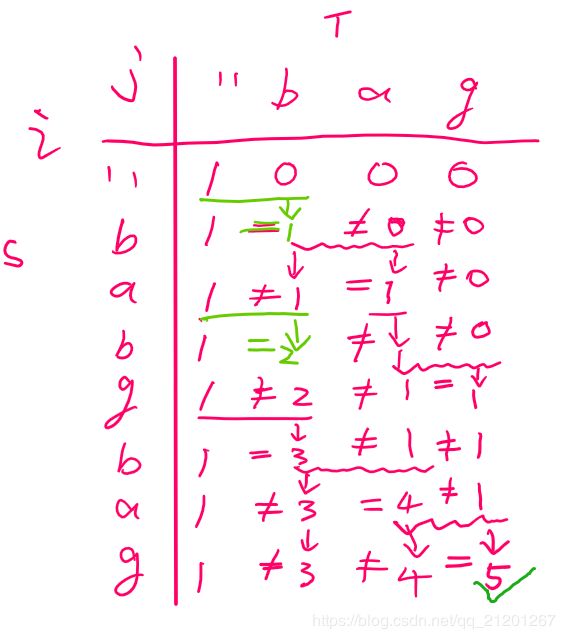
• dp[i][j] 表示 在S的前 i 个字符中，能找到T的前 j 个字符

class Solution {
public:
    int numDistinct(string s, string t) {
        if(t=="") return 1;
        if(s.size() < t.size()) return 0;
        int m = s.size(), n = t.size(), i, j;
        vector<vector<long>> dp(m+1, vector<long>(n+1,0));
        for(i = 0; i <= m; ++i)
            dp[i][0] = 1;
        for(j = 1; j <= n; j++)//T字符
        {
        	for(i = 1; i <= m; i++)//S字符
        	{
        		if(s[i-1]==t[j-1])//相等时，相比下面不相等时，多了一种情况
        		//让 i, j, 匹配，前面的有多少种情况，dp[i-1][j-1]
        			dp[i][j] = dp[i-1][j-1]+dp[i-1][j];
        		else//不相等时，相当于第i个字符没有用
        			dp[i][j] = dp[i-1][j];
        	}
        }
        return dp[m][n];
    }
};

20 ms 13.4 MB

注意：空字符能从任意字符串中找到

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！