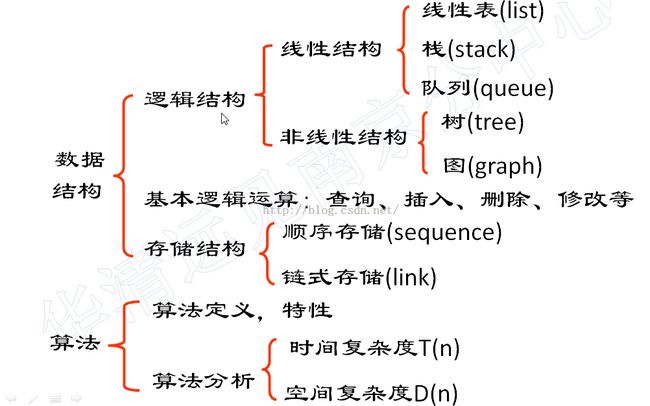
Linux C 数据结构——队列
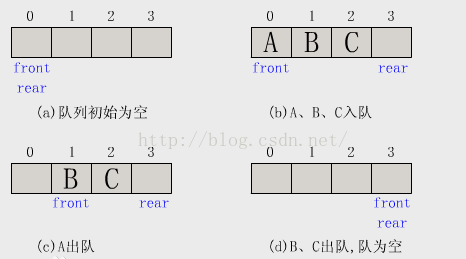
还是先放这张图,以便对比和理解:
队列是限制在两端进行插入操作和删除操作的线性表,允许进行存入操作的一端称为“队尾”,允许进行删除操作的一端称为“队头”。当线性表中没有元素时,称为“空队”。特点:先进先出(FIFO)。
每次在队尾插入一个元素是,rear增1;每次哎队头删除一个元素时,front增1。随着插入和删除操作的进行,队列元素的个数不断变化,队列所占的存储空间也在为队列结构所分配的连续空间中移动。当front=rear时,队列中没有任何元素,称为空队列。当rear增加到指向分配的连续空间之外时,队列无法再插入新元素,但这时往往还有大量可用空间未被占用,这些空间是已经出队的队列元素曾经占用过得存储单元。
在实际使用队列时,为了使队列空间能重复使用,往往对队列的使用方法稍加改进:无论插入或删除,一旦rear指针增1或front指针增1 时超出了所分配的队列空间,就让它指向这片连续空间的起始位置。自己真从N(MaxSize)增1变到0,可用取余运算rear%N和front%N来实现。这实际上是把队列空间想象成一个环形空间,环形空间中的存储单元循环使用,用这种方法管理的队列也就称为循环队列。
在循环队列中,当队列为空时,有front=rear,而当所有队列空间全占满时,也有front=rear。为了区别这两种情况,规定循环队列最多只能有MaxSize-1个队列元素,当循环队列中只剩下一个空存储单元时,队列就已经满了。因此,队列判空的条件时front=rear,而队列判满的条件时front=(rear+1)%MaxSize。
总结:
1、队头指针front,指向队头元素的位置的前一个位置。即指向预留的位置;
2、队尾指针rear,指向队尾元素的位置;
3、入队: rear = (rear + 1) % N (maxsize),然后元素放入队尾rear所指向的位置;
4、出队: front = (front + 1) % N,然后取出队头指针front所指向的元素;
5、队空: front == rear;
6、队满: (rear + 1) % N == front, N为数组的元素个数;
7、为了区别空队和满队,满队元素个数比数组元素个数少一个。
下面是顺序队列的运算:
顺序队列也是顺序表的一种,具有顺序表同样的存储结构,由数组定义,配合使用数组下表表示的队头指针和队尾完成各种操作:
#define N 64 //队列中数据元素的数据类型
typedef int data_t;
typedef struct
{
data_t data[N]; //用数组作为队列的储存空间
int front,rear; //指示队头位置和队尾位置的指针
}sequeue_t;
1、创建空队列
sequeue_t *CreateEmptySequeue()
{
sequeue_t *queue;
queue = (sequeue_t *)malloc(sizeof(sequeue_t));
if (NULL == queue) return NULL;
queue->front = queue->rear = 0;
return queue;
}2、摧毁一个队列
void DestroySequeue(sequeue_t *queue)
{
if (NULL != queue)
{
free(queue);
}
}3、判断一个队列是否为空
int EmptySequeue(sequeue_t *queue)
{
if (NULL == queue)
return -1;
return (queue->front == queue->rear ? 1 : 0);
}4、判断一个队列是否为满
int FullSequeue(sequeue_t *queue)
{
if (NULL == queue) return -1;
return ((queue->rear + 1) % N == queue->front ? 1 : 0);
}5、清空一个队列
void ClearSequeue(sequeue_t *queue)
{
if (NULL == queue) return;
queue->front = queue->rear = 0;
return;
}6、入队
int EnQueue(sequeue_t *queue, data_t x)
{
if (NULL == queue) return - 1;
if (1 == FullSequeue(queue)) return -1; /* full */
queue->rear = (queue->rear + 1) % N;
queue->data[queue->rear] = x;
return 0;
}7、出队
int DeQueue(sequeue_t *queue, data_t *x)
{
if (NULL == queue) return -1;
if (1 == EmptySequeue(queue)) return -1; /* empty */
queue->front = (queue->front + 1) % N;
if (NULL != x) {
*x = queue->data[queue->front];
}
return 0;
}
二、链式队列
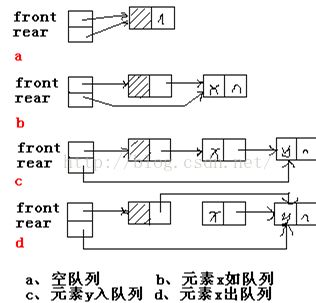
用链表表示的队列简称为链队列,如下图所示
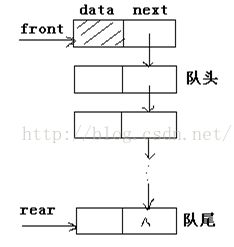
一个链队列显然需要两个分别指示队头和队尾的指针(分别成为头指针和尾指针)才能唯一确定。这里,和线性表的单链表一样,为了操作方便起见,我们也给队列添加一个头结点,并令头指针指向头节点。由此,空的链队列的判决条件为头指针和尾指针均指向头结点,如下图所示:
链队列的操作记为单链表的插入和删除操作的特殊情况,插入操作在队尾进行,删除操作在队头进行,由队头指针和队尾指针控制队列的操作:
typedef int data_t;
typedef struct node_t
{
data_t data;
struct node_t *next;
}linknode_t,*linklist_t;
typedef struct
{
linklist_t front,rear;
}linkqueue_t;1、创建空队列
linkqueue_t *CreateEmptyLinkqueue()
{
linkqueue_t *lp = (linkqueue_t *)malloc(sizeof(linkqueue_t));
if(lp == NULL)
return;
lp->front = lp->rear = (linknode_t *)malloc(sizeof(linknode_t));
if(lp->front == NULL)
return;
lp->front->next = NULL;
return lp;
}
2、摧毁一个链队列
void DestroyLinkqueue(linkqueue_t *queue)
{
if(queue != NULL)
{
ClearLinkqueue(queue);
free(queue);
}
}3、清空一个链队列
void ClearLinkqueue(linkqueue_t *queue)
{
linknode_t *qnode;
while(q->front)
{
qnode = queue->front;
queue->front= qnode->next;
free(qnode);
}
queue->rear = NULL;}4、判断链队列为空
int EmptyLinkqueue(linkqueue_t *queue)
{
if(queue == NULL)
return -1;
return(queue->front == queue->rear ? 1 : 0);
}5、入队
int EnQueue(linkqueue_t *queue,data_t x)
{
linknode_t *node_new;
if(queue == NULL)
return -1;
node_new = (linknode_t *)malloc(sizeof(linknode_t));
if(node_new == NULL)
return -1;
node_new->data = x;
node_new->next = NULL;
if(queue->front->next == NULL)
{
queue->front->next = queue->rear = node_new;
}
else
{
queue->rear->next = node_new;
queue->rear = node_new;
}
return 0;
}6、出队
int DeQueue(linkqueue_t *queue,data_t *x)
{
linknode_t *node_remove;
if(queue == NULL || queue->front->next == NULL)
return -1;
node_remove = queue->front->next;
queue->front->next = node_remove->next;
if(x != NULL)
*x = node_remove->data;
free(node_remove);
return 0;
}