Pytorch：Zero to GANs第二部分：线性回归和梯度下降

翻译自：/jovian

本文目标：创建一个模型，通过平均温度，降雨量，湿度来预测苹果和橙子的产量。
在线性回归的模型中， 每个目标变量被一串权重（weight）和其他变量的乘积和偏差（bias）的求和表示，如：

yield_apple  = w11 * temp + w12 * rainfall + w13 * humidity + b1
yield_orange = w21 * temp + w22 * rainfall + w23 * humidity + b2 

系统设置

import numpy as np
import torch

处理训练数据

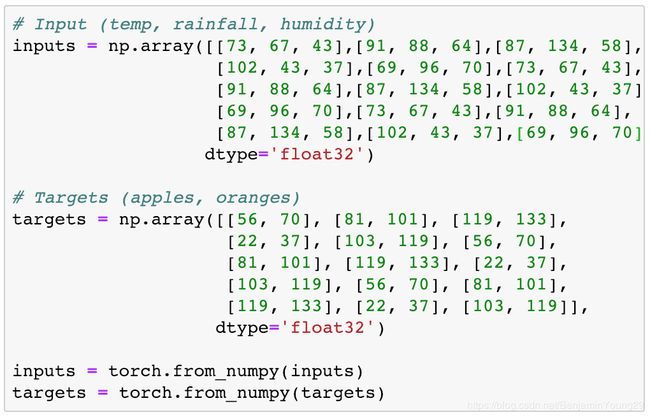
训练数据放在两个矩阵中。分别是ipnuts和targets。每行表示一组观测数据。

#input(temp,rainfall, humidity)
inputs=np.array([[73,67,43],
							[91,88,64],
							[87,134,58],
							[102,43,37],
							[69,96,70]], dtype='float32')
#targets(apples, oranges)
targets=np.array([[56,70],
							[81,101],
							[119,133],
							[22,37],
							[103,119], dtype='float32')

将input和target分开处理。同时类型为numpy。因为这就是通常对待training data的方法：读取csv文件作为numpy arrays，做一些处理，然后转换成PyTorch的张量如下：

#Convert input and targets to tensors
inputs=torch.from_numpy(inputs)
targets=torch.from_numpy(targets)
print(inputs)
print(targets)

线性回归模型

权重和偏差都可以表现成矩阵。这样方便利用GPU进行矩阵运算。随机初始化值，不需要特定。w是23的矩阵，第一行是apple的weight。b同理，是21的矩阵。

# Weight and bias
w=torch.randn(2,3,requires_grad=True)
b=torch.randn(2, requires_grad=True)
print(w)
print(b)

torch.randn返回一个给定形状的张量，值是从正态分布中随机挑选出来的。平均值为0，标准差为1.
线性回归就是普通的执行矩阵运算。将x*wT+b

def model(x):
	return x @ w.t() + b # PyTorch 中@表示矩阵乘法， .t表示返回张量的转置

model返回了预测的数据。


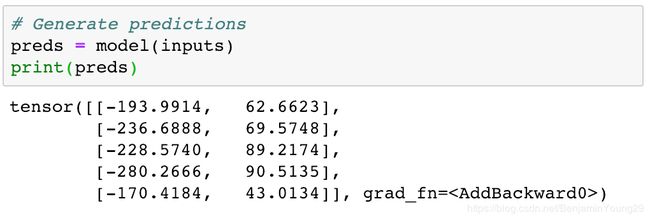
可以看出差距非常大。预测不准确。不过这是因为我们的初始化的权重跟偏差是随机的。所以接下来需要进行修正。

Loss Function

提升模型之前我们需要一个方法来衡量模型表现怎样。我们可以通过算loss 来对比预测值与实际值。方法如下：

• 计算两个矩阵pred和targets的差
• 上一步的矩阵平方，去掉负值
• 计算上一步的矩阵的平均值
  结果是一个值，叫做mean squared error（MSE).

#MSE Loss
def mse(t1,t2):
	diff=t1-t2
	return torch.sum(diff*diff)/diff.numel()
#Compute loss
loss=mse(preds, targets)
print(loss) #46194

torch.sum返回一个张量中所有元素的和。.numel返回张量中的元素数目。
loss值表示，平均来看，预测值的每一个元素与真实结果的差距为215（46194的开方）.loss越小越好。

计算梯度

PyTorch可以自动计算梯度或者loss的导数。之前的w， b的声明中需要设置requires_grad为True

# Compute gradients
loss.backward()

计算出来的梯度单独存在每个张量的 .grad中。所以w的grad依旧是跟w相同维度的矩阵。
loss是关于w和b的二次函数。我们的目的是让loss变小，所以通过求导，当导数为0时有可能就是最小值（不排除有多个极小值点，这时叫做局部最小值）
继续之前。我们需要用**.zero_()将梯度设为0。因为PyTorch会累计梯度。如果没有清零，下次使用.backward**时新的梯度值会加到原来的梯度值上。

# Reset the gradients
w.grad.zero_()
b.grad.zero_()
print(w.grad)
print(b.grad)

使用梯度下降来调整权重与偏差

步骤如下：

1. 生成preds
2. 计算loss
3. 计算梯度
4. 权重。偏差减去小比例的梯度值。（w-a*w.grad, 其中a为0-1之间的小数)
5. 将梯度设为0.

下面一步步实现

#Generate predictions
preds=model(inputs)

#Calculate the loss
loss=mse(preds, targets)

#Compute gradients
loss.backward()

#Adjust weights & reset gradients
with torch.no_grad():
	w-=w.grad*1e-5
	b-=b.grad*1e-5
	w.grad.zero_()
	b.grad.zero_()

注意：

• 使用torch.no_grad告知pytorch不要在更新weights， biases时计算修改梯度
• 之所以梯度乘1e-5是因为不想一下子更新太大步子
• 更新完了后设置w,b 为0

训练多个epoch

为了达到极小值，需要循环以上步骤来调整梯度。每一次迭代叫做一个epoch。

for i in range(100):
	preds=model(inputs)
	loss=mse(preds, targets)
	loss.backward()
	with torch.no_grad():
		w-=w.grad*1e-5
		b-=b.grad*1e-5
		w.grad.zero_()
		b.grad.zero_()

使用pytorch内置函数来线性回归

以上对矩阵的操作在pytorch中包装成了内置函数。
首先使用torch.nn

import torch.nn as nn

这次让输入集变大。

Dataset and DataLoader

首先新建一个TensorDataset，它允许以tuple访问inputs和targets里面的行。并提供标准API来处理各种类型的数据。

from torch.utils.data import TensorDataset
#Define dataset
train_ds=TensorDataset(inputs,targets)
train_ds[0:3]

结果返回tuple，(tensor(…), tensor(…))，第一个tensor为inputs， 第二个为targets。
Dataloader可以将数据分成预定大小的batch，还支持shuffling（打乱）和随机采样数据。

from torch.utils.data import DataLoader
batch_size=5
train_dl=DataLoader(train_ds, batch_size, shuffle=True)

使用for-in循环来访问data loader

for xb, yb  in train_dl:
	print(xb)
	print(yb)
	break

xb为batch_size大小的batch data。

nn.Linear

使用nn.Linear而不是手动初始化权重和偏差。

model=nn.Linear(3,2)
preds=model(inputs)

PyTorch使用**.parameters**来返回model中所有的权重和偏差矩阵。

list(model.parameters())

Loss Function

内置函数mse_loss来计算loss function

#Import nn.functional
import torch.nn.functional as F
# Define loss function
loss_fn=F.mse_loss
loss=loss_fn(model(inputs), targets)
print(loss)

nn.functional包包含了许多有用的loss funcions和其他工具

优化器

使用optim.SGD来更新参数。SGD全称stochastic gradient descent。stochastic意思是样本是从batchs中选出来的而不是从一个组中选出来的。

opt=torch.optim.SGD(model.parameters(), lr=1e-5)

训练

训练步骤与上面的一样。唯一不同的是现在是每次迭代处理batchs而不是整个训练集。定义函数fit，训练模型epoch次

def fit(num_epochs, model, loss_fn, opt):
	for epoch in range(num_epochs):
		for xb, yb in train_dl:
			pred=model(xb)
			loss=loss_fn(pred, yb)
			loss.backward()
			opt.step()
			opt.zero_grad()
		if (epoch+1)%10==0:
			print('Epoch [{}/{}], Loss:{:.4f}'.format(epoch+1, num_epochs, loss.item()))

**loss.item()**返回loss张量里存的真实值
训练完后对比发现预测值已经很接近真实值了。