论文阅读-3D Point Cloud Attribute Compression Using Geometry-Guided Sparse Representation

使用几何引导的稀疏表示的3D点云属性压缩

摘要

与属性关联的3D点云被认为是沉浸式通信的有希望的范例。但是，此媒介的相应压缩方案仍处于婴儿阶段。而且，与常规的图像/视频压缩相比，压缩由不规则结构引起的3D点云数据是更具挑战性的任务。在本文中，我们为体素化3D点云的属性提出了一种新颖有效的压缩方案。在第一阶段，将输入体素化3D点云分为大小相等的块。然后，为处理3D点云的不规则结构，提出了一种几何引导的稀疏表示（GSR），以消除每个块内的冗余，将其表示为l0范数正则化优化问题。而且，块间预测方案被应用以去除块之间的冗余。最后，通过GSR定量分析所得变换系数的特征，开发了一种针对我们的GSR量身定制的有效熵编码策略，以生成比特流。在各种基准数据集上的实验结果表明，与最新方法相比，所提出的压缩方案能够实现更好的速率失真性能和视觉质量。
索引词-3D点云，稀疏表示，不规则结构，预测编码，熵编码。

I.引言

随着3D感测技术的巨大进步，在实时条件下获取高度详细的3D点云变得越来越容易。完整的3D点云由一组指示点位置的3D坐标以及与每个点关联的一个或多个属性（例如颜色和法线）组成，可以灵活地表示3D对象和场景。 3D点云被广泛应用于许多领域，例如增强/虚拟现实，动画，游戏和自主导航，因为它们允许自由视点渲染，适应于表示复杂拓扑的对象并且计算效率高[2] 。 特别是，受益于渲染技术[3]和计算设备的进步，已经逐渐选择3D点云来表示3D对象和场景的表面以进行沉浸式通信，而不是3D网格来探索离散点之间的连通性[ 4] – [7]，导致较高的复杂度并引入了可能降低实时处理效率的伪像。
尽管3D点云有很多优点，但仍然存在一些基本问题，从而限制了此类3D点云数据的普及。 例如，通常3D点云包含数百万个点，从而导致海量数据。 因此，由于有限的网络带宽和存储空间[8]，[9]，迫切需要有效和高效的压缩方案。 不幸的是，对于以体积数据表示的这种新型沉浸式媒体，压缩仍处于起步阶段。 此外，与传统的图像/视频压缩相比，3D点云的压缩更具挑战性，因为它们是在3D空间中随机采样的，这使得许多成熟的传统图像/视频编码工具无法直接对其进行处理（例如， H.264 / AVC [10]和HEVC [11]）。
为了有效地压缩3D点云，自然可以考虑使用一些功能强大的工具来处理高维信号。 其中，稀疏表示已被证明可成功获取，表示和压缩高维信号。 在某种稀疏表示的情况下，信号被写入为仅来自预定基础或词典的几个原子的线性组合。 稀疏性原则在数据建模中起着重要作用，这是执行各种操作（如还原，压缩或解决反问题）的关键步骤。因此，利用信号在变换域或字典中的稀疏性的技术已在信号处理中广泛使用，从傅立叶变换，离散余弦变换（DCT）和小波变换到冗余字典[12]。 迫切需要将稀疏表示技术的最新进展引入3D点云，以解决上述问题和其他问题。 但是，这并不是一个直接的扩展，因为迄今为止，这些算法（例如DCT）主要用于处理在常规欧几里德空间（例如音频，图像和视频）中均匀采样的信号，而3D点云数据并未展示这样的特征[13]。
这篇文章中，针对体素化3D点云的属性，提出了一种有效的压缩方案。请注意，我们关心的是压缩3D点云的属性（例如颜色和法线），并且在不损失一般性的情况下，将颜色属性（在RGB或YUV颜色空间中）用作示例。该方法的主要新颖之处在于对3D点云数据的特殊特征（即不规则结构）的考虑。为此，对于首先划分为相等大小的块的输入体素化3D点云，我们提出了块间预测策略和几何引导的稀疏表示（GSR），分别减少了块间和块内冗余。通过利用GSR定量分析所得变换系数的特征，我们进一步设计了GSR量身定制的熵编码算法，该算法能够有效地将所得变换系数编码为比特流。大量的实验结果表明了其优越性。此外，值得注意的是，提出的压缩方案是我们先前工作的扩展[1]，它为嵌入在欧几里得空间中的不规则域上定义的不规则数据（例如3D点云的颜色）提供了稀疏表示。
本文的其余部分安排如下。 第二部分简要回顾了3D点云属性的现有压缩方案。 提议的压缩方案在第三节中介绍。 第四节进行了广泛的实验以及与最新方法的比较。 最后，在第五节中得出结论。

2.相关工作

在过去的几年中，已经提出了许多用于压缩3D点云数据的方法。 Schnabel和Klein [14]提出了一种渐进式压缩方法，该方法首次使用八叉树结构表示3D点云。 后来，基于八叉树的表示在[15]中进一步用于渐进点云压缩，在[8]，[16]中用于动态点云编码。受传统混合视频编码（例如H.264 / AVC [10]和HEVC [11]）的启发，Cohen 等人[17]提出了一种用于基于八叉树的3D点云的3D帧内预测方法，其中将相邻块中的重构属性投影到当前块的相邻边缘平面上，并将投影值用作参考。 但是，预测性能高度依赖于所占据体素的分布。 此外，还提出了基于变换的属性压缩方案。Mekuria等人[8]将颜色属性映射到具有深度优先八叉树遍历的2D网格，然后使用基于DCT的JPEG编解码器对属性进行编码。尽管该方法在点云属性压缩方面取得了一些进展，但它引入了阻塞效应(blocking effects)，并且压缩性能仍然受到限制。基于[8]，徐等[18]提出了一种包括八种扫描模式的自适应扫描方案。根据颜色属性编码的统计信息离线导出平衡速率和失真的拉格朗日乘数。随后从速率失真优化的意义上选择最佳模式。张等[19]应用图变换（GT）对属性进行解相关；也就是说，首先为3D块内的占用体素构建图，并通过反距离模型获得图拉普拉斯矩阵，其特征向量矩阵进一步用作变换矩阵。与基于DCT的编码器相比，GT可以实现更高的编码性能。但是，[19]中的点连接方法没有得到优化，从而导致了子图问题。为了解决这个问题，科恩等[20]应用k-最近邻（kNN）方法将不相交的点连接成一个图。但是，基于kNN的连接方法不能从根本上解决子图问题。后来，在[21]中提出了结合kd-tree结构和拉普拉斯稀疏优化GT的压缩框架。为了优化点云的分配，Zhang等人[22]开发了一种基于均值漂移的分层分割方法，其中进一步设计了集群内预测以减少每个集群中的冗余。邵等人[23]提出了一种基于切片的分层结构和基于块的帧内预测的混合点云属性压缩方案。 Queiroz和Chou [9]提出了一种区域自适应分层变换（RAHT），它是类似于Haar小波自适应变化的分层子带变换。与基于GT的压缩方案相比，基于RAHT的压缩方案具有更高的计算效率，同时可实现与GT相当的性能。为了进一步探索在不规则3D点云上定义的信号的统计数据，Queiroz和Chou [24]使用平稳的高斯过程对其进行建模，并提出了高斯过程变换（GPT）。
为了提高3D点云数据的压缩技术，在MPEG下成立了点云压缩（PCC）作为工作组，以开发新颖的解决方案来压缩3D几何和属性信息。 PCC小组致力于开发点云压缩标准，并在静态点云压缩，动态点云压缩和动态采集点云压缩方面取得了很大进展。 MPEG [25]发布的三个类别的相应测试模型分别是基于RAHT的TMC1，基于视频编码的TMC2和分层编码工具TMC3，其中TMC1和TMC3组合在一起成为TMC13 [26]。 最近，MPEG发布了其最新的测试模型[27]，其中包含两个配置文件，即V-PCC（基于视频编码）和G-PCC（基于本地3D编码）。

3.提出的压缩方案

我们假设3D点云的几何信息在颜色信息之前并与颜色信息分开进行编码和解码。 不失一般性，本文以颜色属性为点云属性的示例。

A.提出方案的概述

图1示出了所提出的方案的流程图，其主要包括三个阶段，即，块间预测，几何学指导的稀疏表示（GSR）和GSR定制的熵编码。更具体地说，如[8]，[17]，[19]，[28]中所建议，我们首先对非结构化3D点云采用基于体素的表示，即，在给定步长的情况下，将3D坐标量化为规则的和尺寸为2^L×2^L×2^L的轴对齐3D网格，其中L为级别(level)。如果体素至少包含一个点，则表示该体素已被占用。体素的几何形状是与体素角的3D坐标相对应的无符号整数三元组v∈R^3×1，并且属性是所包含点的属性的平均值。空的体素是透明的，没有其他属性。请注意，体素化的3D点云可以使用八叉树结构有效地组织和编码[14]，并且已经开发了用于生成和渲染此类数据的快速技术[3]。然后，我们将体素化的点云平均划分为大小为k×k×k的块（即每个块包含k×k×k个体素），并根据其3D位置对其进行组织。每个占用的块被认为是一个编码单元。对于每个块，使用块间预测策略预测其平均值，并将去除了平均值的颜色信号重新变形为一个向量，并进一步将其稀疏地表示为具有几何引导的稀疏表示的稀疏系数向量。以此方式，消除了块间和块内冗余两者。最后，使用GSR量身定做的熵编码算法将量化的预测残差和变换系数以及预测模式熵编码为比特流。

图一 提出的3D点云属性压缩方案的流程图

B.Inter-Block Prediction Strategy 块间预测策略

直观地，3D点云的相邻块对应于对象/场景的相似部分，指示它们之间的强相关性。 为了获得高压缩性能，应该充分利用这种块间一致性。 然而，块的体素被随机且不规则地占据，使得不可能直接借鉴传统视频编码的预测方案。 为此，我们提出了一种块间平均值的块间预测策略。
假设3D点云已被划分为m×m×m个块，并且每个块在3D空间中具有一个唯一坐标，表示为（p_x，p_y，p_z），其中1≤p_x≤m，1≤p_y≤m，并且 1≤p_z≤m。 图2（a）显示了8个相邻的块，其中位于（p_x，p_y，p_z）的灰色代表当前的编码单位，而位于（p_x - ^deltapx，p_y -^deltap_y，p_z − ^deltap_z），其中 ^deltap_x， ^deltap_y和 ^deltap_z∈{0，1}的其他7个有颜色的块是已编码的参考块。 注意，只有可以基于几何信息确定的占用块将用作参考块。

图二 块间平均值的块间预测策略插图。 （a）当前编码和参考块在3D空间中的相对位置。 这里，灰色块，即正面的右下角块，是用于编码的块，而其他彩色块是参考块。 （b）八个方向预测模式，第j个模式（j = 1，2，…，8）表示为block_j，它从第（j +1）个块中预测第一个块。 注意，块9的值是参考块2至8的平均值。
为了充分探究3D点云的相邻块内的基础相关性，所提出的块间预测策略设计了9种模式，即一种DC预测模式和8种定向预测模式，如图2（b）所示。对于当前块，DC预测模式意味着不需要预测，并且其平均值将被直接量化，而方向预测模式意味着仅在当前块的平均值与其参考块的平均值之间测得的预测残差 将被编码。具体地，block_j（1≤j≤8）指示第j个方向预测模式，其使用第（j + 1）个被占用的相邻块的平均值来预测当前块的平均值。 注意，将块9的值计算为块2到8的平均值。
所提出的块间预测策略的编码过程可以描述如下。 对于当前块，如果当前块的所有7个相邻块都未被占用，则将直接使用DC模式。 否则，将应用8种定向模式。 计算所有预测模式的预测残差（即，当前块和对应的参考块之间的差值），并且选择具有最小预测残差的预测残差作为最佳模式。 在上述步骤之后，利用算术编码算法对当前块的量化系数和相应的预测模式索引进行编码。

C. Geometry-Guided Sparse Representation (GSR) 几何引导的稀疏表示

如前所述，尽管稀疏表示（例如DCT，小波变换和冗余字典(redundant dictionaries)）已在各种应用中证明了其有效性，但它们主要用于处理在常规欧几里德空间（例如音频，图像和视频）中均匀采样的信号而且由于结构不规则，将它们扩展到3D点云并不容易。具体地，以图像为例，由于像素均匀地分布在规则的2D网格中，具有预定的色块大小√p×√p，因此可以将任意提取的色块分别重组为R^p×1中的矢量信号，然后在尺寸为R^p×1的基数/冗余字典(basis/redundant dictionary)上进行进行稀疏编码。但是，对于体素化的3D点云，尽管整个体素集位于规则的3D网格中，但所占据的体素集在空间中分布不均匀。 结果，在每个k×k×k体素块中，在占用的体素上定义的矢量信号的大小(dimensions)因块而异。

图三 提出的几何引导的稀疏表示的插图。 注意，仅可以使用几何数据来自适应地确定S_i。 由于几何数据是在颜色数据之前并与颜色数据分开进行编码和解码的，因此记录Si不需要任何开销。

为此，我们提出了几何引导的稀疏表示，如图3所示。我们将不规则特征视为由几何信息引导的虚拟自适应采样过程，即，

其中x_i∈R^ni×1由第i个块的已占用体素的颜色¹（在这里，我们仅考虑单个颜色通道，其他两个通道可以用相同的方式处理。）组成，y_i∈R^k^^3×1是一个虚拟信号，在假设第i个块的所有体素都被占用的情况下，包含所有体素的颜色。S_i ∈R^ni×k^³^（n_i<< k³）是下采样矩阵，即具有减少的行的单位矩阵，其对应于第i个块的未占用体素，并且n_i是第i个块中的占用体素的数量。注意，x_i的平均值等于0。通常，小块内的颜色平滑变化，即具有局部平滑特性。 它表示y_i为可压缩信号。 因此，我们进一步假设y_i可以通过满秩基础&∈R^k3×k3变换为近似稀疏系数c_i∈R^k3×1，即

此外，我们制定了一个优化问题来恢复系数：

其中N是占用块数，ε是控制c_i稀疏性的近似误差，||·||₀是向量的L₀范数，计算输入的非零元素数。 注意，仅可以使用几何数据来自适应地确定S_i，因此，不需要记录S_i的开销。 分别以S_i&为整体，即

我们可以看到Eq.(3)与过完备（或冗余）字典上的稀疏表示的众所周知的问题一致，字典的过完备可以为信号实现更灵活，更稳定，更鲁棒或更紧凑的表达。
为了实现稀疏表示的最佳性能，基础&的选择确实很重要。 如[1]中所建议的，考虑到GT可以很好地对属性进行去相关，我们在块的所有体素上采用GT的基本矩阵来实现&。 具体来说，我们首先使用反距离模型构造权重矩阵，即

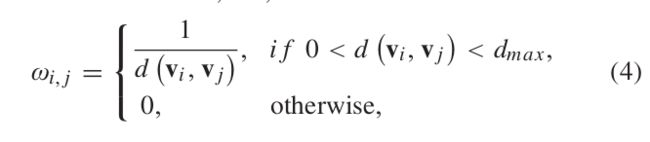
其中d(v_i, v_j)是两个体素之间的欧几里得距离，而d_max是一个阈值。 基于等式(4)可以推导一个拉普拉斯矩阵，其特征向量构成GT的基本矩阵。
为简单起见，我们采用了广泛使用的正交匹配追踪算法[30]来逐块求解方程(3)。 由于不同块的M项近似行为（即表示具有M个非零系数的信号时获得的误差或质量）可能不同，因此可以通过解拉格朗日形式的等式（3）来进一步改善稀疏性并通过乘法器的交替方向法求解它。
讨论：在这里，我们将直观地解释为什么使用压缩感测（CS）理论[31] – [33]提出的方法有效。
考虑稀疏或近似稀疏的向量α∈R^n×1。 令g =#α∈R^m×1（m<< n）是通过随机测量（或传感）矩阵#∈R^m×n进行的α的测量。 CS理论指出，如果限定的等距性质（RIP）成立对于#成立，那么可以通过求解下式获得α的重构：


另外，对(5)的解α帽对一些常数C服从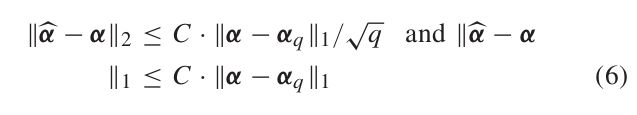
其中α_q是除最大q个元素（大小）之外的所有元素都设置为0的向量α。如果α是q稀疏的（即最多具有q个非零项q q，因此恢复准确。 如果α不是严格的q稀疏，则（6）断言所恢复的信号的质量就好似一个人提前知道q的位置，α的最大值并决定直接对其进行测量。
根据CS理论[32]，我们可以得出结论，如果RIP保持S_i&不变，则优化的稀疏系数c_i可以很好地表示y_i，也可以表示x_i，因为x_i是y_i的子集。此外，我们只关心xi是否可以代替yi来很好地表示，这与CS恢复未知原始信号的目标不同，因此，尽管RIP在实践中不能完全满足要求，但可以期望（3）中有更多的稀疏系数。

D. GSR Tailored Entropy Coding Algorithm GSR量身定制的熵编码算法

现有的压缩方案[9]，[19]，[24]假定变换系数遵循一定的拉普拉斯分布，然后使用算术编码和自动估计的概率分布函数将其编码为比特流。这种方法的优点是不需要存储/传输概率表来节省位。但是，这种方法不适用于我们提出的GSR。原因是GSR是一个过完整的变换(overcomplete transform)，将生成很多零系数。如果我们使用拉普拉斯分布熵对稀疏系数进行熵编码，则将消耗许多位来表示零系数，这将大大降低压缩性能。为了证明我们的主张的正确性，我们进行了M项(M-term)近似实验，其中M的值通过占用的体素数归一化并表示为p_c，重建质量通过峰值信噪比（PSNR）进行测量。提出的GSR以及RAHT [9]，[29]的相应结果显示在表I中，我们可以观察到，即使在较高的重建质量下，提出的GSR也会产生非常稀疏的系数，例如，当重建质量比Soldier高44.18 dB时，非零系数只有3.18％。此外，在相同的重建质量下，变换系数比RAHT稀疏得多，这表明我们提出的GSR具有出色的去相关能力。
基于这些观察结果以及众所周知的Run-Level编码算法（经常用于具有许多连续相同元素的序列）的启发，我们提出了GSR量身定制的熵编码算法来对量化的变换系数进行编码，如图4所示。我们用两个一维单元格数组来表示量化系数，即Run和Level，分别记录非零系数及其值的索引差。由于非零系数的数量逐块变化，因此我们引入了语法Num（向量）来计算每个块中非零系数的数量。更具体地，如果在第i个量化系数矢量α_i中存在N_i个非零系数，则我们分别有Num [i] ＝ N_i，Run {i} ＝ run_i和Level {i} ＝ level_i，其中run_i是α_i中非零系数的索引差(index difference)，level_i代表α_i中非零系数的值。如果α_i中没有非零系数，则我们仅将零存储到Num [i]，而不会将任何内容写入Run {i}和Level {i}。处理完所有块后，将使用算术算法对三个变量Num，Run和Level进行熵编码。

表1 提出的GSR和RAHT在M术语近似中的比较。 p_c是Nonzero转换系数的百分比。 注意，将p_c(％)计算为nonzero系数数量与所占体素数之比。 PSNR和pc的值对应于三个彩色通道的平均值。

图4 提出的GSR量身定做的熵编码算法的流程图，用于量化变换系数。

IV. EXPERIMENTAL RESULTS AND DISCUSSION 实验结果和讨论

在本节中，将进行大量实验以评估建议的压缩方案。 我们的实验包括：（1）块大小和块间预测对性能的影响； （2）所提方案与两种最新的点云属性压缩方法（即RAHT [9]，[29]和MPEG最新的测试模型G-PCC [34]）之间的速率失真性能，视觉质量和计算复杂度的比较 。 请注意，作者提供的RAHT的新源代码可以从https://github.com/digitalivp/RAHT下载。

A. Datasets and Implementation Details 数据集和实施细节

在我们的实验中，使用了15个基准3D点云数据集，因为它们广泛用于各种点云压缩方法的性能评估中[9]，[21]，[24]，[29]，[35]。 其中九个是从实时数据库Microsoft Voxelized Upper Bodies（MVUB）[36]和8i Voxelized Full Bodies（8iVFB）[37]的动态点云序列中提取的帧。
它们是安德鲁，大卫，里卡多，菲尔，莎拉，朗德夫斯，战利品，士兵和雷德黑德(Andrew, David, Ricardo, Phil, Sarah, Longdress, Loot, Soldier and Redandblack,)，它们分别提取的帧索引分别为27、1、39、244、18、1、1、1、101。 其余使用的点云数据集为Frame_0200，Egyptian_mask_vox12，Shiva_00035_vox12，Facade_00009_vox12，House_without_roof_00057_vox12和Frog_00067_vox12(由于最后五个数据集都很稀疏，因此我们以9和10的深度对它们进行了重新体素化)，它们从静态对象和场景数据库[34]的测试类A中选择。 上述15个点云数据集的说明可参考图5。

图5 在特定视图中渲染的测试3D点云：（a）Andrew； （b）David； （c）Ricardo； （d）Phil； （e）Sarah； （f）Longdress； （g）Loot； （h）Soldier； （i）Frame_0200； （j）Redandblack； （k）Egypt_mask_vox12； （l）Shiva_00035_vox12; （m）Facade_00009_vox12; （n）House_without_roof_00057_vox12; （o）Frog_00067_vox12。
块预测中的统一量化步长设置在2到20之间，变换系数的步长在4到80之间变化。此外，ε的值范围在4到150之间。参考实验[1]中的结果，在dmax等于1的情况下，GSR可以达到几乎最佳的性能。
常用的评估标准，它以每个点的三个分量（即Y，U和V）的比特率（即每个顶点的比特数，bpv）来衡量速率，并以PSNR的形式衡量失真的分量的dB率。并通过使用MPEG PCC PSNR工具[38]来计算PSNR。 此外，还使用了传统视频编码中常用的评估标准Bjøntegaarddelta PSNR（BD-PSNR）（以dB为单位）和Bjøntegaarddelta比特率（BD-BR）（以百分比为单位）[39]，[40] 测量两种方法的速率失真性能之间的平均PSNR和比特率差异。

B.块大小对性能的影响

在点云分区中，块大小决定了块中包含的体素数量。 现有的所有压缩方法都使用通用的块大小，而忽略了对块大小对性能的影响的分析。 为此，我们研究了具有不同块大小k（即8、10和12）的压缩方案的性能。 相应的实验结果示于表Ⅱ。 图6进一步举例说明了点云Loot，Soldier，Andrew和David的速率失真曲线。 从表II和图6可以很容易地观察到，性能随着块大小的增加而提高。 这是因为较小的块大小将破坏点云中继承的相关性。 但是，较大的块大小将显着增加计算复杂度。 为了在压缩性能和计算复杂度之间取得良好的折衷，在这项工作中使用了块大小k = 12。

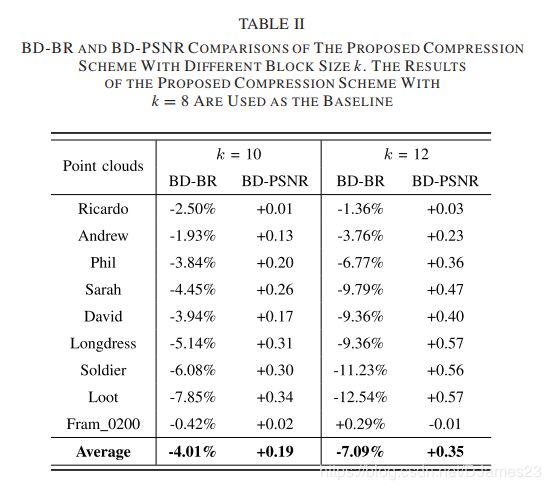
表2 使用不同块大小k的提出的压缩方案的BD-BR和BD-PSNR比较。 以k = 8的提议压缩方案的结果作为基准。

图6 块大小k对速率失真性能的影响的示意图。

C.验证提出的块间预测策略的有效性

为了验证所提出的块间预测策略的有效性，单独评估了具有/不具有块间预测策略的所提出的压缩方案。 注意，所提出的没有块间预测策略的方法是直接对量化的平均颜色值进行编码。 相应的结果示于表III。 可以看到，与没有块间预测的方法相比，具有块间预测策略的所提出的方法能够实现更好的性能（即，平均地，0.21 BD-PSNR改善和3.71％BD-BR降低）。 图7还以Loot，Soldier，Andrew和David的点云的速率-失真曲线为例，从中我们还可以得出结论，提出的块间预测方案可以极大地提高编码效率。

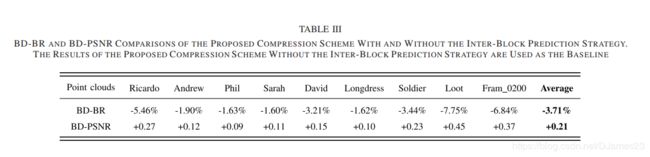
表3 带有或不带有块间预测策略的建议压缩方案的BD-BR和BD-PSNR比较。 没有块间预测策略的提议压缩方案的结果用作基准。

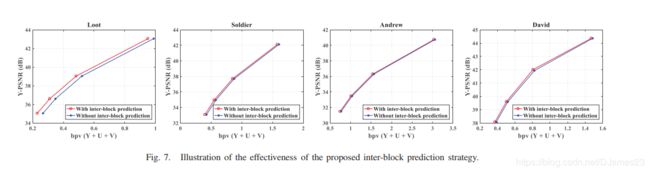
图7 提出的区块间预测策略有效性的展示

D.速率失真性能比较

就15个点云数据集的速率失真性能而言，我们将提出的方法与两种最先进的方法进行比较，即RAHT [9]，[29]和G-PCC [34]。 相应的结果显示在表IV和图8中，我们可以得出以下结论：
1.总体而言，与RAHT和G-PCC相比，我们的方法将所有15个测试数据集的平均BD-BR分别降低了20.33％和10.26％，并将平均BD-PSNR分别提高了1.25 dB和0.60 dB，验证了我们提出的方法相对于RAHT和G-PCC的显着优势；
2.对于除Frame_0200以外的所有十个半/全人体数据集，我们的方法始终比RAHT和G-PCC均获得更好的速率失真性能。 从数量上讲，我们的方法分别使BD-PSNR平均增加1.79 dB和1.09 dB，以及BD-BR平均减少28.85％和18.81％。 这样的显着优势归功于所提出的GSR，块间预测策略和量身定制的熵编码算法能够很好地适应不规则数据，以利用3D点云数据中继承的冗余。
3.对于五个物体数据集，我们的方法的性能比RAHT稍好，但比G-PCC稍差。更具体地说，我们的方法可将BD-PSNR平均提高0.18 dB和-0.38 dB，将BD-BR降低3.29％和-6.83％。原因如下。首先，这五个物体数据集的特征与十个人体数据集的特征完全不同。也就是说，它们严重嘈杂，并且包含大量漏洞(holes)。其次，我们的方法假设一个小块内的颜色变化平稳，因此可以采用一个过完整(over-complete dictionary )的字典来很好地表示只有几个原子的颜色。所采用字典的冗余属性还导致非零变换系数的潜在位置的范围更大。如果存在大量非零系数，则用于编码其位置的比特成本（即，熵编码模块的Run分量）将是巨大(heavy)的。同时，这些数据集的噪声特征将导致许多小幅度的非零系数，这使得用于编码其位置的位比用于编码幅度的位（即，熵编码模块的Level分量）更重要。因此，此类数据集的总体速率失真性能将受到影响。然而，RAHT和G-PCC采用类似Haar的正交变换，这不适用于信号统计[24]，因此它们在这些数据集上仍然运行良好。

表4 提出的压缩方案与Raht和G-PCC的BD-BR和BD-PSNR比较


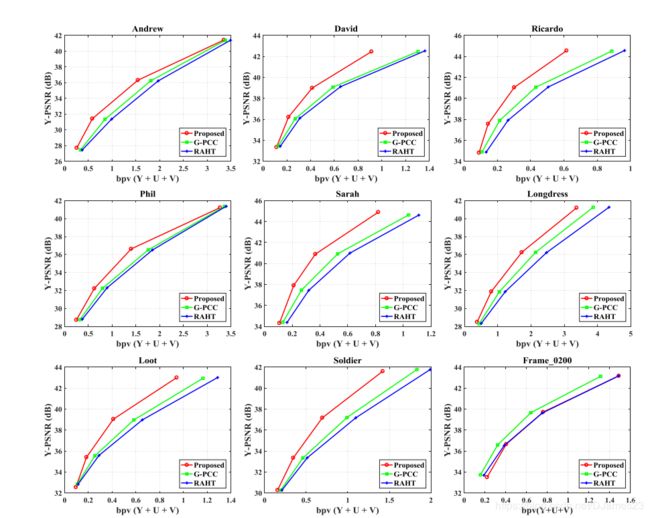
图8 在15个基准数据集上，所提出方案与两种最先进的方法，即RAHT和G-PCC的速率失真性能的比较

E.视觉质量比较

此外，图9和图10分别以点云数据“Ricardo”和“Loot”为例，显示了所提出的方法与两种最新的3D点压缩方法之间的视觉质量比较。 为了更好地说明，在这两个点云数据中由红色边框表示的放大区域被放大并显示。

图9 来自不同的方法的“Ricardo”解码点云的视觉比较。 每种方法列出了每个体素的比特和PSNR

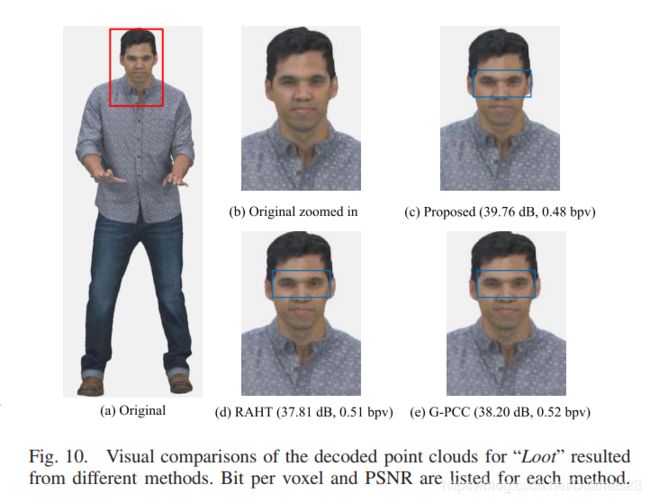
图10 来自不同的方法的“Loot”解码点云的视觉比较。 每种方法列出了每个体素的比特和PSNR
可以看到，通过RAHT [9]，[29]和G-PCC [34]重建的点云包含明显的噪声/模糊，例如，图9(d)和(e)中蓝色边界框指示的区域。与RAHT和G-PCC相比，该方法能够以相当的比特数获得更好的视觉质量（例如，在无纹理的区域更平滑，边缘更锐利），并且重构的点云更接近原始云。

F.计算复杂度的分析

在我们提出的压缩方案中，特征分解仅执行一次即可构建矩阵&，该矩阵将用于3D点云中的所有已占用块。 而我们方法的复杂性主要由GSR模块中的OMP算法决定。 更具体地说，对于包含N个占用块的点云，OMP算法的计算复杂度为

其中n_i和q_i分别是第i个块中占用的体素数和非零系数的数量，k是块的大小。
为了定量评估计算复杂度，我们比较了我们的方法和G-PCC在每个3D点云上的运行时间，并在表V中显示了相应的结果。用于进行这些实验的PC由3.10 GHz Intel Core i5-4440处理器和12 GB内存组成，而我们的方法是使用MATLAB 2016b实现的。 考虑到G-PCC是用C ++实现的，因此很难直观地感知我们的方法与G-PCC之间的差距，因此，我们还提供了早期MPEG测试模型TMC1的编码和解码时间[35]，该模型是通过MATLAB实现的并与G-PCC共享相同的核心技术（或基本框架）作为参考。 请注意，G-PCC仅输出包括编码和解码过程在内的总体运行时间。

表5 提出的压缩方案与TMC1和G-PCC编码和解码时间比较（第二）
从表V中可以看出：（1）我们的方法在15个数据集上的平均编码时间是TMC1的两倍以上。 原因在于，所提出的方法需要通过贪婪算法greedy algorithm（即，OMP）来解决具有过完备字典的稀疏表示，这很费时； （2）我们的方法的解码时间比TMC1的稍长，因为我们的方法必须在解码时根据每个块的几何信息构造字典； （3）G-PCC比我们的方法和TMC1都快得多。 我们认为，G-PCC的如此重要优势主要是通过采用的C ++平台带来的。 将来，我们将继续研究加速编解码器的方法，例如，采用高级算法来解决稀疏表示，并开发算法来自动删除字典中高度相关的原子以减小字典大小。

5.结论

在本文中，我们针对3D点云数据的属性提出了一种新颖有效的压缩方案。 为了充分利用此类不规则数据的冗余性，我们提出了几何引导的稀疏表示（GSR）和块间预测策略。 另外，提供了GSR量身定做的熵编码算法，以将所得的变换系数有效地编码为比特流。 实验结果表明，该方案在速率失真性能方面优于最新方法，即我们的方案实现了BD-PSNR的平均改善，超过0.60 dB，而在15个基准数据集中，降低了10％以上的平均BD-BR。 我们认为，可以通过研究更高级的预测策略和更有效的变换基础矩阵来进一步改善我们的方案，这些将作为我们未来的工作。