计算机底层二进制

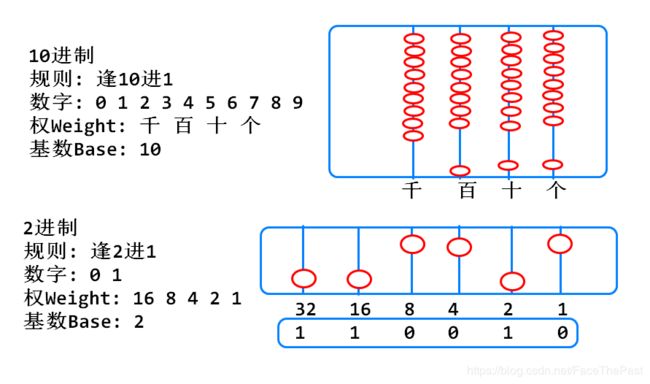
2进制

---

什么是2进制：逢2进1的计数规则.

10进制 与 2进制：

案例:

public static void main(String[] args) {
    /*
     * 2进制
     */
    //编译时候 将10进制"50"转换为2进制
    //软件运行期间, i在内存中是2进制
    int i = 50;
    /*
     * toBinaryString 将整数i在内存中
     * 存储的2进制实际位数转换为字符串
     * 如需要展示一个整数在内存中实际
     * 的2进制情况时候就调用这个方法
     */
    System.out.println(
            Integer.toBinaryString(i));
    /* 
     * i在内存中就是2进制的 110010 
     * 而println方法在输出时候自动
     * 调用了 Integer.toString() 
     * 将2进制转换为10进制字符串,
     * 最终输出了十进制字符串 "50" 
     */
    System.out.println(i);//50

    for(i=0; i<=150; i++) { 
        System.out.println(
            Integer.toBinaryString(i));
    }
}

因为高位0被省略了,所以实际输出结果应该为:

00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000001
00000000 00000000 00000000 00000010
00000000 00000000 00000000 00000011
00000000 00000000 00000000 00000100
00000000 00000000 00000000 00000101
00000000 00000000 00000000 00000110
00000000 00000000 00000000 00000111
00000000 00000000 00000000 00001000
00000000 00000000 00000000 00001001
00000000 00000000 00000000 00001010
00000000 00000000 00000000 00001011
00000000 00000000 00000000 00001100
00000000 00000000 00000000 00001101
00000000 00000000 00000000 00001110
00000000 00000000 00000000 00001111

Java编程语言解决了人类与计算机沟通问题:

16进制

---

16进制用于简写(缩写)2进制!

1. 2进制直接书写冗长,繁琐,易错很不方便
2. 16进制的基数是2进制基数的4次幂
3. 简写规则: 2进制数字从低位到高位,每4个2进制数可以缩写为一个16进制数.

原理:

案例:

public static void main(String[] args) {
    /*
     * 16进制用于简写2进制
     */
    // Java 7 提供了 0b前缀用于声明
    // 2进制直接量
    int n = 0b110010; //50
    int m = 0b101101011110001001111101010101;
    //m可以缩写为i
    int i = 0x2d789f55;

    System.out.println(m==i);
    System.out.println(
            Integer.toBinaryString(m));
    System.out.println(
            Integer.toBinaryString(i));

}

补码

---

为了解决"负数"问题,将固定位数的2进制数,分一半作为"负数"使用的编码规则,称为补码.

补码的核心目的是解决 “负数” 的编码问题.

1. 计算机底层硬件不支持"负数"
2. 利用补码编码规则实现"负数",“负数的计算”

补码是如何编码的:

1. 以4位数编码为例讨论补码编码规则
2. 4位补码没有实用价值
3. 补码规则可以推广到32位int数
4. 4位2进制计算时候,要保持4位数不变,多出的位数自动溢出
5. 高位为0的作为正数, 值就是原始的2进制值
6. 高位为1的作为负数, 从0倒推编码

都是1的数是-1
一个1以后都是0的数是最小值

7. 因为高位可以判断正负数,所以称为是"符号位"
8. 补码正负数互补对称(巧合): -n=~n+1

原理:

案例:

public static void main(String[] args) {
    /*
     * 补码的编码规律
     */
    int max = Integer.MAX_VALUE;
    int min = Integer.MIN_VALUE;
    System.out.println(
            Integer.toBinaryString(max));
    System.out.println(
            Integer.toBinaryString(min));
    System.out.println(
            Integer.toBinaryString(max+1));
    System.out.println(min);
    System.out.println(max);


    long lmax = Long.MAX_VALUE;
    long lmin = Long.MIN_VALUE;
    System.out.println(
            Long.toBinaryString(lmax));
    System.out.println(
            Long.toBinaryString(lmin));

}

经典面试题目:

System.out.println(~-8);
如上代码输出结果是( B ): A.6 B.7 C.8 D.9

2进制运算

---

运算符:

~ & | >>> >> <<

与运算 & (and)
基本规则(逻辑乘法), 有0则0

0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1

计算时候需要将两个数对其位置, 对应的位进行与计算

举个栗子:

n =    01110111 11010010 10111000 10111010
m =    00000000 00000000 00000000 11111111
k=n&m  00000000 00000000 00000000 10111010

如上案例的意义: k中的数据是n数据的最后8位数, 相当于将n的最后8位数切下存储到了k中. 如上计算称为"掩码计算",其中用于拆分数据的工具m称为 “掩码Mask”, 8个1称为8位掩码.

案例:

int n = 0x77d2b8ba;
int m = 0xff;
int k = n & m;
System.out.println(
    Integer.toBinaryString(n));
System.out.println(
    Integer.toBinaryString(m));
System.out.println(
    Integer.toBinaryString(k));

右移位计算 >>>
运算规则: 将2进制数整体向右移动, 低位多出数字溢出舍弃, 高位补0.

举个栗子:

n =     01110111 11010010 10111000 10111010
m=n>>>1 001110111 11010010 10111000 1011101 
k=n>>>2 0001110111 11010010 10111000 101110
g=n>>>8 00000000 01110111 11010010 10111000
b3=(n>>>8) & 0xff;

案例:

int n = 0x77d2b8ba;
int m = n>>>1;
int k = n>>>2;
int g = n>>>8;
int b3 = (n>>>8) & 0xff;
//按照2进制输出 n m k g b3

将一个整数拆分为4个byte
案例:

public static void main(String[] args) {
    /*
     * 将整数拆分为 4个byte
     * raf.writeInt()方法的底层就是
     * 利用2进制计算将int拆分为4个byte
     * 然后写到文件中.
     */
    int n = 0x77d2b8ba;
    int b1 = (n>>>24) & 0xff;
    int b2 = (n>>>16) & 0xff;
    int b3 = (n>>>8) & 0xff;
    int b4 = n & 0xff;
    System.out.println(
            Integer.toBinaryString(n));
    System.out.println(
            Integer.toBinaryString(b1));
    System.out.println(
            Integer.toBinaryString(b2));
    System.out.println(
            Integer.toBinaryString(b3));
    System.out.println(
            Integer.toBinaryString(b4));
}

| 或计算
基本规则(逻辑加法), 有1则1

0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1

将两个2进制数对齐位数,对应位进行或计算.

举例子:

n =   00000000 00000000 00000000 10110111
m =   00000000 00000000 10111110 00000000
k=n|m 00000000 00000000 10111110 10110111 

如上代码的意义: 将两个8位数拼接在一起

b1 =   00000000 00000000 00000000 11001110
b2 =   00000000 00000000 00000000 10111010
b3 =   00000000 00000000 00000000 11110110
b4 =   00000000 00000000 00000000 10001101

b1<<24 11001110 00000000 00000000 00000000 
b2<<16 00000000 10111010 00000000 00000000
b3<<8  00000000 00000000 11110110 00000000 
b4     00000000 00000000 00000000 10001101

n = (b1<<24)|(b2<<16)|(b3<<8)|b4;

案例:

int n = 0xb7;
int m = 0xbe00;
int k = n|m;
int b1 = 0xce;
int b2 = 0xba;
int b3 = 0xf6;
int b4 = 0x8d;
int i = (b1<<24)|(b2<<16)|(b3<<8)|b4;
//验证: 输出n m k b1 b2 b3 b4 i 的2进制

1. 2进制数字向左移动一次, 数值扩大两倍
2. 2进制数字向右移动一次, 数值缩小两倍

案例:

int n = 50;
int m = n<<1;//100
int k = n<<2;//200
int g = n<<3;//400

栗子:

n =     00000000 00000000 00000000 00110010 50
m=n>>1  000000000 00000000 00000000 0011001 25
k=n>>2  0000000000 00000000 00000000 001100 12
a=n>>>1 000000000 00000000 00000000 0011001 25
b=n>>>2 0000000000 00000000 00000000 001100 12

n =     11111111 11111111 11111111 11001110 -50
m=n>>1  111111111 11111111 11111111 1100111 -25 
k=n>>2  1111111111 11111111 11111111 110011 -13
a=n>>>1 011111111 11111111 11111111 1100111 2147483647-24  

ArrayList 扩容规则: 每次扩充1.5倍 = n + n>>1 = n + n/2

int oldCapacity = elementData.length;
int newCapacity = oldCapacity + (oldCapacity >> 1);

经典面试题目:

可以将 n * 8 优化为( n<<3 )
可以将 n / 2 替换为( n>>1 ), n是大于0的数

i=i++

---

栗子:

int i = 5;
i = i++;
System.out.println(i); //5

i = 5;
System.out.println(i++); //5
System.out.println(i);//6

i=i++ 的计算步骤分析: