tensorflow2.0实现鸢尾花数据集的分类(3)——激活函数
1.谜题揭晓
在上一篇博客:
tensorflow2.0实现鸢尾花数据集的分类(2)——神经网络搭建
笔者在结尾留了一个问题,今天我们就来解释一下
我们搭建神经网络比较重要的一步是前向传播,这一步少了一点东西,我们是这样做得:
with tf.GradientTape() as tape:
#前向传播计算 y, y为预测结果
y = tf.matmul(x_train, w) + b
# 计算损失函数
loss = (y - y_train)**2
loss = tf.reduce_mean(loss, axis=0)
你可能会说,对啊,这没错啊,神经网络模型不就是: y = x ∗ w + b y = x*w + b y=x∗w+b,这么做有什么错吗??
那我再举一个例子:如果搭建两层神经网络:
y 1 = x ∗ w 1 + b 1 ( 1 ) y 2 = y 1 ∗ w 2 + b 2 ( 2 ) y_1 = x*w_1 + b_1\qquad(1)\\ y_2 = y_1 * w_2 + b_2\qquad(2) y1=x∗w1+b1(1)y2=y1∗w2+b2(2)
那么模型的表达力一定会增强吧?!
答案是否定的
将式 ( 1 ) (1) (1)带入式 ( 2 ) (2) (2)中,你会发现:
y 2 = y 1 ∗ w 2 + b 2 = ( x ∗ w 1 + b 1 ) ∗ w 2 + b 2 = x ∗ ( w 1 ∗ w 2 ) + ( b 1 ∗ w 2 + b 2 ) \begin{aligned} y_2 &= y_1 * w_2 + b_2\\ &= ( x*w_1 + b_1) * w_2 + b_2\\ &=x * (w_1 * w_2) + (b_1 * w_2 + b_2) \end{aligned} y2=y1∗w2+b2=(x∗w1+b1)∗w2+b2=x∗(w1∗w2)+(b1∗w2+b2)
这本质上还是我们原来的模型 y = x ∗ w + b y = x*w + b y=x∗w+b,可以很容易的想到,无论经过多少层神经元,最后的模型依然是 y = x ∗ w + b y = x*w + b y=x∗w+b,所以模型表达力并不会有很大的提升。
现在终于可以揭晓答案了,原因是,我们的"神经网络"模型,其实仍然是个线性模型,因为无论多少层,其最终化简依然是线性模型!而线性模型的不能够表达非线性的部分
那我们怎样做才能将模型非线性话呢?对的,就是引入非线性的激活函数
2.激活函数特点
早在1943年提出的MP模型 y = f ( x ∗ w + b ) y = f(x*w + b) y=f(x∗w+b) 中,就已经提出引入非线性函数 f f f:

而就是由于非线性函数的加入,使得输出 y y y不再是输入 x x x的线性组合,神经网络可以随着层数的增加提示表达力!
我们之前一定听说过, r e l u relu relu激活函数和 s i g m o i d sigmoid sigmoid激活函数,那他们这么有名,是具备了什么优秀的性质呢??
- 非线性: 只有激活函数非线性时,才不会被单层网络所替代,多层神经网络可逼近所有函数
- 可微性: 优化器大多用梯度下降更新参数 ,若激活函数不可微,则无法更新参数
- 单调性: 当激活函数是单调的,能保证单层网络的损失函数是凸函数
- 近似恒等性: 有 f ( x ) ≈ x f(x)\approx x f(x)≈x,当参数初始化为随机小值时,神经网络更稳定
在今后的实践中,我们可以通过以上性质来寻找属于自己模型的激活函数!
3.常用激活函数介绍
(1). S i g m o i d Sigmoid Sigmoid函数
- 表达式: f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
- tensorflow API :
tf.nn.sigmoid(x) - 函数图像:
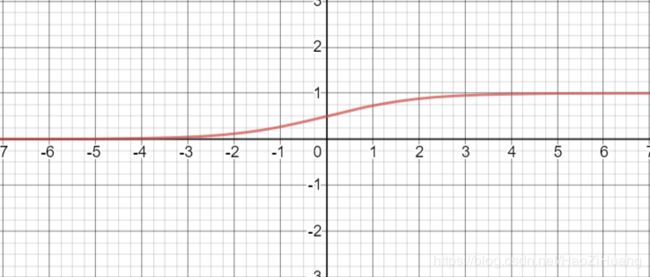
- 导数图像:

- 重要特点:
- s i g m o i d sigmoid sigmoid将输入变为0到1的值,相当于对输入进行了归一化
- 容易造成梯度消失,因为在更新参数时,需要从输出层到输入层进行链式求导,而我们可以从导数图线看出其导数值的范围是0到0.25,所以在进行链式求导时,需要多个0到0.25的数字相乘,容易造成梯度消失,使得参数无法继续更新(可以看做存在饱和( S a t u r a t e d Saturated Saturated)现象)
- 输出的均值非0,收敛慢,我们希望输出是以0为均值的,而其输出为0到1使得收敛变慢
- 存在幂运算,计算复杂度大,训练时间长
(2). T a n h Tanh Tanh函数
- 表达式: f ( x ) = 1 − e − 2 x 1 + e − 2 x f(x)=\frac{1-e^{-2x}}{1+e^{-2x}} f(x)=1+e−2x1−e−2x
- tensorflow API :
tf.math.tanh(x) - 函数图像:

- 导数图像:
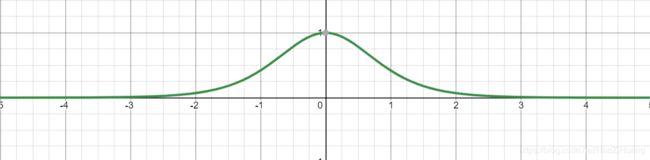
- 重要特点:
- 输出均值为0
- 仍然易造成梯度消失(可以看做存在饱和现象)
- 含有幂运算,训练时间长
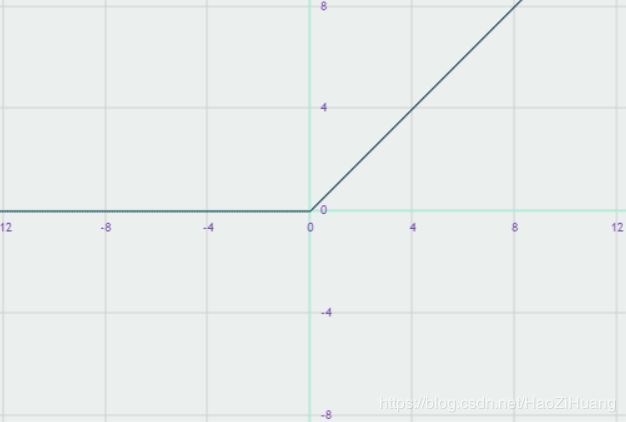
(3). r e l u relu relu函数
- 表达式: f ( x ) = m a x { x , 0 } = { x x ⩾ 0 0 x < 0 \begin{aligned} f(x)&=max\{x, 0\}\\ &=\left\{\begin{matrix} x \qquad x\geqslant 0 \\ 0 \qquad x<0 \end{matrix}\right. \end{aligned} f(x)=max{x,0}={xx⩾00x<0
- tensorflow API :
tf.nn.relu(x) - 函数图像:
- 导数图像:
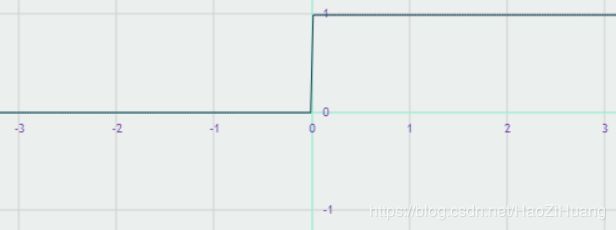
- 重要特点:
- 在正区间内解决了梯度消失问题
- 计算速度快,只需要解决输入是否大于0
- 收敛速度快于 s i g m o i d sigmoid sigmoid和 t a n h tanh tanh
- 输出均值非0
- 存在 D e a d r e l u Dead\ relu Dead relu问题,即送入激活函数的特征是负数时,激活函数输出是0,反向传播得到的梯度为0,导致参数无法更新,造成神经元死亡
(4). l e a k y r e l u leaky\ relu leaky relu函数
- 表达式: f ( x ) = m a x { x , a x } = { x x ⩾ 0 a x x < 0 \begin{aligned} f(x)&=max\{x, ax\}\\ &=\left\{\begin{matrix} x \qquad x\geqslant 0 \\ ax \qquad x<0 \end{matrix}\right. \end{aligned} f(x)=max{x,ax}={xx⩾0axx<0
- tensorflow API :
tf.nn.leaky_relu(x) - 函数图像:

-导数图像

- 重要特点:
理论上来讲, L e a k y R e L U Leaky\ ReLU Leaky ReLU有 R e L U ReLU ReLU的所有优点,外加不会有 D e a d R e L U Dead\ ReLU Dead ReLU问题,但是在实际操作当 中,并没有完全证明 L e a k y R e L U Leaky\ ReLU Leaky ReLU总是好于 R e L U ReLU ReLU。
4.更改神经网络:
with tf.GradientTape() as tape:
#前向传播计算 y, y为预测结果
y = tf.matmul(x_train, w) + b
y = tf.nn.softmax(y) # <-------------------------在此处加入激活函数即可,没错,就加一句代码
# 计算损失函数
loss = (y - y_train)**2
loss = tf.reduce_mean(loss, axis=0)
加上激活函数,再去训练你的模型试试准确率,应该能达到 95 % 95\% 95%以上
5.感谢在线绘图网站:
https://www.desmos.com/calculator
注:在该网站还可以画分段函数,如绘制 r e l u relu relu函数:
{ x > 0 } x { x < 0 } 0 \{x>0\}\ x\\ \{x<0\}\ 0 {x>0} x{x<0} 0