Leetcode 115. 不同的子序列
题目
给定一个字符串 S 和一个字符串 T,计算在 S 的子序列中 T 出现的个数。
一个字符串的一个子序列是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,“ACE” 是 “ABCDE” 的一个子序列,而 “AEC” 不是)
示例 1:
输入: S = “rabbbit”, T = “rabbit”
输出: 3
解释:
如下图所示, 有 3 种可以从 S 中得到 “rabbit” 的方案。
(上箭头符号 ^ 表示选取的字母)
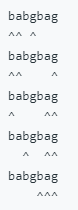
示例 2:
输入: S = “babgbag”, T = “bag”
输出: 5
解释:
如下图所示, 有 5 种可以从 S 中得到 “bag” 的方案。
(上箭头符号 ^ 表示选取的字母)
解答
解法一:回溯法
不计较效率的话,其实可以使用回溯法解决。
虽然会 TLE ,但是使用回溯法也是有其优势的!
它可以获得结果集里每一个子序列是由哪些下标组成的,而不仅仅只得到数量。
如果换个题目要求获得所有(子序列的下标组成),那么使用回溯法就再合适不过了。
代码
class Solution {
private int n = 0;
public int numDistinct(String s, String t) {
backtrace(s.toCharArray(), 0, t.toCharArray(), 0);
return n;
}
private void backtrace(char[] w1, int index1, char[] w2, int index2) {
if(index2 == w2.length) {
n ++;
return;
} else {
for(int j = index1; j < w1.length - (w2.length - index2) + 1; j ++) {
if(w1[j] != w2[index2]) continue;
backtrace(w1, j + 1, w2, index2 + 1);
}
}
}
}
结果
解法二:动态规划
仅仅获得数量的话,可以使用动态规划的方式,因为本题具有最优子结构。
动态规划四要素:
- 状态定义:dp[i][j] 表示 t 字符串的前 i 个字符与 s 字符串的前 j 个字符能产生的子序列数量。
- 状态转移:
- 如果 t[i] == s[j] 有两种情况:
- 使用 s 的第 j 位置字符:dp[i - 1][j - 1]
- 不使用 s 的第 j 位置字符:dp[i][j - 1]
- 否则 t[i] != s[j]:其实相当于不使用 s 的第 j 位置字符,dp[i][j - 1]
- 如果 t[i] == s[j] 有两种情况:
- 初始化:dp[0][j] = 1
- 结果:dp[t.length()][s.length()]
一个示例的 dp 数组的二维值图:

复杂度:O(nm) 时间, O(nm) 空间 。
常规动规代码
class Solution {
public int numDistinct(String s, String t) {
int[][] dp = new int[t.length() + 1][s.length() + 1];
Arrays.fill(dp[0], 1);
for(int i = 1; i <= t.length(); i ++) {
for(int j = 1; j <= s.length(); j ++) {
if(s.charAt(j - 1) == t.charAt(i - 1)) {
dp[i][j] = dp[i][j - 1] + dp[i - 1][j - 1];
} else {
dp[i][j] = dp[i][j - 1];
}
}
}
return dp[t.length()][s.length()];
}
}
结果
优化代码一:行主序
如果将二维数组 dp 中 s 串的一行记录作为行值,O(nm) 空间可以优化成一维数组的 O(n) 空间。
但每一次动态规划都需要保存前一个位置的原值,避免对当前位置的值产生影响。
class Solution {
public int numDistinct(String s, String t) {
int[] dp = new int[s.length() + 1];
Arrays.fill(dp, 1);
int pre = 1;
for(int i = 0; i < t.length(); i ++) {
for(int j = 0; j <= s.length(); j ++) {
int old = dp[j];
if(j == 0) {
dp[j] = 0;
} else if(t.charAt(i) == s.charAt(j - 1)) {
dp[j] = dp[j - 1] + pre;
} else {
dp[j] = dp[j - 1];
}
pre = old;
}
}
return dp[s.length()];
}
}
结果
优化代码二:列主序 + 倒序
换一种方向:对于每个 s 字符串内的字符,都进行更新一次列的值。
仔细观察原来二维 dp 数组的值
- dp[i - 1][j - 1] 等价于列主序的 dp[j - 1]
- dp[i][j - 1] 等价于列主序的 dp[j] 原值
所以在列主序的状态转移方程就变成:
- s[i] == t[j] 时 :dp[j] = dp[j] + dp[j - 1]
- s[i] != t[j] 时 :dp[j] = dp[j]
因而使用列主序的方式可以简化很多代码。
然而此时如果按正序遍历的话当前修改仍然会影响后一个位置,可以使用倒序遍历解决。
class Solution {
public int numDistinct(String s, String t) {
int[] dp = new int[t.length() + 1];
dp[0] = 1;
for(int i = 0; i < s.length(); i ++) {
for(int j = t.length(); j > 0 ; j --) {
if(t.charAt(j - 1) == s.charAt(i)) {
dp[j] += dp[j - 1];
}
}
}
return dp[t.length()];
}
}
结果
最终的优化代码:列主序 + 倒序 + 哈希
从上述优化二可以看出,如果 s 字符串的第 i 个字符与 t 字符串的第 j 个字符不相等,那么原来的值就不会改变。
既然这样,能不能只找 t 字符串中与 s 字符串的第 i 个字符相同的位置呢?
答:可以使用 hash 数组解决。
主要变量解释如下:
-
map[c] :表明此字符在 t 字符串当前索引位置 i 之前最后一次出现的索引位置。
-
next[i] :表明与 t 字符串索引位置 i 的字符相同且在此位置之前最后一次出现的位置。
class Solution {
public int numDistinct(String s, String t) {
int[] dp = new int[t.length() + 1];
dp[0] = 1;
int[] map = new int[128];
Arrays.fill(map, -1);
int[] nexts = new int[t.length()];
for(int i = 0 ; i < t.length(); i ++){
int c = t.charAt(i);
nexts[i] = map[c];
map[c] = i;
}
for (int i = 0; i < s.length(); i ++){
char c = s.charAt(i);
for(int j = map[c]; j >= 0; j = nexts[j]){
dp[j + 1] += dp[j];
}
}
return dp[t.length()];
}
}