大话数据结构之二叉树遍历（详解版，含代码实现）

[开场白]：同学们，大家好！今天这节课我们来探讨一下二叉树的遍历。

  封老师：在正式上课前，我想跟大家玩个小游戏。假如，我手上有5张100元、10张50元还有500张1元的，同时洒向天空，看大家谁最终抢的多。如果是你，你会怎么去抢这些钱呢？

  同学A： 这还不简单呀，肯定是先挑大的捡呗！

  封老师：不错，相信在场的我们都会选择这么做。那么在刚才那个例子中，我们想要在有限时间内，捡到最多的钱，捡钱的次序就显得尤为重要了。同样，对于二叉树的遍历，次序也很重要。接下来，就正式进入了我们今天的课堂内容——二叉树遍历。

[Part 1]：二叉树遍历原理

  封老师：通过刚才的例子，相信大家已经认识到次序的重要性了，那让我们一起来看看二叉树遍历的定义吧。

     Def:二叉树的遍历是指从根节点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问依次且仅被访问一次。

     在这里出现了两个关键词：访问和次序。

     访问其实是根据具体需求来完成某一件事情。在二叉树遍历中，我们可以简单的认为就是输出结点的信息。

     次序就像在我们人生道路上，走完某一阶段，步入另外一个阶段后，由于我们选择的不同，导致我们经历的下一个阶段的不同。在二叉树遍历中，我们可以简单的认为就是遍历完上一个结点后，根据我们遍历方式的不同，遍历的接下来的结点不同。

[Part 2]：二叉树遍历方法

  封老师：根据刚才的思路，我们知道二叉树遍历方法的不同，将会导致遍历次序的不同，那么二叉树的遍历方法又有哪些呢？

      其实，根据二叉树的结构，我们可以知道，它不同于简单的线性结构，在遍历次序上它有很多种选择，我们限制从左到右的习惯方式，那么主要可以分为以下四种：

  1.前序遍历
    规则是若二叉树为空，则空操作返回，否则先访问根节点，然后前序遍历左子树，再前序遍历右子树。 如下图所示：

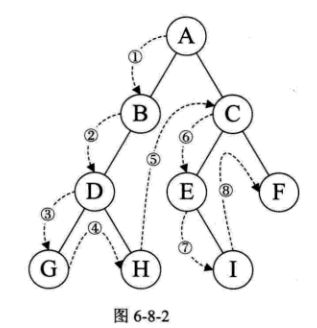
    遍历顺序是：ABDGHCEIF
    代码如下：

/*二叉树的前序遍历递归算法*/
void  PreOrderTraverse(BiTree T)
{
	if(T==NULL)  //二叉树为空 
	  return ;
	printf("%c",T->data); //显示结点数据，可修改为对结点的其它操作 
	PreOrderTraverse(T->lchild); //先序遍历左子树 
	PreOrderTraverse(T->rchild); //先序遍历右子树 
} 

  2.中序遍历
    规则是若二叉树为空，则空操作返回，否则从根节点开始（并不是先访问根节点），中序遍历根节点的左子树，然后访问根节点，最后中序遍历右子树。 如下图所示：

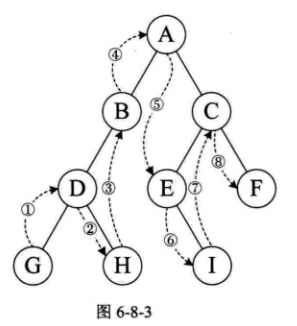
    遍历顺序是：GDHBAEICF
    代码如下：

/*二叉树的中序遍历递归算法*/
void  InOrderTraverse(BiTree T)
{
	if(T==NULL)  //二叉树为空 
	  return ;
	InOrderTraverse(T->lchild); //中序遍历左子树 
	printf("%c",T->data); //显示结点数据，可修改为对结点的其它操作 
	InOrderTraverse(T->rchild); //中序遍历右子树 
} 

  3.后序遍历
    规则是若二叉树为空，则空操作返回，否则从左到右先叶子结后结点的方式遍历访问左右子树，最后是访问根节点。 如下图所示：

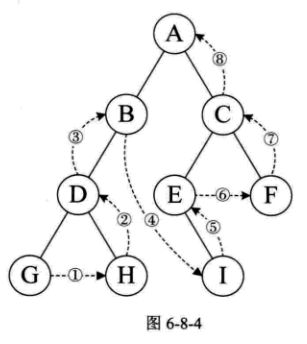
    遍历顺序是：GHDBIEFCA
    代码如下：

/*二叉树的后序遍历递归算法*/
void  PoOrderTraverse(BiTree T)
{
	if(T==NULL)  //二叉树为空 
	  return ;
	PoOrderTraverse(T->lchild); //后序遍历左子树 
	PoOrderTraverse(T->rchild); //后序遍历右子树 
	printf("%c",T->data); //显示结点数据，可修改为对结点的其它操作 
} 

  4.层序遍历
    规则是若二叉树为空，则空操作返回，否则从树的第一层，也就是根节点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。 如下图所示：

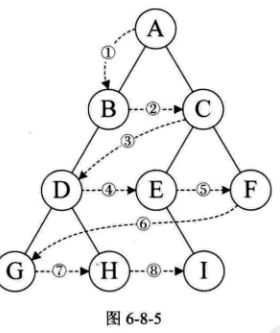
    遍历顺序是：ABCDEFGHI
    代码如下：

/*二叉树的层序遍历算法*/
//采用队列的方式进行实现，参考自Monster_ii博主代码
void LevelOrder(TreeNode *root)
{
    std::queue<TreeNode *> q;
    TreeNode *front;

    if (root == NULL)
	   return;

    q.push(root);

    while (!q.empty())
    {
        front = q.front();
        q.pop();

        if (front->left)
            q.push(front->left);

        if (front->right)
            q.push(front->right);

        printf("%c ", front->data);
    }
}

  封老师：看完这四种遍历的方法，大家有什么想问的吗？

  同学B：封老师，为什么在实现前面三种遍历的时候，采用递归的方式，而在层序遍历的时候却不使用递归的方式了呀？

  封老师：采用递归的方式是因为树的定义本身就是一种递归定义，所以前三种遍历方式（深度遍历）采用递归可以使代码简洁易懂，而对于层序遍历（广度遍历），它需要别的数据结构的支撑，因此我们不采用递归的方式来实现。

[Part 3]：遍历结果的推导

  封老师：同学们，是不是还对刚才的前三种遍历有些疑惑？没关系，接下来的内容可能使你对上面递归的方式有更进一步的认识。

      在二叉树遍历中，有这么一个题目，已知一颗二叉树的前序遍历序列为ABCDEF，中序遍历序列为CBAEDF，请问这颗二叉树的后序遍历结果是什么？谁能解答下这个题吗？

      (底下沉默了几分钟)

  封老师：那大家认真听我接下来的推导过程！

      题目中，给定我们前序遍历的顺序是ABCDEF，我们知道，前序遍历是从根结点开始，先打印再递归左和右。 所以，我们很容易就知道ABCDEF中第一个打印出来的A就是根结点数据。

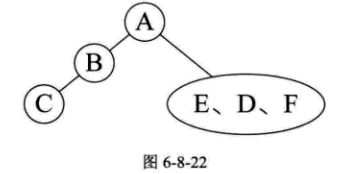
      同样，给定我们中序遍历的顺序是CBAEDF，我们知道，中序遍历也是从根结点开始，不过它先递归左，打印后再递归右。 所以，在根结点A之前的就一定是左子树结点，根结点A之后的就一定是右子树结点。如下图所示：

      对于其它的点，我们也可以采用同样的方法进行判断，过程图如下：

  封老师：在这里有两点二叉树遍历的性质，大家记下笔记：
      1.已知前序遍历和中序遍历序列，可以唯一确定一棵二叉树
      2.已知后序遍历和中序遍历序列，可以唯一确定一棵二叉树

  同学C：老师，已知前序遍历和后序遍历序列呢？

  封老师：emmm,这个问题就留给同学们课后思考吧，大家可以尝试下会出现怎样的情况，下节课我会叫同学上来解释这个问题哦！

[结束语]：今天的课就到这里，下课！