大话数据结构之模式匹配算法（详解版，包含代码实现）

[开场白]：同学们，大家好！今天这节课我们来探讨一下模式匹配算法。

  同学A： 封老师，什么是模式匹配啊？

  封老师：看来这位同学课后预习的不充分呀，待会儿可要认真听讲！不过我相信有很多同学小小的脑袋里也和你一样充满了大大的疑惑。那到底什么是模式匹配呢？老师先给你们讲个通俗的例子把。

      想当年，老师还是学生的时候，有时候需要阅读一些英文的文章或者资料来学习一些知识。但对于只过了四级的英语本渣我来说，只能老老实实的去查英语词典。不过，机智的我发现有很多专业词汇是一样的，所以我就想在那些词汇下面去做中文注释。

      可是实践起来可没有那么简单。在一篇长长的文章寻找那些相同词汇的位置可害惨了我(我推了下我那600度的眼镜)。

      (底下哄笑一堂)

  封老师：安静下，同学们！刚才我所说的寻找单词（子串）在一篇文章（主串）中的定位问题。 而这种子串的定位操作通常称做串的模式匹配。那么我们怎么去解决这个问题呢，这就是我们这节课的重点！

[Part 1]：朴素的模式匹配算法

  封老师：通过刚才的例子，相信大家已经大概了解了什么是模式匹配。那老师出一个小例子，假设我们要从主串S="goodgoogle"中，找到T="google"这个子串的位置。那我们需要哪些步骤呢？以下是我们的通常做法。

     1.从主串S的第一位开始与子串T的字母进行比较，直到匹配失败。很明显在这个例子中，第四个字母处就已经不相同了。这说明从第一位开始匹配失败。如图5-6-1所示：

     2.从主串的第二位开始，重复步骤1的操作。如图5-6-2所示：

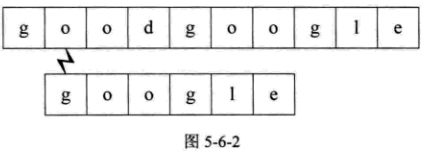
     3.从主串的第三位开始，重复步骤1的操作。如图5-6-3所示：

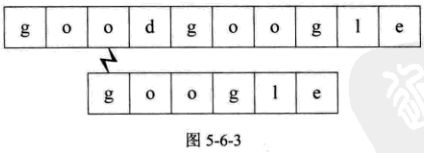
     4.从主串的第四位开始，重复步骤1的操作。如图5-6-4所示：

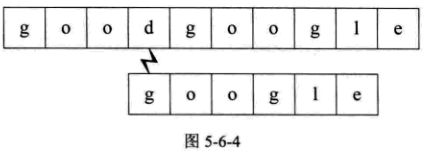
     5.从主串的第五位开始，重复步骤1的操作，这一次终于匹配成功了，太鸡冻了！如图5-6-5所示：

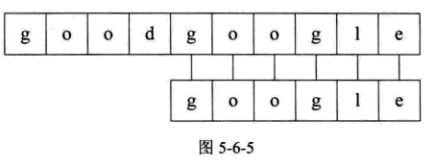
     总的来说，就是将主串的每一个字符作为子串开头进行一次匹配，如果匹配过程中遇到失败（不相等）的情况，则进行下一次匹配，直到匹配成功或全部遍历完。
     接下来我们实现下这个模式匹配的算法。
     Notice:我们假设主串S和子串T的长度均存在S[0]和T[0]中。实现代码如下：

/*返回子串T在主串S中第pos个字符之后的位置。若不存在，则返回0*/
/*其中 T非空，1 <= pos <= StrLength(S) */ 
int Index(String S,String T,int pos)
{
	int i = pos; /*i用于标记主串S当前位置下标*/
				/*从pos位置开始匹配*/ 
	int j = 1; /*j用于标记子串T当前位置下标*/ 
	while(i<=S[0]&&j<=T[0])  
	{
		if(S[i]==T[i]) /*字母相等则继续匹配过程*/ 
		{
			++i;
			++j;
		}
		else    /*字母不相等开始下一个匹配*/ 
		{
			i = i-j+2; /*i为上次开始匹配位置的下一位*/ 
			j = 1;    /*j退回到子串T的首位*/ 
		}
	}
	if(j>T[0]) /*匹配成功*/ 
	{
	 	return i-T[0];
	}
	else
	{
		return 0; /*匹配失败*/ 
	}	 
}

  封老师：关于当前这个实现方法，同学们有什么想法或疑问吗？

  同学B：封老师，我觉得这个算法不够优化，刚才那个例子中，步骤2、3、4是不必要的，因为通过第一轮的匹配，我们已经知道了S[2]、S[3]、S[4]与T[1]不相等，但要想匹配成功，那么子串首字母一定要与主串开始的字母相等，所以步骤2、3、4匹配一定不会成功。

  封老师：同学B的思路不错，希望其他同学也积极思考，踊跃发言。大家掌声鼓励一下！
      (底下响起了一片掌声)

  封老师：同学B从匹配开始的首字母角度出发，使得刚才的算法得到了一定的优化，不过貌似还没有抓住事情的本质。接下来，让我们一起看看我们的前辈们是怎么解决这个问题的！

[Part 2]：KMP模式匹配算法

  封老师：让我们接着刚才的思路，看下面这个问题。

      假设此时的主串S=“abcdefgab”，子串T=“abcdex”，我们怎么对其进行匹配呢？

      同学A，你用我们刚才所学的朴素模式匹配算法在黑板上画下匹配的过程，看看你有没有摸鱼。

      几分钟之后~~

  同学A的答案（朴素模式匹配）：

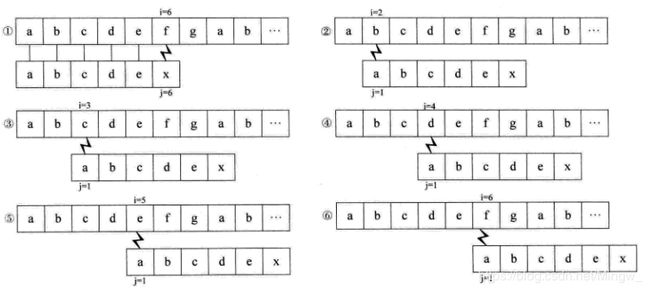
  封老师：emmmm,不错，看来没有在摸鱼！不过根据刚才同学B的想法，我们会发现过程2、过程3、过程4、过程5是不需要的！

  同学C：封老师，按同学B的想法，过程6不应该也是不需要的吗？

     (底下一起附和)对啊，过程6的首字母与子串T的首字母也不相同啊，不应该也不需要了吗？

  封老师：好了，同学们，安静下!让我们回过头来看下刚才的例子中的步骤1：

     刚才同学B说通过步骤1让我们知道T[1]与S[2]、S[3]、S[4]不相等，可是以计算机的角度来看为什么知道它们不相等呢？
     那是因为T[1]与T[4]相等，而与T[2]、T[3]不相等，但T[2]、T[3]却匹配成功，T[4]却匹配失败，因此T[1]与S[2]、S[3]、S[4]一定不相等，而回到我们这个例子的步骤1：

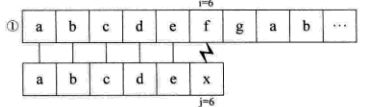
      T[6]与S[6]匹配失败，而且T[6]与T[1]不相等，虽然我们现在能直观的知道步骤6一定是匹配失败的，但是对于计算机来讲，它在那个时刻是没法知道T[1]与S[6]是否相等的。

  封老师：好了，通过刚才的比较大家有没有什么新的发现或想法呢？

  同学B：封老师，我觉得匹配过程的优化可能与子串中是否有相同的字符有关系。
  封老师：嗯，非常棒的想法！那其中到底有怎样的关系呢？这种关系如何运用到我们的算法里面呢？让我们带着这两个想法接着探索新的内容。

      刚才我们已经看过一个子串字符均不相等的例子了，那接下来让我们再看一个子串中含有相等字符的例子，看看能带给我们哪些不一样的思考。

      假设此时的主串S=“abcabcabc”，子串T=“abcabx”，我们又怎样对其进行匹配呢？首先让我们看下它的朴素模式匹配算法下的步骤：

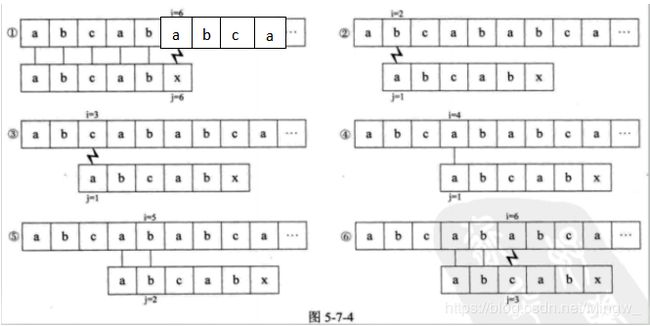
  封老师：那上面的哪些步骤是可以省略的呢？给大家几分钟的思考时间，待会儿，我会叫人起来回答这个问题。

      几分钟之后~~

  封老师：课代表，总是要以身作则的嘛，你来回答下这个问题。

  课代表：封老师，我现在有两个观点：
      1、如果按照刚才根据首字母判断是否需要匹配的话，那么过程2、过程3可以省去。
      2、如果按照所给的过程图来说，我认为过程4、过程5也可以省略，因为在过程1中我们已经知道了T[4]与S[4]、T[5]与S[5]是匹配成功的，那么再去做同样的匹配就显得有些浪费时间了。

  封老师：嗯，回答的不错！很明显第二种观点相对于第一种观点又优化了不少，那到底能不能实现呢？老师先卖个关子，我们来投下票。

      【Y】:可以 【N】:不可以

  封老师：我们先假设刚才观点二是可以实现的，那么此时只剩下了步骤1和步骤6：

  封老师：我们可以很直观的分析出，省略步骤2、3、4、5之后，每次主串开始匹配的首字符一定是上次未匹配成功的，即i值是不会回溯的（i值不会变小），而这也是前辈们所提出的KMP模式匹配算法的核心——让没必要的回溯不发生。所以很显然刚才的答案是“可以”，你做对了吗？不过，KMP模式匹配算法怎样去实现呢？

      通过刚才的分析，我们已经知道了主串S的i值是不会回溯的，那么此时我们需要考虑的就是j值的变化。不妨将T串每个位置j值的变化定义为一个数组next，则问题转换为如何得到next数组。

      首先，我们来看下next数组的函数定义：

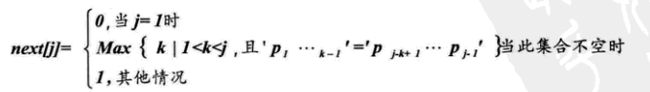
      是不是很多同学都懵圈了？没关系，让我们从实例中来学会如何推导next数组：

      例1：T=“abcdex”

       1）当j=1时，j 到 j-1是没有字符的，因此next[1]=0;
       2）当j=2时，j 到 j-1只有字符“a”，但并未含有字符相等的情况，因此next[2]=1，即在j=2时匹配失败的话，下一步跳转到j=1，进行下一轮匹配；
       3）当j=3时，j 到 j-1有字符串“ab”，但“a”与“b”字符也不相等，因此next[3]=1；
       4）同理，next[4]=1，next[5]=1，next[6]=1，最终可得此时子串T的next[j]为011111；


      例2：T=“abcabx”

       1）当j=1时，next[1]=0;
       2）当j=2时，next[2]=1；
       3）当j=3时，next[3]=1；
       4）当j=4时，next[4]=1;
       5）当j=5时，j 到 j-1有字符串“abca”，因为此时已经匹配到j=5，因此说明前面四步都是匹配成功的，则有:
      S[1]=‘a’=T[1] S[2]=‘b’=T[2] S[3]=‘c’=T[3] S[4]=‘a’=T[4]
      因为T[1]与T[4]相等，因此在下一轮匹配时不需要进行回溯，即当j=5匹配失败时，由于S[4]与T[1]已经相等，因此并不需要i值回溯到4再与T串从头开始进行比较，而只需要从T[2]字符开始与当前的S[i]进行比较。我们可以得到此时next[5]=2；
       6）当j=6时，next[6]=3，理由同上。

      规律：如果T串中前后缀一个字符相等，k值为2；两个字符相等，k值为3；n个k值相等则k值为n+1。


      例3：好了，同学们你们自己动手尝试下这个例子：T=“aaaaax”

      算出来的next[j]=012345，你做对了吗？

      说了这么多，那到底怎样实现KMP模式匹配算法呢？具体代码如下：

/*返回子串T的next数组*/ 
void get_next(String T,int *next)
{
	int i = 1;
	int j = 0;
	next[1] = 0;
	while(i<T[0])
	{
		if(j==0||T[i]==T[j]) /*T[i]表示后缀的单个字符
							 T[j]表示前缀的单个字符*/					 
		{
			++i;
			++j;
			next[i] = j; 
		}
		else
		{
			j = next[j]; /*如果字符不相等，则j回溯*/
		}
	}
} 

/*返回子串T在主串S中第pos个字符之后的位置。若不存在则返回0*/
/*T非空，1<=pos<=StrLength(S)*/ 
int Index_KMP(String S,String T,int pos) 
{
	int i = pos; /*i用于指示主串S当前位置*/
				/*从pos位置开始匹配*/ 
	int j = 1; /*j用于指示子串T当前位置*/ 
	int next[255]; //定义next数组
	get_next(T,next); /*获取子串T的next数组*/
	while(i<=S[0]&&j<=T[0])
	{
		if(j==0||S[i]==S[j])
		{
			++i;
			++j;
		}
		else
		{
			j = next[j]; 
		}
	} 
	if(j>T[0]) //匹配成功 
		return i-T[0];
	else
		return 0; 
}

[Part 3]：KMP模式匹配算法改进

  封老师：同学们，你们觉得这样做是不是最优的呢？

  调皮鬼A：老师你都这么说了，肯定不是最优的。

  封老师：哈哈，不过你能告诉我为什么这样不是最优的吗？或者你能举出一个例子来说明它不是最优的吗？

      (底下沉默了几分钟)

  封老师：同学们，还记得我刚才让你们做的那个例三（T=“aaaaax”）吗？如果这时候它的主串是S=“aaaabcdef”，采用KMP模式匹配算法，这时候它的过程是怎样的呢？如下图所示：

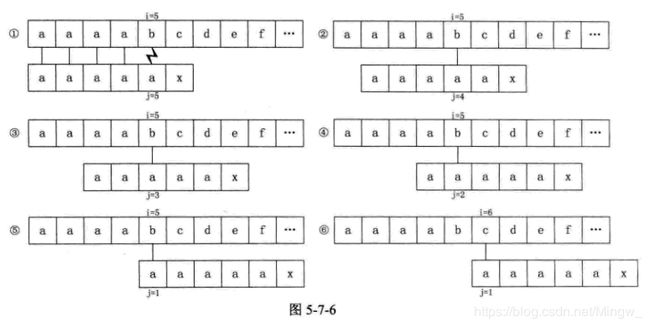
  封老师：不难发现这个过程是不够优化的，可为什么会造成这个现象呢？调皮鬼A你来回答下。

  调皮鬼A：老师，老师我知道了，因为子串T的前面几个字母都是相同的，所以后面步骤2、3、4、5都是不必要的了。

  封老师：emmm，虽然表达的有些口语化，但其中有些本质你还是弄明白了的，那出现这种情况的本质是什么？我们又如何去优化呢？不妨让我们先回到子串T的next数组：
       子串T=“aaaaax”  next[j]=012345

       在next数组中，我们关注的是子串T中前后缀的相似度，但却忽略了本例中next[1]可以取代与它相等的字符后续next[j]的值，因此需要对刚才的next数组改良。下面，我将举两个改良的例子来帮助大家理解。

      例1：T=“ababaaaba”

       1）当j=1时，next数组与改良的nextval数组相等，即nextval[1]=next[1]=0;
       2）当j=2时，第二位字符“b”的next值是1，而第一位字符是“a”，它们不相等，因此nextval[2]=next[2]=1；
       3）当j=3时，第三位字符“a”的next值是1，与第一位字符“a”相等，所以此时nextval[3]=nextval[1]=0；
      通俗的来讲，就是当在j=3这个位置，我们需要回溯的话（即子串j=3位置的字符与主串i位置的字符不匹配），那么按之前的next数组会回溯到j=1的位置，因为j=1与j=3位置的字符相等，所以还是不会匹配，需要继续进行j=1位置的回溯，即回溯到0。
      而nextval数组则去掉了中间环节，即在j=3的位置如果不匹配的话，不会先回溯到1再回溯到0，而是在j=3的位置直接回溯到0。
       4）当j=4时，第四位字符“b”的next值是2，与第二位字符“b”相等，所以此时nextval[4]=nextval[2]=1；
       5）当j=5时，第五位字符“a”的next值是3，与第三位字符“a”相等，所以此时nextval[5]=nextval[3]=0；
       6）当j=6时，第六位字符“b”的next值是4，而第四位字符是“b”，它们不相等，因此nextval[6]=next[6]=4；
       7）当j=7时，第七位字符“a”的next值是2，而第二位字符是“b”，它们不相等，因此nextval[7]=next[7]=2；
       8）当j=8时，第八位字符“b”的next值是2，与第二位字符“b”相等，所以此时nextval[8]=nextval[2]=1；
       9）当j=9时，第九位字符“a”的next值是3，与第三位字符“a”相等，所以此时nextval[9]=nextval[3]=0；


      例2：好了，同学们你们自己动手尝试下这个简单的例子：T=“aaaaaaaab”

      算出来的nextval[j]=000000008，你做对了吗？


  封老师：如果听懂了原理的话，大家是不是觉得改进的nextval数组很容易实现呀，因为我们只要加上判断当前字符与它的前缀字符是否相等就可以了。nextval数组具体代码实现如下：

/*改进的nextval数组*/
void get_nextval(String T,int *nextval)
{
	int i = 1;
	int j = 0;
	nextval[1] = 0;
	while(i<T[0])
	{
		if(j==0||T[i]==T[j]) /*T[i]表示后缀的单个字符
							 T[j]表示前缀的单个字符*/					 
		{
			++i;
			++j;
			if(T[i]!=T[j])  /*当前字符与前缀字符不相等*/
			{
				nextval[i] = j;
			}
			else
			{
				nextval[i] = nextval[j]; /*当前字符与前缀字符相等*/
			}
		}
		else
		{
			j = next[j]; /*如果字符不相等，则j回溯*/
		}
	}
} 

[结束语]：哎，讲了这么多，怎么还有同学没在认真听讲呢？罢了，下课吧！