Leetcode 第191场周赛题解

5424. 数组中两元素的最大乘积

知识点	时间复杂度
暴力枚举	O(n)

从 1 到 n-1 枚举，计算 (nums[i]-1)*(nums[i-1]-1) 。并记录最大值。

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int anw = 0;
        for(int i = 0; i < nums.size(); i++) {
            for(int j = i+1; j < nums.size(); j++) {
                anw = max(anw, (nums[i]-1)*(nums[j]-1));
            }
        }
        return anw;
    }
};

5425. 切割后面积最大的蛋糕

知识点	时间复杂度
排序，枚举	O(nlog(n)+mlog(m))

如果知道切完后蛋糕的最大高度及宽度，那么就可以求得最大面积。

那么如何求得最大高度及长度呢？先以最大宽度为例：

• 向 horizontalCuts 中加入 0, w。
• 将 horizontalCuts 排序。
• 从 1 到 horizontalCuts.size() 枚举 i，记录 horizontalCuts[i] 与 horizontalCuts[i-1] 的最大差值。

最大高度的求解方法类似，不再赘述。

class Solution {
public:
    int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
        sort(horizontalCuts.begin(), horizontalCuts.end());
        sort(verticalCuts.begin(), verticalCuts.end());
        int maxH = max(horizontalCuts[0], h - horizontalCuts[horizontalCuts.size()-1]);
        int maxW = max(verticalCuts[0], w - verticalCuts[verticalCuts.size()-1]);
        
        for(int i = 1; i < horizontalCuts.size(); i++) {
            maxH = max(horizontalCuts[i]-horizontalCuts[i-1], maxH);
        }
        for(int i = 1; i < verticalCuts.size(); i++) {
            maxW = max(verticalCuts[i]-verticalCuts[i-1], maxW);
        }
        return int64_t(maxH)*int64_t(maxW)%1000000007;
    }
};

5426. 重新规划路线

知识点	时间复杂度
邻接表，树的深度遍历	O(Nodes + Edges)

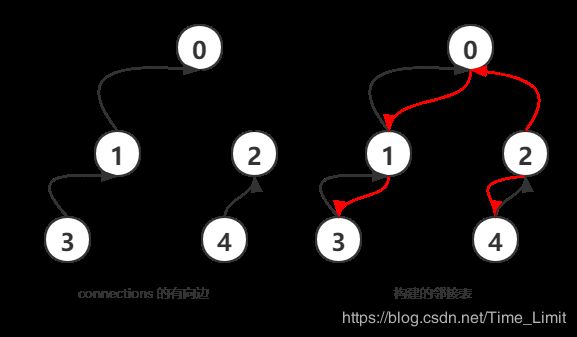
先根据 connections 构建邻接表，以便进行DFS。
构建邻接表时需注意：connections 是有向边，邻接表需构建成无向边。这时我们需要在邻接表中每条边与connections中对应边的方向是否一致。
然后从 0 结点开始遍历，记录遍历过程中，与遍历方向一致的边的数量。
为什么是与遍历方向一致的边呢？因为0 是遍历的起点，而题目描述中， 0 应该是终点。所以与遍历方向一致的边应该被调整。
比如在下图中，遍历过程中用到的邻接表中的边有：

• 0 到 1 的边
• 0 到 2 的边
• 1 到 3 的边
• 2 到 4 的边

其中仅有0到2这一条边，其对应的connections中的边与遍历方向一致。所以需调整的边数为 1 。

class Solution {
public:
    int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
        sort(horizontalCuts.begin(), horizontalCuts.end());
        sort(verticalCuts.begin(), verticalCuts.end());
        int maxH = max(horizontalCuts[0], h - horizontalCuts[horizontalCuts.size()-1]);
        int maxW = max(verticalCuts[0], w - verticalCuts[verticalCuts.size()-1]);
        
        for(int i = 1; i < horizontalCuts.size(); i++) {
            maxH = max(horizontalCuts[i]-horizontalCuts[i-1], maxH);
        }
        for(int i = 1; i < verticalCuts.size(); i++) {
            maxW = max(verticalCuts[i]-verticalCuts[i-1], maxW);
        }
        return int64_t(maxH)*int64_t(maxW)%1000000007;
    }
};

5427. 两个盒子中球的颜色数相同的概率

知识点	时间复杂度
动态规划，排列组合	O(n^3*m^3)，n，m分别为球数和颜色的数量

首先需要解决一个排列问题，向 b 个球种插入 q 个相同的球，一共有多少种不同的插入方法。这个可以参考代码中的 cal 函数及其注释。（或许有高级的排列组合公式？可惜我不会啊！只能用DP了。

其次， 需要计算总的排列数 all，及可行的排列数 correct。(还是用DP来解决
设，dp(i,j,k,p,q) 代表放完前 i 种颜色时，前半部分有 j 个球，p 种颜色，后半部分有 k 个球，q 种颜色的方案数。那么：

• 总排列数 all = Σ dp(m, n/2, n/2, i, j)
• 可行的排列数 correct = Σ dp(m，n/2，n/2，i，i)
• 最终的答案为 correct/all

状态转移考虑，对于第 i 种颜色有 t 个球给前半部分，balls[i]-t 给后半部分。那么：

• pcu = t > 0 ? 1 : 0
• scu = balls[i]-t > 0 ? 1 : 0
• dp(i,j,k,p,q) = Σ dp(i-1, j-t, k-balls[i]+t, p-pcu, q-scu)

详细解释可以参见注释。

class Solution {
public:
    long double solution[26][26];
    //solution[i][j] 表示已有i个球，向其中插入j个相同的球的方案数。
    //solution 是通过下面的 dfs 函数计算得出的。

    long double dp[9][25][25][9][9];
    //dp[i][j][k][p][q] 表示排完前i中颜色时，第一堆有 i 个球，p 种颜色，第二堆有 j 个球，q 种颜色的方案数。

    long double cal(int a, int p) {
        return dfs(p+1, a); 
        // 已有 p 个球，那么相当于有 p+1 个槽可以插入 a 个球。
        // 所以cal(a, p) == dfs(p+1, a);
    }

    // 有 slots 个槽，插入 balls 个球的方案数。
    long double dfs(int slots, int balls) {
        if(slots == 0) {
            if(balls != 0) {
                return 0; // 0 个槽，1 个球，显然没得插
            }
            return 1; // 0 个槽，0个球，显然只有一种方案
        }
        if(balls == 0) {
            return 1; //多个槽， 0 个球，显然也只有一种方案。
        }

        //solution 其实是一个记忆化数组。
        //solution 会初始化为 -1。如果其大于 -0.5 说明已被计算过。不和 0 做比较是为了避免精度问题。
        if(solution[slots][balls] > -0.5) {
            return solution[slots][balls];
        }

        long double anw = 0;
        for(int i = 0; i <= balls; i++) {
            // 在当前槽种放入 i 个球。
            anw += dfs(slots-1, balls-i);
        } 
        solution[slots][balls] = anw;
        return anw;
    }
    long double alloc(int a, int b, int p, int q) {
        //前半部分已有 p 个球，需插入 a 个。
        //后半部分已有 q 个球，需插入 b 个。
        return cal(a, p) * cal(b, q);
    }
    double getProbability(vector<int>& balls) {
        // 初始化 solution 数组。
        for(int i = 0; i <= 25; i++) {
            for(int j = 0; j <= 25; j++) {
                solution[i][j] = -1;
            }
        }
        //统计球的个数
        int n = 0;
        for(auto v : balls) {
            n += v;
        }
        memset(dp,0, sizeof(dp));
        dp[0][0][0][0][0] = 1;
        //枚举颜色
        for(int i = 1; i <= balls.size(); i++) {
            int cnt = balls[i-1];
            //枚举当前颜色在前半部分放了 j 个球， 后半部分放了 cnt -j 个球。
            for(int j = 0; j <= cnt; j++) {
                //放完当前颜色之后，前半部分一共有 p 个球。
                for(int p = j; p <= n/2; p++) {
                    //放完当前颜色之后，前半部分一共有 q 个球。
                    for(int q = cnt-j; q <= n/2; q++) {
                        int preDiff = ((j == 0) ? 0 : 1);
                        int sufDiff = (((cnt - j) == 0) ? 0 : 1);
                        // preDiff，sufDiff 分别代表在放完之后，前后两部分是否新增了一种颜色。
                        for(int b = preDiff; b <= i; b++) {
                            for(int d = sufDiff; d <= i; d++) {
                                //b, d 代表放完当前颜色之后，前后两部分的颜色数量。
                                dp[i][p][q][b][d] += dp[i-1][p-j][q-(cnt-j)][b-preDiff][d-sufDiff] * alloc(j, cnt-j, p-j, q-(cnt-j));
                                /*
                                if (dp[i][p][q][b][d]) {
                                    cout << j << " " << cnt-j << " " << preDiff << " " << sufDiff << endl;
                                    cout << p-j << " " << q-(cnt-j) << endl;
                                    cout << alloc(j, cnt-j, p-j, q-(cnt-j)) << endl;
                                    cout << cal(j, p-j) << " " << cal(cnt-j, q-(cnt-j)) << endl;
                                    cout << i << " " << p << " " << q << " " << b << " " << d << " " << dp[i][p][q][b][d] << endl;
                                }
                                */
                            }
                        }
                    }
                }
            }
        }
        long double correct = 0, all = 0;
        for(int i = 0; i <= balls.size(); i++) {
            correct += dp[balls.size()][n/2][n/2][i][i];
        }
        for(int i = 0; i <= balls.size(); i++) {
            for(int j = 0; j <= balls.size(); j++) {
                //cout << i << " " << j << " " << dp[balls.size()][n/2][n/2][i][j] << endl;
                all += dp[balls.size()][n/2][n/2][i][j];
            }
        }
        //cout << correct << " " << all << endl;
        return correct/all;
    }
};