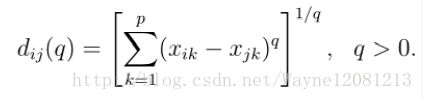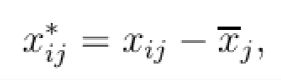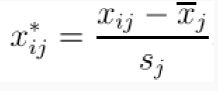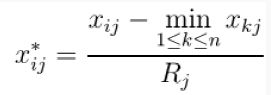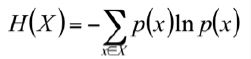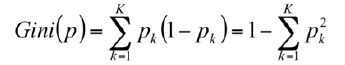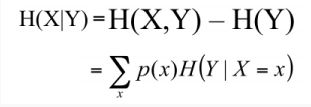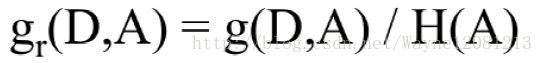机器学习（1）k最近邻算法、朴素贝叶斯算法、聚类算法、

k最近邻算法

1. 原理

• 数据映射到高维空间中的点
• 找出k个最近的样本
• 投票结构

2.如何衡量距离

数学中距离满足三个要求

• 必须为正数
• 必须对称
• 满足三角不等式

3.闵可夫斯基距离（Minkowski）：

• 汉哈顿距离
• 欧氏距离
• 切比雪夫距离

公式：

q越大，差异越大的维度对最终距离影响越大

q = 1时为曼哈顿距离

q = 2时为欧式距离

q无穷大时为切比雪夫距离

4.马氏距离

考虑数据分布

5.KNN分类实现的简单案例

from dataminer.baseClassifier.baseClassifier import BaseClassifier
from dataminer.mltools.stats.distance import Distance
import operator
class KNNClassifier(BaseClassifier):
    def __init__(self,traingfilesname,fieldsrols,delimiter,k=10):
        super(KNNClassifier,self).__init__(traingfilesname,fieldsrols,delimiter)
        self.k=k



    def _findNearestNeighbor(self,item):
        neighbors=[]
        for idx,onerecord in enumerate(self._data['prop']):
            distance=Distance.computeManhattanDistance(onerecord,item)
            neighbors.append([idx,distance,self._data['class'][idx]])

        neighbors.sort(key=lambda x:x[1])

        nearestk={}
        for i in range(self.k):
            nearestk.setdefault(neighbors[i][2],0)
            nearestk[neighbors[i][2]]+=1

        return nearestk

    def predicate(self,item):
        nearestk=self._findNearestNeighbor(item)
        ps=sorted(nearestk.items(),key=lambda x:x[1],reverse=True)
        return ps[0][0]

class Distance(object):
    @staticmethod
    def computeManhattanDistance(vector1,vector2,q=1):

        """

        :param vector1: [1,2,3,45,6]
        :param vector2: [1,2,4,56,7]
        :return:
        """
        distance=0.
        n=len(vector1)
        for i in range(n):
            distance +=pow(abs(vector1[i]-vector2[i]),q)
        return round(pow(distance,1.0/q),5)
    @staticmethod
    def computeEuDistance(vector1,vector2):
        return Distance.computeManhattanDistance(vector1,vector2,2)

朴素贝叶斯算法

1. 概率的基本性质

• 事件的概率在0~1之间，即0<=P(A)<=1
• 必然事件的概率为1
• 不可能事件的概率为0
• 概率的加法公式：P(A并B) = P(A) + P(B)（当事件A与B互斥时）
• 事件B与事件A互为对立事件，P(A并B)=1.由加法公式得到P(A) =  1 - P(B)

2. 概率的基本知识

1）先验概率P(A)

2）后验概率（条件概率）P(A|B)

3）概率乘法公式：P(AB) = P(A) * P(B|A)

P(A|B) = P(A) * P(B|A) / P(B)

3. 全概率公式

P(B) = P(A1B + A2B + ··· + AnB)

4. 贝叶斯定理

P(Ak|B) = P(AkB) / P(B) （k = 1,2,···,n）

5. 应用场景：垃圾邮件过滤、新闻分类、金融风险识别

6. 

1）先验概率：事件A1, A2, ···, An看作是导致事件B发生的“原因”，在不知事件B是否发生的情况下，它们的概率为P(A1), P(A2), ···, P(An)，通常称为先验概率。

2）后验概率：现在有了新的信息已知（B发生），我们对A1, A2, ··· An发生的可能性大小P(A1|B), P(A2|B), ···, P(An|B)有了新的估价，成为“后验概率”。

3）全概率公式看成“由原因推结果”，而贝叶斯公式的作用在于“由结果推原因”：现在一个“结果”A已经发生了，在众多可能的“原因”中，到底是哪一个导致了这一结果。故贝叶斯公式也称为“逆概公式”。

7. 代码案例：

from dataminer.baseClassifier.baseClassifier import BaseClassifier


class NativeBayesianClassifier(BaseClassifier):
    def __init__(self, datafilename, fieldroles, delimiter):
        super(NativeBayesianClassifier, self).__init__(datafilename, fieldroles, delimiter)
        self._postProb = dict()  # 条件概率，后验概率 P(B|A)
        self._priorProb = dict()  # 先验概率 P(A)
        self._classStats=dict()
        self._categroyPropStatsByClass = dict()

        """
        {
            'class1':{
                col1:{
                        value1:10,
                        value2:20,
                        value3:30
                 },
                col2:{
                        value1:10,
                        value2:20,
                        value3:30
                }
            },
            'class2':{
            }
        }
        """

    def _baseStat(self):
        for idx, rcdClass in enumerate(self._data['class']):
            self._categroyPropStatsByClass.setdefault(rcdClass, {})
            self._classStats.setdefault(rcdClass,0)
            self._classStats[rcdClass] +=1
            for fieldIdx, fieldValue in enumerate(self._data['prop'][idx]):
                self._categroyPropStatsByClass[rcdClass].setdefault(fieldIdx, {})
                self._categroyPropStatsByClass[rcdClass][fieldIdx].setdefault(fieldValue, 0)
                self._categroyPropStatsByClass[rcdClass][fieldIdx][fieldValue] += 1


    def _computePriorProbability(self):
        recordsCnt=len(self._data['class'])
        for rcdClass,cnt in self._classStats.items():
            self._priorProb.setdefault(rcdClass,round(cnt*1./recordsCnt,2))


    def _computePostProbablity(self):
        for oneClass,classStats in self._categroyPropStatsByClass.items():
            self._postProb.setdefault(oneClass,{})
            thisClassCnt=self._classStats[oneClass]
            for oneColumn,valueStats in classStats.items():
                self._postProb[oneClass].setdefault(oneColumn,{})
                for oneValue,valueCnt in valueStats.items():
                    self._postProb[oneClass][oneColumn].setdefault(oneValue,round(valueCnt*1./thisClassCnt,3))




    def trainingModel(self):
        self._baseStat()
        self._computePriorProbability()
        self._computePostProbablity()

    def predicate(self,item):
        result=[]
        for oneClass,priorProp in self._priorProb.items():
            prop = priorProp
            for idx,fieldValue in enumerate(item):
                conditionProp = self._postProb[oneClass][idx].get(fieldValue,0)
                if conditionProp != 0:
                    prop = prop * conditionProp
            result.append((oneClass,prop))

        result.sort(key=lambda x:x[1],reverse=True)
        return result

聚类算法

1.聚类和分类的区别

聚类是无监督的学习

分类是有监督的学习

1）聚类的场景：使用聚类不需要提前被告知要划分的组是什么样的，在不知道找什么时就自动完成分组

2）无监督学习算法--聚类算法一览：

层次聚类法、Kmeans、密度聚类法、谱聚类、GMM、LDA

3）基于距离：

层次聚类法、K-means聚类法、K-center聚类发

4）基于密度：

密度距离法（DBCSAN）

2.层次聚类法

• 找到两个最近的两个点（类）；
• 把它们合成一个点（类）；（这个新的点不是数据集中本来存在的点，把原来那两个点删掉，用这个点代替原来两点）
• 重复上面两步，最终得到一棵树

1）类间距离的计算

• 最短距离法
• 最长距离法
• 中间距离法
• 类平均法

不同的距离方法，得到不同的结果（算法不稳定）

3. K-means聚类法

• 随机选择k个点作为初始质心
• 把每个点按照距离分配给最近的质心，形成k个簇
• 重新计算每个簇的质心
• 重复以上两步，直到质心不再变化

4. 数据变换

中心化变换：均值为0，方差不变

标准化变换：均值为0，方差为1

极差正规化变换：极差为1，数值在[0,1]之间

5.代码案例

class KMean(object):
    def __init__(self, k):
        self._data = []
        self._normalizeData = []
        self._memeberOfClusters = []
        self._maxIteration = None

        self._clusterCenters = []
        self._pointChangedNum = 0
        self._k = k
        self._comment = []
        # self._loadIirsDataFile(datafiles)
        # self._normalized()

    def _loadIirsDataFile(self, datafile):
        file = open(datafile)
        for lineIdx, line in enumerate(file):
            columns = line.strip('\n').split(',')[:4]
            floatColumns = map(float, columns)
            self._data.append(floatColumns)
            self._memeberOfClusters.append(lineIdx)
        file.close()

    def loadDataFiles(self, datafilenames, commentId, delimiter=','):
        for oneFile in datafilenames:
            file = open(oneFile)
            lineIdx = 0
            for line in file:
                vector = []
                columns = line.strip('\n').split(delimiter)
                for cid, value in enumerate(columns):
                    if cid == commentId:
                        self._comment.append(value)
                    else:
                        vector.append(float(value))
                self._data.append(vector)
                self._memeberOfClusters.append(lineIdx)
                lineIdx += 1

    def _getColumn(self, colIdx):
        column = [self._data[i][colIdx] for i in range(len(self._data))]
        return column

    def _getColumnMeanAndStd(self, column):
        sumx = 0.0
        sumx2 = 0.0
        for x in column:
            sumx += x
            sumx2 += x ** 2
        n = len(column)
        mean = sumx / n
        d = sumx2 / n - mean ** 2
        std = pow(d, 0.5)

        return (round(mean, 3), round(std, 3))

    def _getColumnMedian(self, column):
        columncopy = list(column)
        columncopy.sort()
        clen = len(columncopy)
        if clen % 2 == 0:
            return (columncopy[clen / 2] + columncopy[clen / 2 - 1]) / 2
        else:
            return columncopy[(clen - 1) / 2]

    def _normalizeOneColumn(self, column):
        cmedian = self._getColumnMedian(column)
        csum = sum([abs(x - cmedian) for x in column]) * 1.0
        asd = round(csum / len(column), 3)

        result = [round((x - cmedian) / asd, 3) for x in column]
        return result

    def normalized(self, normalize=False):
        if not normalize:
            self._normalizeData = self._data
        else:
            cols = len(self._data[0])
            rows = len(self._data)

            self._normalizeData = [[0] * cols for i in range(rows)]

            for i in range(len(self._data[0])):
                oneColumn = self._getColumn(i)
                result = self._normalizeOneColumn(oneColumn)

                for rowidx, value in enumerate(result):
                    self._normalizeData[rowidx][i] = result[rowidx]

    def _initializeCenters(self):
        randLineIdx = random.sample(range(len(self._data)), self._k)
        for lIdx in randLineIdx:
            self._clusterCenters.append(self._normalizeData[lIdx])

    def _selectCloestToCenters(self,point,centers):
        result = Distance.computeEuDistance(point,centers[0])
        for center in centers[1:]:
            distance=Distance.computeEuDistance(point,center)
            if distance < result:
                result=distance
        return result
    def _initailizeCentersByRoulette(self):
        self._clusterCenters=[]
        total=0
        firstCenter=random.choice(range(len(self._data)))
        self._clusterCenters.append(self._normalizeData[firstCenter])

        for i in range(self._k-1):
            weights = [self._selectCloestToCenters(x,self._clusterCenters) for x in self._data]
            total=sum(weights)
            weights = [w/total for w in weights]
            num = random.random()
            total=0.0
            x=-1
            while total

决策树

1. 

决策树：

ID.3、C4.5、C5.0

CART(Classification and Regression Tree, 分类回归树)

元模型：

Bagging、Boosting、随机森林

ID3：信息增益、没有修剪

C4.5：信息增益率、悲观剪枝法

C5.0：信息增益率、自适应增强

CART：基尼指数、“代价复杂度”剪枝法

2. 决策树：

1）对样本数据不断分组过程，是个线性分类器

2）术语

根节点：一棵决策树只有一个根节点

叶节点：代表一个类别

中间节点：代表在一个属性上的测试

分支：代表一个测试输出

3）二叉树和多叉树

二叉树：每个节点最多有两个分支

多叉树：每个节点不止有两个分支

4）树的生长

采用分而治之的策略

选变量的顺序：如何从众多决策变量中选择一个当前最佳的决策变量；

最佳分离点在哪：如何从分组变量的众多取值中找到一个最佳的分割点；

5）树的修剪

避免过度拟合：过于个性化、失去了一般性

6）度量信息混杂程度的指标

熵：

基尼系数：

7）熵的理解

事件X的信息量的期望

事件的X的结果发生的概率越小，信息熵越小

定义一个结果的信息量：h(x) = -logx

所有结果的信息量，或者事件X的信息量的期望

熵是随机变量不确定性的量化指标，越不确定，熵越大

8）条件熵

在知道了条件Y之后，X事件仍然具有的不确定性

9）信息增益（互信息）

在知道了事件Y之后，X事件不确定性减少程度

Gain = 熵 - 条件熵

选择信息增益最大的属性作为决策属性（ID3）

10）信息增益率

信息增益倾向于选择更混杂的属性

信息增益的改进：增益率

C4.5

案例代码：

class DecisionTree(object):
    def __init__(self):
        pass

    def _getDistribution(self,dataArray):
        distribution = defaultdict(float)
        m, n = np.shape(dataArray)
        for line in dataArray:
            distribution[line[-1]] += 1.0/m
        return distribution

    def _entropy(self, dataArray):
        ent = 0.0
        distribution=self._getDistribution(dataArray)
        for key, prob in distribution.items():
            ent -= prob * mt.log(prob, 2)
        return ent

    def _conditionEntropy(self, dataArray, colIdx):
        valueCnt = defaultdict(int)
        m, n = np.shape(dataArray)
        condEnt = 0.0
        uniqueValues = np.unique(dataArray[:, colIdx])
        for oneValue in uniqueValues:
            oneData = dataArray[dataArray[:, colIdx] == oneValue]
            oneEnt = self._entropy(oneData)
            prob = float(np.shape(oneData)[0]) / m
            condEnt += prob * oneEnt
        return condEnt

    def _infoGain(self,dataArray,colIdx,baseEnt):
        condEnt=self._conditionEntropy(dataArray,colIdx)
        return baseEnt-condEnt

    def _chooseBestProp(self,dataArray):
        m,n = np.shape(dataArray)
        bestProp = -1
        bestInfoGain=0
        baseEnt = self._entropy(dataArray)
        for i in range(n-1):
            infoGain=self._infoGain(dataArray,i,baseEnt)
            if infoGain > bestInfoGain:
                bestProp=i
                bestInfoGain=infoGain
        return bestProp

    def _splitData(self,dataArray,colIdx,splitValue):
        m,n=np.shape(dataArray)

        cols=np.array(range(n)) != colIdx
        rows=(dataArray[:,colIdx]==splitValue)

        # data=dataArray[rows,:][:,cols]
        data=dataArray[np.ix_(rows,cols)]
        return data

    def createTree(self,dataArray):

        # 1.选择当前最好的分类属性，并创建当前树的根节点和分支
        """
        {'c3': {
                'aggressive': {
                        'c1': {'appearance': {'c4': {'yes': 'i500', 'no': 'i100'}}, 'health': 'i500', 'both': 'i500'}}, 'moderate': {'c1': {'both': 'i100', 'health': {'c2': {'active': 'i500', 'sedentary': {'c4': {'yes': 'i500', 'no': 'i100'}}}}, 'appearance': {'c4': {'yes': 'i500', 'no': 'i100'}
                        }
                        }
                        }
                }
        }
        """
        m,n=np.shape(dataArray)
        if len(np.unique(dataArray[:,-1])) == 1:
            return (dataArray[0,-1],1.0)
        if n==2:
            distribution=self._getDistribution(dataArray)
            sortProb=sorted(distribution.items(),key=lambda x:x[1],reverse=True)
            return sortProb
        rootNode={}
        bestPropIdx=self._chooseBestProp(dataArray)
        rootNode[bestPropIdx] = {}
        uniqValues=np.unique(dataArray[:,bestPropIdx])
        for oneValue in uniqValues:
            splitDataArray=self._splitData(dataArray,bestPropIdx,oneValue)
            rootNode[bestPropIdx][oneValue]=self.createTree(splitDataArray)
        return rootNode


if __name__ == '__main__':
    from dashengml.loaddata import loadBuyComputerData2 as loadBuyComputerData
    import numpy as np
    data, colnames, classvector = loadBuyComputerData()
    dataarray = np.array(data)
    dt=DecisionTree()
    tree=dt.createTree(dataarray)
    print tree
    import treePlotter as tp
    import matplotlib.pyplot as plt

    tp.createPlot(tree)