FFT详解及C语言实现

FFT详解及C语言实现

DFT是干嘛的？

​ 离散傅里叶变换（DFT），是傅里叶变换在时域和频域上都呈现离散的形式，将时域信号的采样变换为在离散时间傅里叶变换（DTFT）频域的采样。在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应当将其看作经过周期延拓成为周期信号再作变换。在实际应用中通常采用快速傅里叶变换以高效计算DFT。 ——百度

FFT是干嘛的？

​ 快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。——百度

​ 在这里我的理解就是：DFT将离散的时域信号转化为离散的频域信号，而FFT就是在计算机上加速计算这一过程的算法的统称。

直接计算DFT

首先我们看一下DFT变换对的公式

正变换：
$$X（k）=DFT[x(n)]=\sum _{n=0}^{N-1}x(n)W_N^{nk}$$
反变换：
$$x(n)=IDFT[X(k)]=\frac{1}{N}\sum _{k=0}^{N-1}X(k)W_N^{-nk}$$
​ 可以很明显的看出反变换相对于正变换来说只是符号不一样以及多了一个比例因子，因为DFT和IDFT的计算量及其的相似，所以只需以正变换为例来考虑直接计算DFT时所存在的问题。

​ 如果直接的计算DFT，要计算离散频谱X(k)的某一个值需要进行N次复数乘法与N-1次复数加法运算，因为一共需要计算N个复数的值，所以总共要计算N×N次复数乘法和N×（N-1）次复数加法，当N的值非常大的时候N×（N-1）约等于N×N，因此1D的DFT原始算法的时间复杂度是 O(n2) ，对于2D的DFT其时间复杂度是 O（n4)…这个计算量是非常恐怖的。

举个例子：计算序列{2，3，3，2}的DFT变换。
$$X[0]=2W_4^0+3W_4^0+3W_4^0+2W_4^0=10$$

$$X[1]=2W_4^0+3W_4^1+3W_4^2+2W_4^3=-1-i$$

$$X[2]=2W_4^0+3W_4^2+3W_4^4+2W_4^6=0$$

$$X[3]=2W_4^0+3W_4^3+3W_4^6+2W_4^9=-1+i$$

​ 可以看出计算一个长度为4的序列的DFT需要计算乘法16次，加法12次，当序列的长度非常大的时候计算量就非常大了，为了加快这一过程，于是就产生了FFT。

FFT算法理解

​ 首先我们来看一下下面这个多项式，
$$f(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+....+a_n{x}^n$$
​ 如果单纯的直接计算，那么时间复杂度为 O(n2)，那么应该如何简化这一个过程呢？这也可能就是傅里叶的无敌之处。

傅里叶说：
$$x=W_N^k$$
可以简化这个过程。

然后你会发现把上式带入多项式中就得到了我们熟悉的这个东西。
$$f(W_N^k)=a_0+a_1{W}_N^k+a_2{W}_N^{2k}+.....+a_n{W}_N^{kn}$$
是不是很阳朔，其实他就是DFT的公式。
$$X（k）=DFT[x(n)]=\sum _{n=0}^{N-1}x(n)W_N^{nk}$$
再来讲一下下面这个东西究竟为何物
$$W_N^k$$
在讲之前补习一下复数的知识。

复数

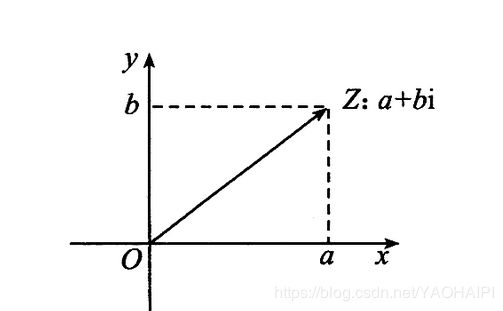
我们把形如z=a+bi（a,b均为实数）的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。当z的虚部等于零时，常称z为实数；当z的虚部不等于零时，实部等于零时，常称z为纯虚数。复数域是实数域的代数闭包，即任何复系数多项式在复数域中总有根。 复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。——百度

1、坐标轴表示

x轴表示的是复数的实部a，y轴表示的是复数的虚部分b,他们的模长可以表示为：
$$|Z|=\sqrt{a^2+b^2}$$

2、复数的运算

设两个复数分别为Z1=a+bi，Z2=c+bi

$$Z_1+Z_2=(a+c)+(b+d)i$$

$$Z_1{Z}_2=(ac-bd)+(ad+bc)i$$

乘法的极坐标表示为
$$(a_1,{\theta }_1)\ast (a_2,{\theta }_2)=(a_1{a}_2,{\theta }_1+{\theta }_2)$$
可以看出复数相乘的实质就是：模长相乘，极角相加。（这个性质很重要）

旋转因子的引入

​ 因为在计算多项式的时候，如果暴力计算，
$$f(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+....+a_n{x}^n$$
​ x的n次方会非常的难算，这该如何是好呢？
$$x_0,x_0^2,x_0^3......x_0^n$$
​ 我们可以引入一些特别的x，让他们的若干次平方之后结果为1

​ 首先我们可以想到1和-1满足条件，1的多少次方都是1，-1的偶数次方是1，但是又出现了一个新的问题，那就是1和-1只有两个数，而多项式需要的是n个不同的数。

​ 然后我们想到了复数，1，i，-1，-i，但是这也只有4个数，依然无法满足条件。

​ 最后傅里叶引入了一个单位圆

这个图网上盗来的，它把圆分成了8等份，对应着时域信号的8个离散数据和频域的8个采样点

然后把圆N等分（N是2的整数次幂）就得到了
$$W_N^k$$
其中k就是圆的第k等份

由旋转因子的对称性、均匀性、周期性，我们可以整理出旋转因子的两个很重要的性质，
$$W_N^k=W_{2N}^{2k}$$

$$W_N^{k+\frac{\pi }{2}}=-W_N^k$$

注意：这两个性质很重要

带入旋转因子进行计算

将
$$x=W_N^k$$
带入多项式，变换成如下形式：
$$C_k=A_0+A_1(W_N^k)+A_2(W_N^k{)}^2+A_3(W_N^k{)}^3+......+A_n(W_{N-1}^k{)}^{n-1}$$
将寄数项和偶数项分离：
$$C_k=(A_0+A_2(W_N^k{)}^2+A_4(W_N^k{)}^4+.....+A_{N-2}(W_N^k{)}^{N-2}+W_N^k(A_1+A_3(W_N^k{)}^2+A_5(W_N^k{)}^4+.....A_{n-1}(W_N^k{)}^{n-2})$$
然后
$$(W_N^k{)}^2=W_N^{2k}=W_{\frac{N}{2}}^k$$
剑上述结果带入
$$C_k=(A_0+A_2{W}_{\frac{N}{2}}^k+A_4(W_{\frac{N}{2}}^k{)}^2+....+A_{n-2}(W_{\frac{N}{2}}^k{)}^{\frac{N}{2}-1})+W_N^k(A_1+A_3{W}_{\frac{N}{2}}^k+A_5(W_{\frac{N}{2}}^k{)}^2+......A_{n-1}(W_{\frac{N}{2}}^k{)}^{\frac{N}{2}-1})$$
此时你会惊讶的发现：左边Ak
$$A_k=A_0+A_2{W}_{\frac{N}{2}}^k+A_4(W_{\frac{N}{2}}^k{)}^2+.....+A_{n-2}(W_{\frac{N}{2}}^k{)}^{\frac{N}{2}-1}$$
就是多项式
$$A_0+A_{2}x+A_4{x}^2+.....+A_{n-2}{x}^{\frac{N}{2}-1}$$
带入了
$$x=W_{\frac{N}{2}}^k$$
的结果。

右边Bk
$$B_k=A_1+A_3{W}_{\frac{N}{2}}^k+A_5(W_{\frac{N}{2}}^k{)}^2+......A_{n-1}(W_{\frac{N}{2}}^k{)}^{\frac{N}{2}-1}$$
就是多项式
$$A_1+A_{3}x+A_5{x}^2+.....+A_{n-1}{x}^{\frac{N}{2}-1}$$
带入了
$$x=W_{\frac{N}{2}}^k$$
的结果。

此时这两个多项式恰好有都有N/2项，

把n个n次复根带入一个长度为n的多项式，是我们要做的DFT过程，那把n/2个 n/2次复根带入一个长度为n/2的多项式，是不是也可以看成是DFT？

依此类推：我们可以得到
$$C_k=A_k+W_N^k{B}_k$$
但是此时0<= k <=N/2的，那另一半如何表示呢？

根据
$$W_N^{k+\frac{\pi }{2}}=-W_N^k$$
在
$$C_k=(A_0+A_2(W_N^k{)}^2+A_4(W_N^k{)}^4+.....+A_{N-2}(W_N^k{)}^{N-2}+W_N^k(A_1+A_3(W_N^k{)}^2+A_5(W_N^k{)}^4+.....A_{n-1}(W_N^k{)}^{n-2})$$
这个式子中，除了奇数次项提出的一个
$$W_N^k$$
是奇数次幂，其他的都是偶数次幂，因此可以表示为：
$$C_{k+\frac{\pi }{2}}=A_k-W_N^k{B}_k$$
此时0<= k <=N/2。

继续递归即可，把一个长度为N/2的多项式分成两个长度为N/4的多项式，然后DFT递归直到到多项式长度为1为止（因为长度为1的多项式只有常数项，变换结果就是其本身）。

以一个8点的离散数据点为例

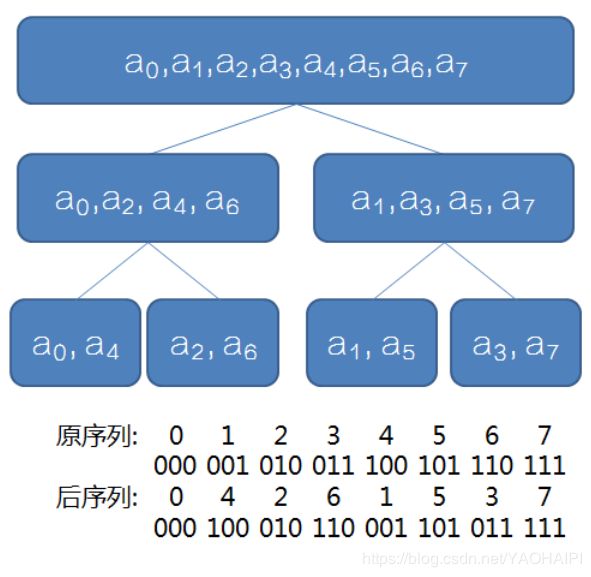
可以发现通过一次又一次的分割，最后把8点数据分成8个独立的点，

它们分割后排序的二进制表示刚好就是没分割前的二进制表示的相反结果

FFT蝶形的运算

其实上面说了那么多，就是为了搞出来这两个东西
$$C_k=A_k+W_N^k{B}_k$$

$$C_{k+\frac{\pi }{2}}=A_k-W_N^k{B}_k$$

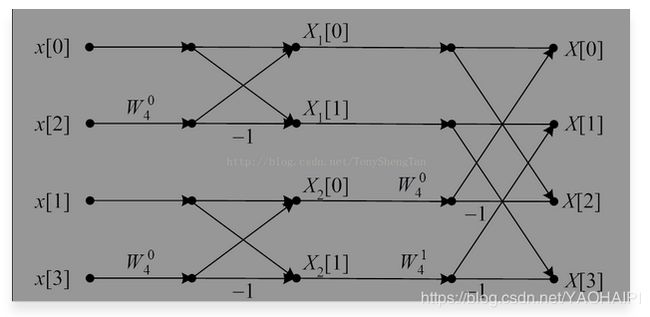
首先以一个4点数据为例（开始疯狂盗图）

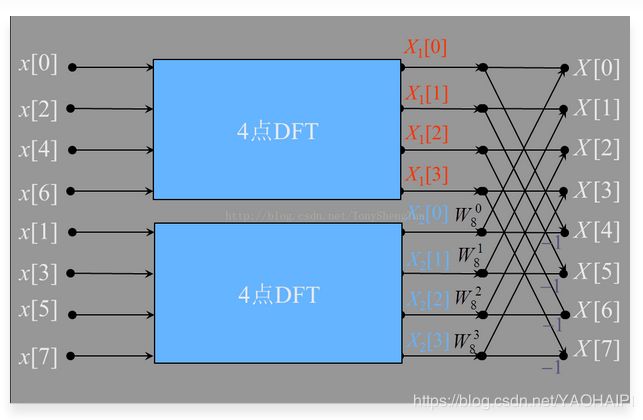
然后再来一个8点的

计算过程

计算结果

C程序实现

1、定义复数的输出函数

​ 已知复数是a+bi的形式，在程序中，为了方便计算，将复数的实部和虚部分离开来进行计算，最后在输出的时候在进行合并。

void output()
{
	int i;
	for(i=0;i<size;i++)
	{	
		printf("%.4f",x[i].real); //输出复数的实部
		if(x[i].imag>=0.0001)
		{
			printf("+%.4fj\n",x[i].imag);  //当复数的虚补大于0.0001时，输出+ 虚部 j的形式
		}
		else if(fabs(x[i].imag)<0.0001)
		{
			printf("\n");//当虚部小于0.001时，跳过虚部，不输出
		}
		else
		{
			printf("%.4fj\n",x[i].imag);//上述两个条件除外的形式，输出 虚部 j的形式
		}
	}
}

2、数据点经过log(N)/log2级分割后重新排序

​ 一个N个数据长度的数据需要经过分割排序之后才能进行蝶形运算，引入上面的哪个图，

发现没有，在分割后，数据序列的位置发生了变化，而下面这个程序就是实现这一个过程。

void change()
{
	complex temp;
	unsigned short i=0,j=0,k=0;
	double t;
	for(i=0;i<size;i++)
	{
		k=i;
		j=0;
		t=(log(size)/log(2));  //算出序列的级数
		while( (t--)>0 )  //利用按位与以及循环实现码位颠倒
		{
			j=j<<1;
			j|=(k & 1);
			k=k>>1;
		}
		if(j>i)    //将x(n)的码位互换
		{
			temp=x[i];
			x[i]=x[j];
			x[j]=temp;
		}
	}
}

3、旋转因子Wn的表示

我们知道旋转因子在C语言中不好直接的表示出来，但是我们可以利用它的性质表示
$$W_N^k=e^{-j\frac{2\pi k}{N}}=cos(\frac{2\pi k}{N})-jsin(\frac{2\pi k}{N})$$
程序表示为

void transform()
{
	int i;
	W=(complex *)malloc(sizeof(complex) * size);//给指针分配size的空间 size是数据长度
	for(i=0;i<size;i++)
	{
		W[i].real=cos(2*PI/size*i);  //欧拉表示的实部
		W[i].imag=-1*sin(2*PI/size*i);  //欧拉表示的虚部
	}
}

4、复数的加、减、乘运算

上面也讲过复数的运算法则

加法：
$$Z_1+Z_2=(a+c)+(b+d)i$$
减法：
$$Z_1-Z_2=(a-c)+(b-d)i$$
乘法：
$$Z_1{Z}_2=(ac-bd)+(ad+bc)i$$
程序实现如下：

void add(complex a,complex b,complex *c)//定义结构体a、b和指针c    加法
{
	c->real=a.real+b.real; //c的目的是取出结构体中的数据
	c->imag=a.imag+b.imag;
}
void sub(complex a,complex b,complex *c)   //减法
{
	c->real=a.real-b.real;
	c->imag=a.imag-b.imag;
}
void mul(complex a,complex b,complex *c)   //乘法
{
	c->real=a.real*b.real - a.imag*b.imag;
	c->imag=a.real*b.imag + a.imag*b.real;
}

5、碟形运算

上面讲过
$$C_k=A_k+W_N^k{B}_k$$

$$C_{k+\frac{\pi }{2}}=A_k-W_N^k{B}_k$$

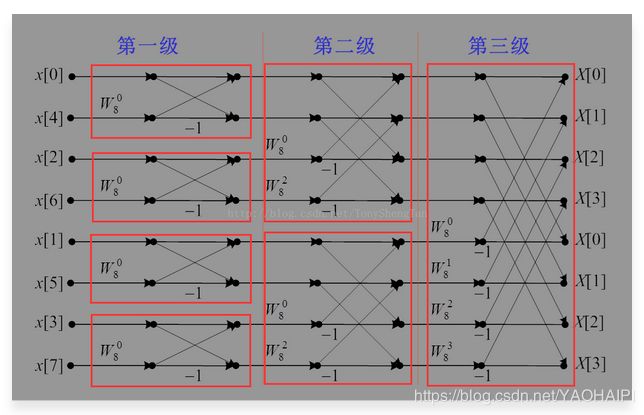
再来看8点蝶形运算的图形

第一级：蝶形系数均为
$$W_N^0$$
蝶形结点的距离为1.

第二级：蝶形系数为
$$W_N^0,W_N^{\frac{N}{2^2}}$$
蝶形结点的距离为2.

第三级：蝶形系数为
$$W_N^0,W_N^{\frac{N}{2^3}},W_N^{\frac{2N}{2^3}},W_N^{\frac{3N}{2^3}}$$
蝶形结点的距离为4.

第log(N)/log2级：蝶形系数为
$$W_N^0,W_N^1,......W_N^{\frac{N}{2}-1}$$
蝶形结点的距离为N/2

void fft()
{
	int i=0,j=0,k=0,m=0;
	complex q,y,z;
	change();
	for(i=0;i<log(size)/log(2) ;i++)  //蝶形运算的级数
	{
		m=1<<i;   //移位 每次都是2的指数的形式增加，其实也可以用m=2^i代替
		for(j=0;j<size;j+=2*m)  //一组蝶形运算，每一组的蝶形因子乘数不同
		{
			for(k=0;k<m;k++)  //蝶形结点的距离  一个蝶形运算 每个组内的蝶形运算
			{
				mul(x[k+j+m],W[size*k/2/m],&q);
				add(x[j+k],q,&y);
				sub(x[j+k],q,&z);
				x[j+k]=y;
				x[j+k+m]=z;
			}
		}
	}
}

6、总体程序

#include
#include
#include
#define N 1024
typedef struct{       //定义一个结构体表示复数的类型
	double real;
	double imag;
}complex;
complex x[N], *W;   //定义输入序列和旋转因子
int size=0;   //定义数据长度
double PI=4.0*atan(1); //定义π 因为tan(π/4)=1 所以arctan（1）*4=π，增加π的精度
void output()
{
	int i;
	for(i=0;i<size;i++)
	{	
		printf("%.4f",x[i].real);
		if(x[i].imag>=0.0001)
		{
			printf("+%.4fj\n",x[i].imag);
		}
		else if(fabs(x[i].imag)<0.0001)
		{
			printf("\n");
		}
		else
		{
			printf("%.4fj\n",x[i].imag);
		}
	}
}
void change()
{
	complex temp;
	unsigned short i=0,j=0,k=0;
	double t;
	for(i=0;i<size;i++)
	{
		k=i;
		j=0;
		t=(log(size)/log(2));
		while( (t--)>0 )
		{
			j=j<<1;
			j|=(k & 1);
			k=k>>1;
		}
		if(j>i)
		{
			temp=x[i];
			x[i]=x[j];
			x[j]=temp;
		}
	}
	output();
}
void transform()
{
	int i;
	W=(complex *)malloc(sizeof(complex) * size);
	for(i=0;i<size;i++)
	{
		W[i].real=cos(2*PI/size*i);
		W[i].imag=-1*sin(2*PI/size*i);
	}
}
void add(complex a,complex b,complex *c)
{
	c->real=a.real+b.real;
	c->imag=a.imag+b.imag;
}
void sub(complex a,complex b,complex *c)
{
	c->real=a.real-b.real;
	c->imag=a.imag-b.imag;
}
void mul(complex a,complex b,complex *c)
{
	c->real=a.real*b.real - a.imag*b.imag;
	c->imag=a.real*b.imag + a.imag*b.real;
}
void fft()
{
	int i=0,j=0,k=0,m=0;
	complex q,y,z;
	change();
	for(i=0;i<log(size)/log(2) ;i++)
	{
		m=1<<i;
		for(j=0;j<size;j+=2*m)
		{
			for(k=0;k<m;k++)
			{
				mul(x[k+j+m],W[size*k/2/m],&q);
				add(x[j+k],q,&y);
				sub(x[j+k],q,&z);
				x[j+k]=y;
				x[j+k+m]=z;
			}
		}
	}
}
int main()
{
	int i;
	printf("输入数据个数\n");
	scanf("%d",&size);//输入数据的长度（2的整数次幂）
	printf("输入数据的实部、虚部\n");
	for(i=0;i<size;i++)
	{
		scanf("%lf%lf",&x[i].real,&x[i].imag);  //输入复数的实部和虚部
	}
	printf("输出倒序后的序列\n");
	transform();//变换序列顺序
	fft();//蝶形运算
	printf("输出FFT后的结果\n");
	output();//输出结果
	return 0;
}

输出结果演示：

依然以序列{2，3，3，2}为例

之前计算步骤如下：
$$X[0]=2W_4^0+3W_4^0+3W_4^0+2W_4^0=10$$

$$X[1]=2W_4^0+3W_4^1+3W_4^2+2W_4^3=-1-i$$

$$X[2]=2W_4^0+3W_4^2+3W_4^4+2W_4^6=0$$

$$X[3]=2W_4^0+3W_4^3+3W_4^6+2W_4^9=-1+i$$

可以非常明显的看出程序运算结果正确。

总结

本次的C程序还有一些不够完善的地方，现在还只能简单的输入一个2的整数次幂长度的序列，下次将补充：输入一个连续的时域信号，经过FFT变换后，输出结果，并将结果用gunplot画出来。争取达到matlab中的fft函数效果。

再次强调：由于本人实在太菜，如果有什么错误或者不清楚的地方还请各位大佬指出！