统计学习方法——第六章logistic递归

        Logistic回归是统计学中的经典分类方法，最大熵是概率模型学习的一个准则，将其推广到分类问题得到最大熵模型，logistic回归模型与最大熵模型都是对数线性模型。

【Logistic回归-算法】

可参考博客

《统计学习方法》简述http://blog.csdn.net/BOBOyspa/article/details/78247157

讲解+代码

       http://blog.csdn.net/zouxy09/article/details/20319673?locationNum=6&fps=1

基本讲解

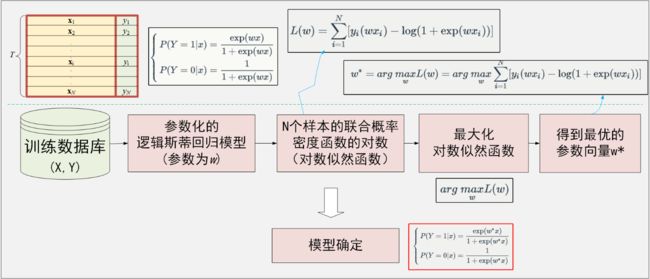
       如下图，logistic（逻辑斯谛）回归模型的引入、模型的参数估计（极大对数似然估计以及梯度下降法）：

最终类别的判定

       对于给定的样本x，利用二项逻辑斯蒂回归模型计算该样本类别为1和0的概率，然后，将样本x分类到概率较大的那一类。

       将h=0.5作为一个阀值，当估计值大于0.5时把样本分为1类，估计值小于0.5时把样本分为0类。

*logistic回归 VS logistic回归：

       logistic回归实际上就是对线性回归多增加了一个函数映射，使其值域由无穷区间映射到[0,1]区间。实现此功能需要在输出加一个logistic函数。

算法流程如下：

书上算法：

参数估计：

       对数似然函数，将L(w)作为损失函数，用随机梯度下降的方法求解；每次随机选取一个误分类点，用上述梯度对w进行更新。

 

【代码】   from机器学习实战

       可参考的另一个博客 http://blog.csdn.net/wds2006sdo/article/details/53084871

       逻辑斯谛回归模型正确率maybe优于感知器模型的，原因浮点数精度等问题。

Step1：载入数据

def loadData():
    train_x = []
    train_y = []

    with open('test_set.txt') as f:
        text = f.readlines()

    for line in text:
        train_x.append([1] + line.split()[:-1]) 
        train_y.append([line.split()[-1]]) #此处[[ ]]是为了方便转为数组
    return np.mat(train_x).astype(float),np.mat(train_y).astype(float)   #此处float便于后续计算

*Note1:

       当对array进行约简运算时,经常二维数组变成一维array;运算时会broadcast效果,可能报错;所以此处用matrix类型。

Step2：训练

1）计算sigmoidfunction

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

2）训练

def trainLogRegres(train_x,train_y,opts):
    numSample,numFeature = train_x.shape    #样本数numSample,特征数numFeature
    weights = np.ones((numFeature,1))
    
    maxIter = opts['maxIter']
    alpha = opts['alpha']
    for k in range(maxIter):
        if opts['optimizeType'] == 'gradDescent':   ## gradient descent algorilthm 
            output = sigmoid(train_x * weights) #train_x:(numSample,numFeature)
            error = train_y - output    #error:(numSample,1)
            weights += alpha * train_x.transpose() * error
        elif opts['optimizeType'] == 'stocGradDescent':     #stochastic gradient descent
            for i in range(numSample):
                alpha = 4 / (10 + k + i)   #约束
                output = sigmoid(train_x[i] * weights)    #train_x[i]:(1,numFeature)  weights:(numFeature,1)
                error = train_y[i] - output     #error：(1,1)
                weights += alpha * train_x[i].transpose() * error
        elif opts['optimizeType'] == 'min-batch-gradDescent':   #set b = 10
            b = 10
            for i in range(0,b,numSample):
                output = sigmoid(train_x[i:i+b] * weights)   #train_x[i]:(b,numFeature)
                error = train_y[i:i+b] - output    #error:(numSample,1)
                weights += alpha * train_x[i:i+b].transpose() * error
        else:
            raise NameError('Not support optimize method type!') 
    return weights

Step3：测试

def testLogRegres(weights, test_x, test_y):
      
    output = sigmoid(test_x * weights)
    predict = output > 0.5
    
    accuracy = sum(predict == test_y)/len(test_y)
    return accuracy

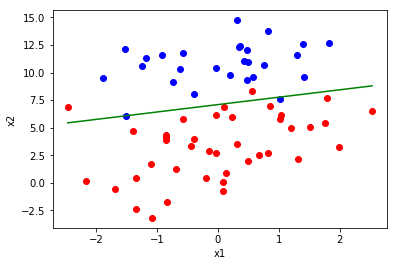
Step4：可视化

def showLogRegres(weights, train_x, train_y):
    for i in range(len(train_y)):
        if train_y[i] == 1:
            plt.plot(train_x[i,1], train_x[i,2],'or')
        else:
            plt.plot(train_x[i,1], train_x[i,2],'ob')
        
    min_x = float(min(train_x[:,1]))
    max_x = float(max(train_x[:,1]))
    min_y = (- weights[0,0] - weights[1,0] * min_x) / weights[2,0]  #注意此处x2和x1的关系
    max_y = (- weights[0,0] - weights[1,0] * max_x) / weights[2,0]
    plt.plot([min_x,max_x],[min_y,max_y],'g-')	#绘制分割线
        
    plt.xlabel('x1')
    plt.ylabel('x2')

主函数

import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_validation import train_test_split

if __name__ == '__main__':
    ##step1：load data
    print('step1:Start loading data...')
    time_1 = time.time()
    
    train_set,train_label = loadData()
    train_x,test_x,train_y,test_y = train_test_split(train_set,train_label,test_size=0.33, random_state=23323)
    
    time_2 = time.time()
    print('      Loading data costs %f seconds.\n'%(time_2 - time_1))
    
    ##step2：training...
    print('step2:Start training...')
    opts = {'alpha': 0.01, 'maxIter': 100, 'optimizeType': 'stocGradDescent'}  
    optimalWeights = trainLogRegres(train_x,train_y,opts)
    
    time_3 = time.time()
    print('      Training data costs %f seconds.\n'%(time_3 - time_2))
    ##step3：testing...
    print('step3:Start testing...')
    accuracy = testLogRegres(optimalWeights, test_x, test_y)
    print('      accuracy:%f'%accuracy)
    
    time_4 = time.time()
    print('      Testing data costs %f seconds.\n'%(time_4 - time_3))
    
    ##step4：plot the figure...
    print('step4:Start plotting the figure...')
    showLogRegres(optimalWeights, train_x, train_y)
    
    time_4 = time.time()
    print('      Plotting the figure costs %f seconds.\n'%(time_4 - time_3))

输出

step1:Start loading data...
      Loading data costs 0.001000 seconds.


step2:Start training...
      Training data costs 0.057000 seconds.


step3:Start testing...
      accuracy:0.969697
      Testing data costs 0.001000 seconds.


step4:Start plotting the figure...
      Plotting the figure costs 0.112000 seconds.