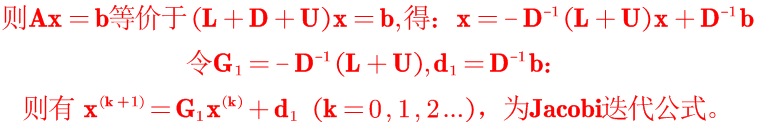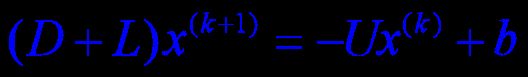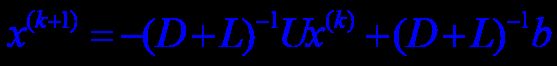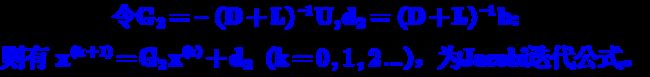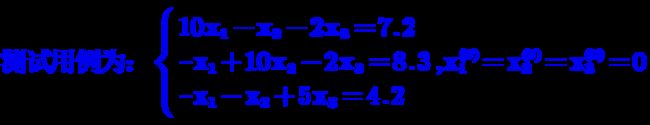利用Python,实现雅克比(Jacobi)迭代法以及高斯-塞德尔(G-S)迭代法【矩阵形式】
利用Python,实现雅克比(Jacobi)迭代法以及高斯-塞德尔(G-S)迭代法【矩阵形式】
本文讲解使用Jacobi迭代和G-S迭代算法求解方程组的Python代码实现,同时涉及算法的原理阐述。
文章目录
- 【Jacobi算法原理】
- 【Jacobi的Python代码实现】
- 1.1输入自变量个数mu,方程个数nu,迭代误差精度e
- 1.2初始化LDU矩阵(p为行数,q为当前列数。)
- 1.3构建自变量初值X_Current矩阵
- 1.4初始化因变量y矩阵
- 1.5计算并得到G1,d1矩阵(参照前面的Jacobi迭代公式)
- 1.6将迭代计算公式放入循环中,当迭代误差达到e精度时,打印X的求解结果
- 【G-S算法原理】
- 【G-S的Python代码实现】
- 测试情况:
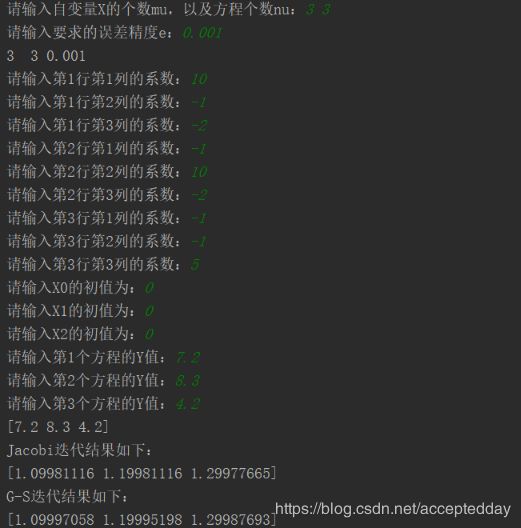
- 测试截图:
【Jacobi算法原理】
已知:现有n元线性方程组,如何通过代码实现该方程组的有解的判定,以及自变量求解?
矩阵形式如下:
设方程组Ax=b的系数矩阵A非奇异,且主对角元素aii≠0(i=1,2,…,n),则可将A分裂成:
【Jacobi的Python代码实现】
步骤如下:
1.1输入自变量个数mu,方程个数nu,迭代误差精度e
a = input("请输入自变量X的个数mu,以及方程个数nu:")
mu, nu = [int(i) for i in a.split(" ")]
b = input("请输入要求的误差精度e:")
e = float(b)
print(str(mu) + " " + str(nu)+" "+str(e))
1.2初始化LDU矩阵(p为行数,q为当前列数。)
L, D, U = [], [], [] # 初始化LDU矩阵
for p in range(nu):
L.append([]), D.append([]), U.append([])
for q in range(mu):
x_in = float(input("请输入第%d行第%d列的系数:" % (p + 1, q + 1)))
if p < q:
L[p].append(x_in), D[p].append(0), U[p].append(0)
elif p == q:
L[p].append(0), D[p].append(x_in), U[p].append(0)
else:
L[p].append(0), D[p].append(0), U[p].append(x_in)
L, D, U = np.array(L), np.array(D), np.array(U)
1.3构建自变量初值X_Current矩阵
X_Current = [] # 自变量x矩阵
for q in range(mu):
x_in = float(input("请输入X%d的初值为:" %q))
X_Current.append(x_in)
X_Current = np.array(X_Current).T # 将X行向量转置为列向量,便于后面矩阵的计算;
1.4初始化因变量y矩阵
b_Const = [] # 因变量y矩阵
for p in range(nu):
y_in = float(input("请输入第%d个方程的Y值:" % (p + 1)))
b_Const.append(y_in)
b_Const = np.array(b_Const).T # 将X行向量转置为列向量,便于后面矩阵的计算;
1.5计算并得到G1,d1矩阵(参照前面的Jacobi迭代公式)
L_U = copy.deepcopy(L)
for p in range(nu):
for q in range(mu):
L_U[p][q] = L[p][q]+U[p][q] # 将L与U按行,对应位置相加
G1 = np.dot(-np.linalg.inv(D), L_U) # np.linalg.inv(D)求矩阵的逆
d1 = np.dot(np.linalg.inv(D), b_Const)
1.6将迭代计算公式放入循环中,当迭代误差达到e精度时,打印X的求解结果
# x^(k+1) = G1*x^(k) + d1
X_New = copy.deepcopy(X_Current) # 导入copy库,深度拷贝X_Current作为X_New的初始化;
# Jacobi迭代
epoch = 0 # 迭代次数
while 1:
flag = 0 # 误差精度标记,统计达到精度要求的x数目,当X_New同一个epoch里所有的x迭代结果均达到精度时,输出X_New
X_Current = X_New
X_New = np.dot(G1, X_Current)
for p in range(mu):
X_New[p] = X_New[p] + d1[p]
if math.fabs(X_New[p]-X_Current[p]) < e:
flag += 1
epoch += 1
if epoch > 50: # 根据Jacobi迭代收敛特性,设定迭代上限为50次;
print("Jacobi迭代不收敛!")
epoch = 0
break
if flag == mu:
print("Jacobi迭代结果如下:")
print(X_New)
break
需要注意的地方:1.flag == mu,# 误差精度标记,统计达到精度要求的x数目,当X_New同一个epoch里所有的x迭代结果均达到精度时,输出X_New。2. epoch > 50,#根据Jacobi迭代收敛特性,设定迭代上限为50次,防止程序死锁;
【G-S算法原理】
即为矩阵形式求解的另一种迭代公式,推导过程与上述的Jacobi公式近似:
又因为|D|≠0,所以|D+L|≠0,故:
【G-S的Python代码实现】
与Jacobi代码实现近似,需要修改的部分如下:
# 计算D+L
D_L = copy.deepcopy(L)
for p in range(mu):
for q in range(nu):
D_L[p][q] = D[p][q]+L[p][q]
G2 = np.dot(-np.linalg.inv(D_L), U) # np.linalg.inv(D+L)求矩阵的逆
d2 = np.dot(np.linalg.inv(D_L), b_Const)