再看C++哈希表(散列表)
C++哈希表
- 哈希表的原理
- 哈希表描述
- 哈希冲突问题
- 闭散列法
- 哈希表的扩容问题
- 开散列
- 哈希表的迭代器
- unordered_map的模拟实现
依稀还记得上学期期末,数据结构课设的抽签中抽中了哈希表实现的电话号码查询系统,再回过头来看自己写的,好菜。。。
github程序链接https://github.com/duchenlong/Cpp/tree/master/Hash/Hash
因为红黑树在查找中的效率为O(log N),为了能够更为快速的查找数据,最好是趋于O(1)的时间复杂度。于是C++11中新加入了unordered_map和unordered_set两个容器,不同于map和set的是,map和set的底层是红黑树的接口,而unordered_map和unordered_set的底层是哈希表的接口,可以让查找效率无限接近于O(1)。
哈希表的原理
首先有这样一个问题,就是给定一串数据,再给一个数字num,怎么在O(1)的时间复杂度内判断num在那一串数据中有没有出现?

直接定制法(适用于数据范围比较小的时候)
因为是数据类型,如果数据的范围不是很大的话,我们就可以开辟数据范围大小的数组,让数组的下标位置就表示这个数据,那么我们就可以在O(1)的时间范围内判断出该数据有没有出现,只需判断arr[num] == num就可以知道答案了。
但是实际中,很有可能这个数据比较极端:
-
1,10000这种的,明明只有两个数据,却要我们开10000个数据的空间,就造成了很大程度的浪费; -
再比如
4,294,967,296这样的数据,表示的范围很大,我们在32位的系统中,就得开辟4G大小的空间,这有点不现实。 -
再一种就是
字符串(string)类型的数据,char类型的字符,我们还可以用ASCII码操作操作,但是字符串类型不能直接进行索引了。
对于字符串类型,处理方式比较简单,我们可以看成是一个个字符拼接而成的数据,依次相加每个字符的ASCII 码就可以操作了。
size_t ans = 0;
for (size_t i = 0; i < key.size(); i++)
{
ans *= 131;//玄学研究,*131可以很大程度上避免冲突
ans += key[i];
}
除留余数法
而对于其他两种情况,我们可以规定一个数组的大小,然后对这个数据取余就可以了pos = data % size,这样就可以保证之后的数据都是在这个数组中。
哈希表描述
对于哈希表的描述,我们可以这样来
template<class K, class T, class KOfT>
class HashTable
{
public:
HashTable()
:_num(0)
{
//初始的容量不能为0,
_table.resize(10);
}
private:
vector<HashData<T> > _table;
size_t _num;//所存储数据的数量
};
其中哈希表的数据类型,我们定义了一个结构体
//数组的类型
template<class T>
struct HashData
{
T _data;
Status _status;//当前位置的状态
};
又因为存在哈希冲突的问题,所以说我们在删除元素节点的时候,不能真正的删除掉,得采用惰性删除的方式。也就是给每一个结点定义三个状态,存在数据,不存在数据,删除数据
//哈希表中每一个位置的状态
enum Status
{
EMPTY,//空
EXITS,//存在
DELETE,//删除
};
而KOfT容器呢,是我们自定义的一个容器,他重载了(),作用就是获取计算权值的数据
因为这个数据不一定是数值类型,所以我们需要一个进行计算的模板
- 如果数据是数值类型,我们完全可以直接进行获取;
- 如果数据是字符串类型,我们就需要自己进行计算了。这就可以使用模板的特化进行解决
//得到当前位置的数据
template<class T>
struct _Hash
{
const T& operator()(const T& key)
{
return key;
}
};
//特化字符串类型数据
template<>
struct _Hash < string >
{
size_t operator()(const string& key)
{
size_t ans = 0;
for (size_t i = 0; i < key.size(); i++)
{
ans *= 131;
ans += key[i];
}
return ans;
}
};
在哈希表内部,我们写一个HashFunction函数来实现这一功能,根据数据来计算插入的位置
//得到当前位置的数据,转为数字类型
size_t HashFunc(const K& key)
{
Hash hash;
return hash(key);
}
哈希冲突问题
那么问题又来了,如果我们数组的大小是10,当我们依次插入 1 ,11,21的时候,经过计算,他们的插入位置都是pos = 1,这就发生了哈希冲突。
对于哈希冲突的问题,我们有着这样几种处理方式
闭散列法
闭散列法也叫开放定址法。当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个” 空位置中去。
问题又来了,如何找这个位置更好呢?
- 线性探测法
从发生冲突的位置开始,依次向后探测(如果到了数组的末尾,就需要来一个循环,从0号位置开始继续探测),直到寻找到下一个空位置为止
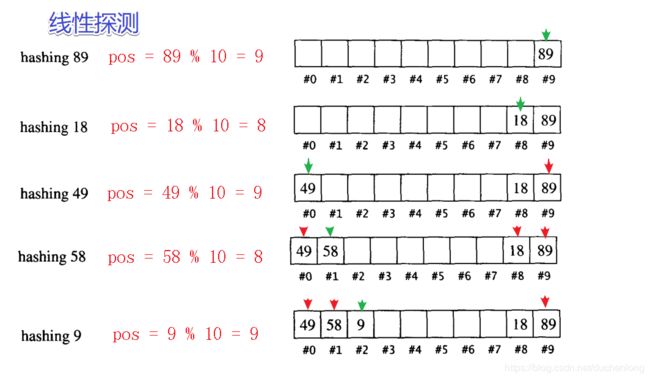
这样做有一个缺点,那就是如果连续插入几个相同pos的数据,很容易就会出现相同pos的数据进行扎堆的现象,也就是不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜索效率降低。
//线性探测
size_t idx = _koft(d) % _table.size();
while (_table[idx]._status == EXITS)
{
//如果该数据已经存在
if (_koft(_table[idx]._data) == _koft(d))
return false;
//向后查找的时候,需要组成一个循环查找
idx = (idx + 1) % _table.size();
}
_table[idx]._data = d;
_table[idx]._status = EXITS;
_num++;
- 二次探测
为了解决线性探测中,相同pos的数据扎堆出现的现象,二次探测如果发生了冲突,采取跳跃式的向后寻找插入位置。

这样由于指数增长的问题,如果直接访问的话,很快就会越界的,所以说还需要对数组的大小进行取模。
//二次探测
size_t start = _koft(d) % _table.size();
size_t idx = start;
int i = 1;
while (_table[idx]._status == EXITS)
{
if (_koft(_table[idx]._data) == _koft(d))
return false;
idx = start + i * i;
i++;
idx %= _table.size();
}
_table[idx]._data = d;
_table[idx]._status = EXITS;
_num++;
当数据在持续插入的情况下,我们很容易面对的一个问题就是 哈希表满了
哈希表的扩容问题
对于哈希表,我们是不能让这个表满了的,所以说,得在这个哈希表快要满的时候,就进行扩容,起码闭散列是这样的
这里又引入了一个新的概念,负载因子,就是元素的个数 除以 哈希表的大小,所得到的结果。所以说,负载因子在闭散列中只会是 0 - 1中间的数据。
而在闭散列中,当负载因子在0.7 或者 0.8的时候,就需要进行扩容了。
对于扩容,我之前在课设验收的时候就被老师问到了这个问题,当时写的扩容被老师一眼看出来问题所在(太强了),后来想了想,应该就是下面这种扩容方式
其实哈希表的扩容没有什么技巧可言,就是把所有的数据,全部再插入到新的哈希表中就可以了,新的哈希表的容量一般是旧的哈希表的2倍
这里又两种写法
- 第一种就是新建一个2倍大小的数组,然后手写插入函数
//是否需要扩容
if (_num * 10 / _table.size() >= 7)
{
//扩容
//第一种写法,建立一个vector
vector<HashData<T>> newTable;
newTable.resize(_table.size() * 2);
for (size_t i = 0; i < _table.size(); i++)
{
if (_table[i]._status == EXITS)
{
//计算在新表中的数据
size_t idx = _koft(_table[i]._data) % newTable.size();
//找到插入位置
while (newTable[idx]._status == EXITS)
idx = (idx + 1) % newTable.size();
newTable[idx]._data = _table[i]._data;
newTable[idx]._status = EXITS;
}
}
swap(newTable, _table);
}
- 新建一个哈希表,调用这个哈希表的插入函数,最后再交换两个哈希表底层的数组
//是否需要扩容
if (_num * 10 / _table.size() >= 7)
{
//扩容
//第二种写法,新建一个hashtable
HashTable<K, T, KofT<K>> newHash;
newHash._table.resize(_table.size() * 2);
for (size_t i = 0; i < _table.size(); i++)
if (_table[i]._status == EXITS)
newHash.Insert(_table[i]._data);
_table.swap(newHash._table);
}
开散列
开散列法又叫链地址法(开链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中

对于这样一个一个的桶,就不存在哈希冲突的问题了,我们先计算一个插入位置pos,那么这个位置所存储的都是这个pos权值的数据,他们以链表的形式连接在一起。(如果想要发散一下的话,也可以使用红黑树进行连接)
当我们在插入数据的时候,所选择的插入方式便是头插的方法
而在闭散列中,我们在负载因子=1 的时候进行扩容
//插入
pair<iterator, bool> insert(const T& data)
{
KeyOfT koft;
//桶哈希中,如果负载因子 = 1,就进行扩容
if (_table.size() == _num)
{
vector<node*> newTable;
size_t newSize = _table.size() * 2;
newTable.resize(newSize);
for (size_t i = 0; i < _table.size(); i++)
{
node* cur = _table[i];
while (cur != nullptr)
{
node* next = cur->_next;
//计算应该插入到新表中的位置
size_t idx = HashFunc(koft(cur->_data)) % newSize;
//进行头插
cur->_next = newTable[idx];
newTable[idx] = cur;
cur = next;
}
//这个节点以经没有数据了
_table[i] = nullptr;
}
_table.swap(newTable);
}
//插入这个新的数据
//计算插入位置
size_t idx = HashFunc(koft(data)) % _table.size();
//找到插入的地方
node* cur = _table[idx];
while (cur != nullptr)
{
//该数据已经在表中,不需要插入了
if (koft(cur->_data) == koft(data))
return make_pair(iterator(cur, this), false);
cur = cur->_next;
}
//确保表中没有该数据,进行头插
node* newNode = new node(data);
newNode->_next = _table[idx];
_table[idx] = newNode;
_num++;
return make_pair(iterator(newNode, this), true);
}
哈希表的迭代器
迭代器的框架
template<class K,class T,class KeyOfT,class Hash>
struct __HashTableIterator
{
typedef __HashTableIterator<K, T, KeyOfT, Hash> Self;
typedef HashTable<K, T, KeyOfT, Hash> HT;
typedef HashNode<T> node;
node* _node;
HT* _pht;
__HashTableIterator(node* n,HT* pht)
:_node(n)
, _pht(pht)
{}
};
我们所要实现的迭代器重要有*,->,++,==,!=
因为在++的操作中,如果出现下面这种情况
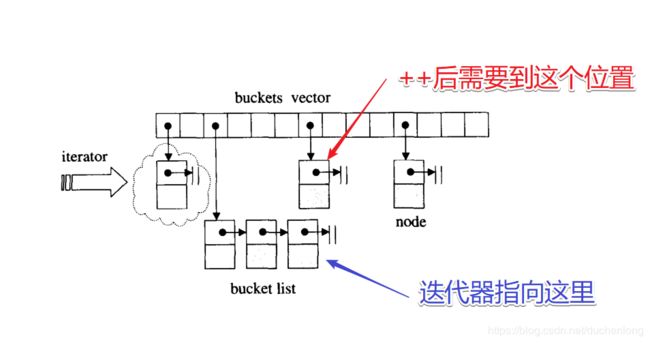
当我们把当前链表的数据都遍历完了,我们就需要到下一个pos位置去查找数据了。那么在查找的时候,我们需要访问的是这个哈希表的私有成员,所以我们就需要将迭代器设置为哈希表的友元。
//设置迭代器为自己的友元
friend struct __HashTableIterator < K, T, KeyOfT, Hash > ;
++的重载
Self operator++()
{
if (_node->_next != nullptr)
{
_node = _node->_next;
return *this;
}
//当前权值的桶已经走完了,需要找到下一个桶
KeyOfT koft;
size_t i = _pht->HashFunc(koft(_node->_data)) % _pht->_table.size();
i++;//到下一个桶的位置
for (; i < _pht->_table.size(); i++)
{
node* cur = _pht->_table[i];
if (cur)
{
_node = cur;
return *this;
}
}
_node = nullptr;//这里说明遍历完了最后一个桶
return *this;
}
unordered_map的模拟实现
他的底层是调用哈希表的接口,所以很多功能函数只是一个包装的作用,这里只是实现一下[]的重载
这是unordered_map的大体框架。
template<class K,class V,class Hash = _Hash<K> >
class unordered_map
{
//计算权值的数据的访问器
struct MapKOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
typedef typename HashTable<K, pair<K, V>, MapKOfT, Hash>::iterator iterator;
private:
HashTable<K, pair<K, V>, MapKOfT, Hash> _ht;
};
[]的重载,跟map是一个道理,我们只需要进行插入,然后返回第二个数据的引用就可以了
V& operator[](const K& key)
{
pair<iterator, bool> ans = _ht.insert(make_pair(key, V()));
return ans.first->second;
}

