时间序列模型(ARIMA和ARMA)完整步骤详述
老师作业要求,实现ARMA和ARIMA模型的基本全过程和最后结果。
目录
所用的所有数据包
1,数据准备与预处理
(1)数据准备
(2)数据预处理
2,数据重采样
3,平稳性和非白噪声
(1)差分法实现
(2)平滑法处理
(3)ADF检验
(4)非白噪声检验
4,时间序列定阶
(1)ACF和PACF定阶
5,构建模型和预测
(1)ARMA模型构建
(2)模型好坏检验
(3)ARIMA模型构建
总结
所用的所有数据包
import pandas as pd
import numpy as np
import seaborn as sns #热力图
import itertools
import datetime
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller #ADF检验
from statsmodels.stats.diagnostic import acorr_ljungbox #白噪声检验
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf #画图定阶
from statsmodels.tsa.arima_model import ARIMA #模型
from statsmodels.tsa.arima_model import ARMA #模型
from statsmodels.stats.stattools import durbin_watson #DW检验
from statsmodels.graphics.api import qqplot #qq图1,数据准备与预处理
(1)数据准备
自己做了点数据,做数据的代码如下:
def genertate_data():
index = pd.date_range(start='2018-1-1',end = '2018-9-1',freq='10T')
index = list(index)
data_list = []
for i in range(len(index)):
data_list.append(np.random.randn())
dataframe = pd.DataFrame({'time':index,'values':data_list})
dataframe.to_csv('C:\\Users\\happy\\Desktop\\old_data.csv',index=0)
print('the data is existting')
然后将它保存在了old_data.csv中,然后故意去将文件夹中的某些值,改成了-10000,弄成了异常值,(因为老师说尽可能显得步骤完整,最后分数才会高-,-所以我自己手动添加异常)
(2)数据预处理
这块的主要工作就是利用pandas里面的函数,去查看一下刚特殊操作后的数据。
def data_handle():
data = pd.read_csv('C:\\Users\\happy\\Desktop\\old_data.csv')
#print(data.describe()) #查看统计信息,发现最小值有-10000的异常数据
#print((data.isnull()).sum()) #查看是否存在缺失值
#print((data.duplicated()).sum()) #重复值
def change_zero(x):
if x == -10000:
return 0
else :
return x
data['values'] = data['values'].apply(lambda x: change_zero(x))
#利用均值填充缺失值
mean = data['values'].mean()
def change_mean(x):
if x == 0:
return mean
else:
return x
data['values'] = data['values'].apply(lambda x: change_mean(x))
#保存处理过的数据
data.to_csv('C:\\Users\\happy\\Desktop\\new_data.csv',index=0)
print('new data is existing')2,数据重采样
为了得高分(-,-),做了很多个数据,然后一共有34992个数据,然后进行了一下重采样,数据以天进行重采样。
def Resampling(): #重采样
df = pd.read_csv('C:\\Users\\happy\\Desktop\\new_data.csv')
#将默认索引方式转换成时间索引
df['time'] = pd.to_datetime(df['time'])
df.set_index("time", inplace=True)
data = df['2018-1-1':'2018-8-1'] #取18-1-1到8-1做预测
test = df['2018-8-1':'2018-9-1']
data_train = data.resample('D').mean() #以一天为时间间隔取均值,重采样
data_test = test.resample('D').mean()
return data_train,data_test3,平稳性和非白噪声
由于ARMA和ARIMA需要时间序列满足平稳性和非白噪声的要求,所以要用查分法和平滑法(滚动平均和滚动标准差)来实现序列的平稳性操作。一般情况下,对时间序列进行一阶差分法就可以实现序列的平稳性,有时需要二阶查分。
(1)差分法实现
def stationarity(timeseries): #平稳性处理
#差分法(不平稳处理),保存成新的列,1阶差分,dropna() 删除缺失值
diff1 = timeseries.diff(1).dropna()
diff2 = diff1.diff(1) #在一阶查分基础上做二阶查分
diff1.plot(color = 'red',title='diff 1',figsize=(10,4))
diff2.plot(color = 'black',title='diff 2',figsize=(10,4))
可以看一下图
一阶差分基本就满足了平稳性需要。
(2)平滑法处理
#滚动平均(平滑法不平稳处理)
rolmean = timeseries.rolling(window=4,center = False).mean()
#滚动标准差
rolstd = timeseries.rolling(window=4,center = False).std()
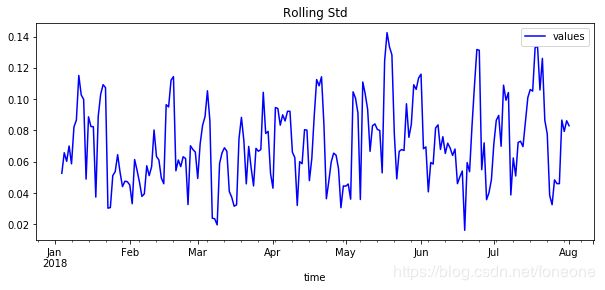
rolmean.plot(color = 'yellow',title='Rolling Mean',figsize=(10,4))
rolstd.plot(color = 'blue',title='Rolling Std',figsize=(10,4))处理结果如图所示。
可以看出,平滑法不太适合我造出来的数据,一般情况下,这种方法更适合带有周期性稳步上升的数据类型。
(3)ADF检验
除了上述两种对于时间序列的处理方法之外,还有一种以数据的方式呈现的平稳性检验方法:ADF检验。
#ADF检验
x = np.array(diff1['values'])
adftest = adfuller(x, autolag='AIC')
print (adftest) 结果如下:
如何确定该序列能否平稳呢?主要看:
(1)1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较,ADF Test result同时小于1%、5%、10%即说明非常好地拒绝该假设,本数据中,adf结果为-6.9, 小于三个level的统计值。
(2)P-value是否非常接近0.本数据中,P-value 为 7.9e-10,接近0。
ADF结果如何查看参考了这篇博客:
https://blog.csdn.net/weixin_42382211/article/details/81332431
(4)非白噪声检验
#纯随机性检验(白噪声检验)
p_value = acorr_ljungbox(timeseries, lags=1)
print (p_value)结果如图:
![]()
统计量的P值小于显著性水平0.05,则可以以95%的置信水平拒绝原假设,认为序列为非白噪声序列(否则,接受原假设,认为序列为纯随机序列。)
由于P值为0.315远大于0.05所以接受原假设,认为时间序列是白噪声的,即是随机产生的序列,不具有时间上的相关性。(解释一下,由于老师没有给数据,所以只能硬着头皮,假设它是非白噪声的做)
4,时间序列定阶
定阶用到了ACF和PACF判断模型阶数、信息准则定阶(AIC、BIC、HQIC)、热力图定阶。
(1)ACF和PACF定阶
直接采用步骤3的一阶差分后的数据来进行定阶操作。
def determinate_order(timeseries):
#利用ACF和PACF判断模型阶数
plot_acf(timeseries,lags=40) #延迟数
plot_pacf(timeseries,lags=40)
plt.show()结果如图所示:
上面分别是ACF和PACF的图,至于如何定阶不详细叙述了。一般是通过截尾和拖尾来确定阶数。目前还没有看到总结的比较好的文章。
(2)信息准则定阶
由于要通过ACF和PACF图来定阶,是一种看图的方法,因此可以计算AIC等值,来进行定阶。
#信息准则定阶:AIC、BIC、HQIC
#AIC
AIC = sm.tsa.arma_order_select_ic(timeseries,\
max_ar=6,max_ma=4,ic='aic')['aic_min_order']
#BIC
BIC = sm.tsa.arma_order_select_ic(timeseries,max_ar=6,\
max_ma=4,ic='bic')['bic_min_order']
#HQIC
HQIC = sm.tsa.arma_order_select_ic(timeseries,max_ar=6,\
max_ma=4,ic='hqic')['hqic_min_order']
print('the AIC is{},\nthe BIC is{}\n the HQIC is{}'.format(AIC,BIC,HQIC))一般都是一个一个运行,最好不要一起运行,结果出来的太慢了。
(3)热力图定阶
其实热力图定阶的方式和(2)信息准则定阶的方式类似,只是用热力图的方式呈现了。
#设置遍历循环的初始条件,以热力图的形式展示,跟AIC定阶作用一样
p_min = 0
q_min = 0
p_max = 5
q_max = 5
d_min = 0
d_max = 5
# 创建Dataframe,以BIC准则
results_aic = pd.DataFrame(index=['AR{}'.format(i) \
for i in range(p_min,p_max+1)],\
columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
# itertools.product 返回p,q中的元素的笛卡尔积的元组
for p,d,q in itertools.product(range(p_min,p_max+1),\
range(d_min,d_max+1),range(q_min,q_max+1)):
if p==0 and q==0:
results_aic.loc['AR{}'.format(p), 'MA{}'.format(q)] = np.nan
continue
try:
model = sm.tsa.ARIMA(timeseries, order=(p, d, q))
results = model.fit()
#返回不同pq下的model的BIC值
results_aic.loc['AR{}'.format(p), 'MA{}'.format(q)] = results.aic
except:
continue
results_aic = results_aic[results_aic.columns].astype(float)
#print(results_bic)
fig, ax = plt.subplots(figsize=(10, 8))
ax = sns.heatmap(results_aic,
#mask=results_aic.isnull(),
ax=ax,
annot=True, #将数字显示在热力图上
fmt='.2f',
)
ax.set_title('AIC')
plt.show() 图如下所示:
黑色的位置最好,可以看出p,q取(1,1)(3,1)(1,4)都可以。一般情况下是越小越好。
热力图实现过程参考了下面这篇博客(找不见了=,=)如果有侵权,请告知,会删除博文。
5,构建模型和预测
(1)ARMA模型构建
def ARMA_model(train_D,train,test,order):
arma_model = ARMA(train,order) #ARMA模型
result = arma_model.fit()#激活模型
#print(result.summary()) #给出一份模型报告
############ in-sample ############
pred = result.predict()
#pred.plot()
#train.plot()
#print('标准差为{}'.format(mean_squared_error(train,pred)))
#残差
resid = result.resid
#利用QQ图检验残差是否满足正态分布
plt.figure(figsize=(12,8))
qqplot(resid,line='q',fit=True)
#利用D-W检验,检验残差的自相关性
print('D-W检验值为{}'.format(durbin_watson(resid.values)))说明:train_D是重采样之后的数据,train是一阶查分后的,test是train样本外的数据,order给的是(1,1)通过定阶得到的。
以上都是通过参数传递进来的,没有在里面写。
预测过程有两种预测方式,一种是样本内的预测,一种是样本外的预测。意思就是,一个是根据train数据集的时间,在这个时间段内进行预测;样本外预测就是train的是2018-1-1到8-1的,但是要预测的是8-1到9-1的情况,是out-sample预测,一般情况下,out-sample是我们想要的,而不是样本内的预测。样本外的预测代码如下:
pred_one = result.predict(start=len(train)-5,end = len(train)+30, \
dynamic=True)
#print(pred_one)
#print(len(test))
#print(pred_one[6:-1])
#pred_one.plot()
#test.plot()
print('标准差为{}'.format(mean_squared_error(test,pred_one[6:-1],sample_weight=None,\
multioutput='uniform_average'))) #标准差(均方差)预测为样本内外是由dynamic参数决定的,特别注意:样本外的预测也要从样本内的某一个时间点开始才能进行预测。
在求解标准差的时候,要注意数据对齐。
(2)模型好坏检验
#残差
resid = result.resid
#利用QQ图检验残差是否满足正态分布
plt.figure(figsize=(12,8))
qqplot(resid,line='q',fit=True)
#利用D-W检验,检验残差的自相关性
print('D-W检验值为{}'.format(durbin_watson(resid.values)))用残差来检验模型的好坏,上述代码在创建模型里面面已经写过了,
qq图如下所示:
通过qq图可以看出,残差基本满足了正态分布。
D-W检验结果为:
![]()
当D-W检验值接近于2时,不存在自相关性,说明模型较好。
D-W检验如何数学说明,可以参考下面链接。
https://wenku.baidu.com/view/57224dcfcf84b9d528ea7aba.html
(3)ARIMA模型构建
创建模型的代码基本同上,只不过ARIMA有三个参数:p,d,q。其中p和q可以参考定阶的方法确定。d指的是用了多少阶差分,在我的模型中运用了一阶差分,因此d=1。
由于预测都是针对的差分法后的数据做的预测,但是真实数据并不是那样的,因此我还对差分后的数据进行还原操作。
看一下通过预测与实际真实值对比,模型到底是否很好。
def string_toDatetime(string):
return datetime.datetime.strptime(string, "%Y-%m-%d %H:%M:%S")
def ARIMA_model(train_H,train,test):
arima_model = ARIMA(train,order =(1,1,1)) #ARIMA模型
result = arima_model.fit()
#print(result.summary()) #给出一份模型报告
########得到训练集的预测时间序列#########
pred = result.predict()
#######还原#########
##2018-8-1 00:00 到 2018-9-1 00:00 ###
#将差分后的序列还原,pred_restored为还原之后
idx = pd.date_range(string_toDatetime('2018-8-1 00:00:00'),periods=len(pred[4:20]),freq='D')
pred_list= []
for i in range(len(pred[4:20])):
pred_list.append(np.array(pred)[i+4])
pred_numpy = pd.Series(np.array(pred_list),index=idx)
pred_restored = pd.Series(np.array(train_H)[5][0],\
index=[train_H.index[5]]).append(pred_numpy).cumsum()
x1 = np.array(pred_restored)
x2 = np.array(train_H[5:22])
y = []
for i in range(len(pred_restored)):
y.append(i+1)
y = np.array(y)
fig1 = plt.figure(num=2, figsize=(10,4),dpi=80)
plt.plot(y,x1,color='blue')
plt.plot(y,x2,color='red')
plt.ylim(0,0.8)
plt.show()代码里面对差分法后的进行还原,主要是下面这行代码:
pred_restored = pd.Series(np.array(train_H)[5][0],\
index=[train_H.index[5]]).append(pred_numpy).cumsum()主要用到了的是cumsum()这个函数,这个函数作用不再赘述,自行百度吧。
总结
关于ARMA和ARIMA模型,从数据处理到最后建模实现,就完成了。
但是,里面其实有一个很大的问题,就是当数据不是平稳性的数据的时候,用到了差分法进行处理,用到了dropna()这个函数,这个函数的意思是去掉序列中nan(在这个了里面是0)。因此当序列中两列相邻值相等时,就会去掉前面那一列,因此处理后的数据可能不是按照每一天的数据分布的,但是预测出来的是每一天都存在的。
如果不加dropna()这个函数的话,定阶那些都会报错(错误信息是存在nan值),但是模型不会报错。因此这块是一个存在的问题,还亟待处理,但是我看了很多的文章,对于这里好像没有过多深入的研究。
整篇博客都是代码实现的,具体的数学公式,自行百度吧~~