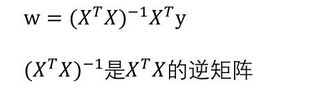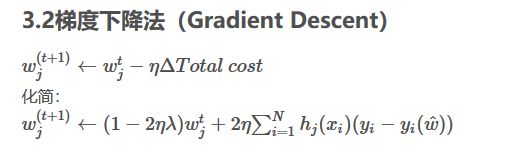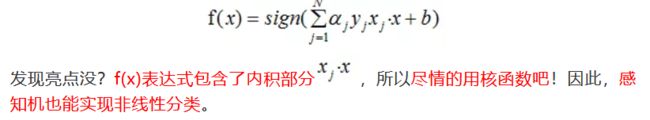机器学习笔记--持续更新
文章目录
- 1、线性回归的标准方程解法(又称最小二乘法)
- 2、LASSO算法与岭回归
- (1)Lasso回归的求解
- (2)岭回归求解
- (3)关于L1 、L2正则化的区别(形象通俗理解)
- (4)如何理解:一般线性回归是无偏估计,而Ridge回归是有偏估计
- (5)Lasso和PCA的区别
- (6)Lasso的应用场景
- 3、方差与偏差含义
- 4、K折交叉验证(k-fold cross validation)
- 5、监督学习假设输入与输出的随机变量X和Y遵循联合概率分布P(X,Y)
- 6、LR与SVM的时间复杂度对比
- 7、交叉验证(cross validation)
- 8、Roc曲线与PR曲线
- 9、BN
- (1)BN遇到relu激活函数如何工作?
- (2)为什么需要独立同分布?
- (3)BN的原理的最新解释
- 10、线性回归的推广:多项式回归
- 11、线性模型和树模型的区别
- 12、逻辑回归
- (1)逻辑回归中的One vs Rest 与softmax分类器适用场景
- (2)逻辑回归的损失函数、softmax回归的损失函数与交叉熵的损失函数
- (3)一个分类算法为什么为叫做逻辑回归?
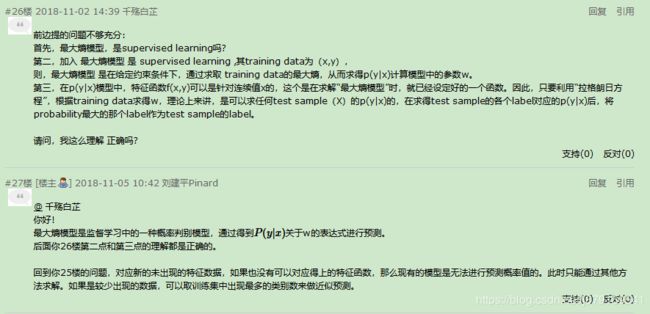
- (4)逻辑回归训练和测试时候的特征预处理的不一致性
- (5)逻辑回归的损失函数可视化
- 13、感知机模型
- (1)模型定义
- (2)损失函数
- (3)需要注意的两个点
- (4)感知机模型与逻辑回归的异同点
- 14、频率学派与贝叶斯学派对概率定义的不同
- 15、为什么选择β分布作为先验分布
- 16、分类问题中的判别式模型和生成性模型
- 17、KNN
- (1)K值的选择
- (2)KD树的搜索过程还不太理解
- (3)KNN算法的优缺点
- (4)数据是否为线性可分的以及如何选择不同的模型
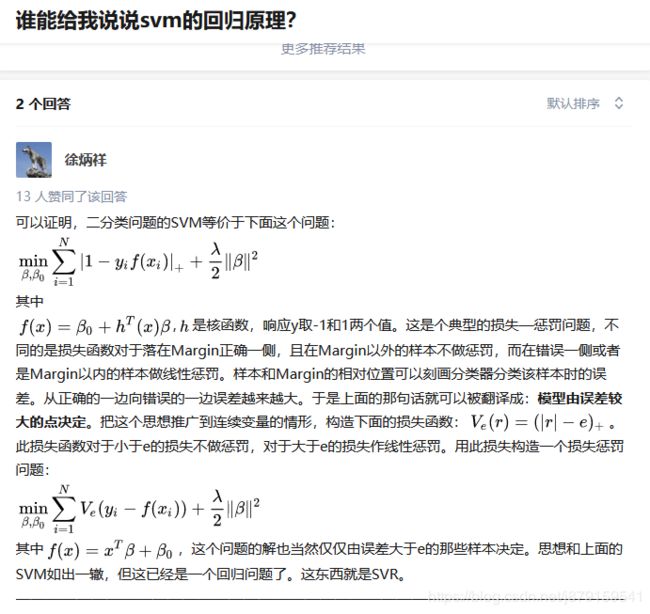
- 18、SVM
- (1)支持向量机种类
- (2)SVM从零开始推导公式
- (3)SVM的思想起源
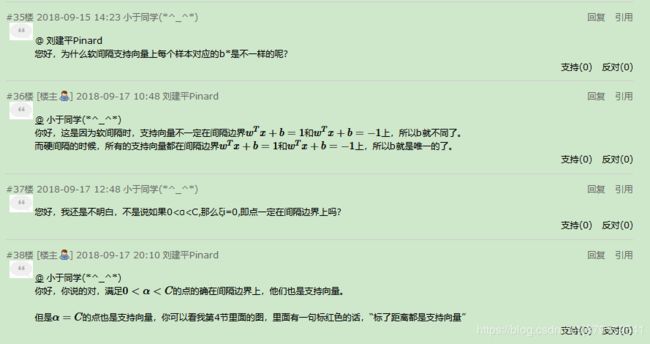
- (4)软间隔时的a的取值范围
- (5)软间隔和硬间隔时的b是否唯一
- (6)软间隔最大化时样本点位置的判断
- (7)核函数的意义
- (8)Ei的更新过程
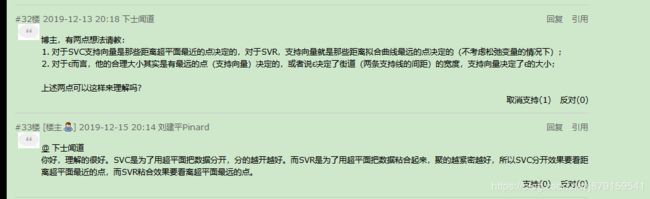
- (9)SVC与SVR的区别
- (10)SVM里的C
- (11)SVC与SVR通过合页损失函数进行统一
- (12)
- 19、决策树
- (1)图示ID3决策树算法流程
- (2)以信息增益作为评价标准偏向于选择较多的特征
- (3)决策树C4.5中的连续特征离散化
- (4)CART回归树和CART分类树的建立和预测的区别
- (5)决策树不用对特征做标准化预处理
- (6)决策树如何并行计算
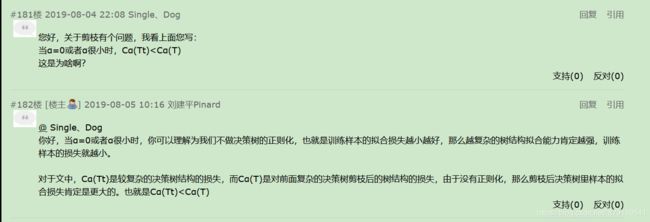
- (7)CART决策树进行剪枝的小疑问
- 20、贝叶斯算法
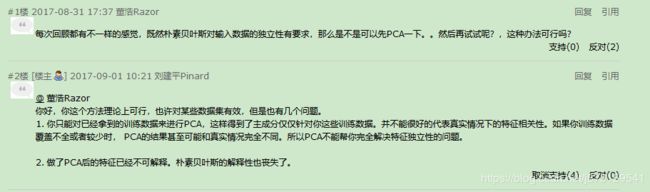
- (1)既然朴素贝叶斯对输入数据的独立性有要求,那么是不是可以先PCA一下
- (2)条件概率分布与条件概率分布的某一个概率值
- (3)通俗例子讲解朴素贝叶斯求解过程
- (4)
- 21、最大熵模型
- (1)算法流程的简单理解
- (2)逻辑回归与最大熵
- (3)机器学习面试之最大熵模型(通俗易懂)
- (4)方差与熵的关系
- (5)各种熵之间的关系
- (6)
- 22、集成学习概述
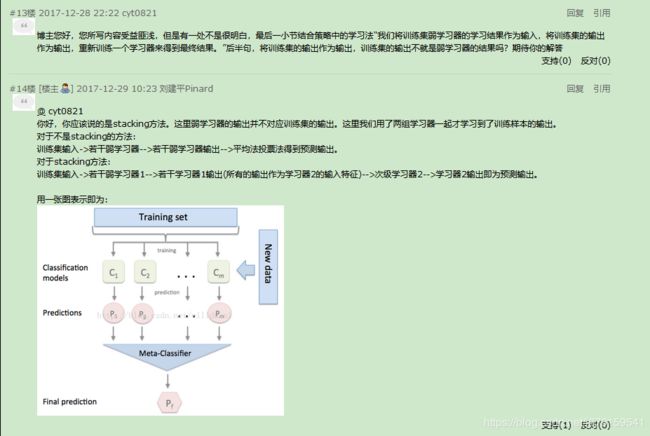
- (1)结合策略之stacking(学习法)
- (2)集成学习防止过拟合
- (3)样本权重如何处理
- (4)
- 23、GBDT
- (1)adaboost和GBDT的不同
- (2)随机森林与GBDT对异常点的处理
- (3)对数损失函数是如何度量损失的?
- (4)
1、线性回归的标准方程解法(又称最小二乘法)
下面是算w的解:
关于最小二乘法的讨论:
最小二乘法不是用来构造目标函数的方法么?我的看最后一段直接用最小二乘法与梯度下降法进行对比,我个人觉得应该是最小二乘法的矩阵解法与梯度下降法进行对比。梯度下降法可以用于求解最小二乘问题(线性和非线性都可以)。这里如果把最小二乘看做是优化问题的话,那么梯度下降算是求解方法的一种,矩阵解法是求解线性最小二乘的一种,高斯-牛顿法和Levenberg-Marquardt则能用于求解非线性最小二乘。
2、LASSO算法与岭回归
注:Lasso全名为Least Absolute Shrinkage and Selection Operator
(1)Lasso回归的求解
第一种解法**:坐标轴下降法,**顾名思义,是沿着坐标轴的方向去下降,这和梯度下降不同。梯度下降是沿着梯度的负方向下降。不过梯度下降和坐标轴下降的共性就都是迭代法,通过启发式的方式一步步迭代求解函数的最小值。
第二种解法**:最小角回归法,**对前向梯度算法和前向选择算法做了折中,保留了前向梯度算法一定程度的精确性,同时简化了前向梯度算法一步步迭代的过程。
参考博客:https://www.cnblogs.com/pinard/p/6018889.html
(2)岭回归求解
注:2w那里少了一个纳姆达
注:RSS是没加岭回归之前的代价函数,就是J(θ),H即为X
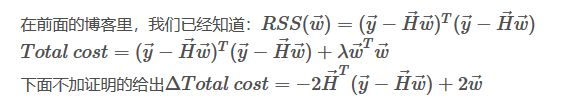
下面是梯度下降法的岭回归:(注意纳姆达加在了什么位置)
注意:岭回归对参数θ进行正则化的时候,θ0不参与,θ0相当于是截距,不被惩罚
当然也可以被惩罚,此时需要将y进行0均值化
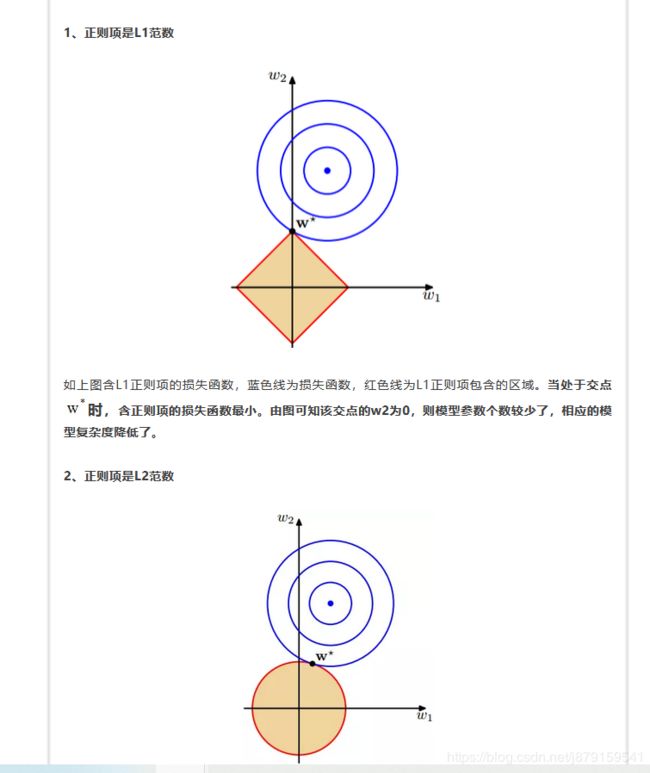
(3)关于L1 、L2正则化的区别(形象通俗理解)
贝叶斯定理的后验分布与似然函数和先验分布相关,不考虑先验分布时,则损失函数不包含正则化;考虑先验分布时,则损失函数包含正则化(先验分布是高斯分布时,相当于正则化项时L2;先验分布是拉普拉斯分布时,相当于正则化项是L1);最大化后验分布等同于最小化正则化的损失函数。
(4)如何理解:一般线性回归是无偏估计,而Ridge回归是有偏估计
无偏性意味着我们根据样本求得的参数期望等于总体分布的参数。对于线性回归,无偏性意味着根据样本求得的回归系数的期望等于总体分布的回归系数。
(5)Lasso和PCA的区别
Lasso和PCA都可以用于筛选特征并降维。但是Lasso是直接将不重要的特征丢弃,而PCA是将所有的特征放在一起综合考虑,降维后的特征已经和之前的原始特征不能一一对应的。
如果你的目的是筛选特征,并且降维后有解释性,那么就使用Lasso来筛,如果你的目的只是降维并训练模型,解释性要求不高,那么使用PCA。
(6)Lasso的应用场景
一般来说,对于高维的特征数据**,尤其线性关系是稀疏的,**我们会采用Lasso回归。或者是要在一堆特征里面找出主要的特征,那么Lasso回归更是首选了。但是Lasso类需要自己对α调优,所以不是Lasso回归的首选,一般用到的是下一节要讲的LassoCV类。
稀疏线性关系的意思就是绝大多数的特征和样本输出没有关系,线性拟合后这些特征维度的系数会全部为0,只有少量和输出相关的特征的回归系数不为0,这就是“稀疏线性关系”。
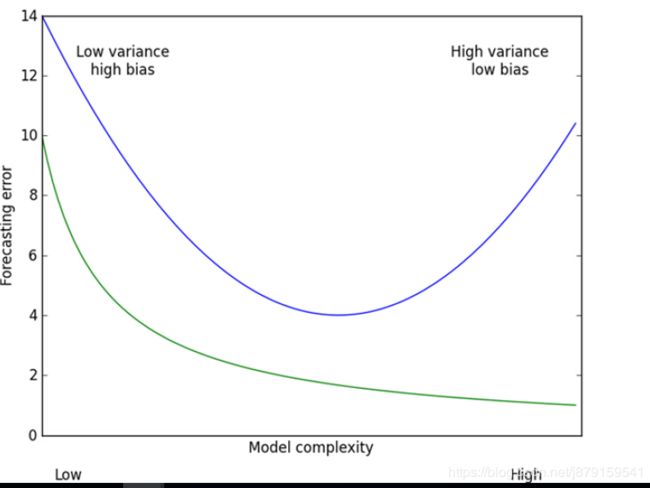
3、方差与偏差含义
error=bias+variance
bias:指的是模型在样本上的输出与真实值的误差。
variance:指的是每个模型的输出结果与所有模型平均值(期望)之间的误差。
方差大则过拟合,偏差大则欠拟合
过拟合的一种情况:**当线性回归的系数向量间(即模型参数)差异比较大时,**则大概率设计的模型处于过拟合了。用数学角度去考虑,若某个系数很大,对于相差很近的x值,结果会有较大的差异,这是较明显的过拟合现象。
4、K折交叉验证(k-fold cross validation)
当数据量比较小的时候,我们可能没有足够的数据分为training set,validation set, test set。
我们可以先把数据分为training set和test set,然后我们把training set均分为K份,交叉验证的步骤如下:
for k=1, 2, 3 … … , K:
每次选择第k个作为validation set,其余的作为training set,拟合得到w(k)
计算拟合模型在validation的误差errork(λ)
完成循环后计算平均误差:CV(λ)=1/K∑K(k=1)errork(λ)
选择CV最小的确定我们需要的λ。
K一般选取5或者10
5、监督学习假设输入与输出的随机变量X和Y遵循联合概率分布P(X,Y)
如何理解这句话??
其实就是假设输入特征X和输出Y之间是有联系,可以通过一些数据找到两者之间的规律和关系。
如果X和Y完全独立,那么P(Y|X) = P(Y),这样就无法通过训练数据找到X和Y的关系,进而也不能使用监督学习来学习这个模型。
6、LR与SVM的时间复杂度对比
对于梯度下降的复杂度,假设我们说的是BGD,那么假设我们有m个样本,n个特征,迭代T轮(不考虑提前终止),则时间复杂度约为O(mnT)。
LR基于梯度下降,所以时间复杂度也约是O(mnT)。
SVM复杂度主要在SMO算法,要看迭代轮数T, 样本数n,假设选择 α 每次需要扫所有的样本,则复杂度约为O(Tnn)
7、交叉验证(cross validation)
按你说的Kfold分10组,那么每次取其中9组做为训练集,1组作为验证集,一共10种组合,每种组合在训练集训练完毕后,在验证集会得到一个评估分数,最终我们在10组评估分数中选择最大的评估分数,对应的训练集模型参数即为我们需要的模型参数。(此处的模型参数不包括超参数,不同的超参数某种意义上已经属于不同的模型了;此处的模型参数只是一些w,比如卷积核的参数)
(1)一般S折都是评价一个模型好坏的,只是每一折得到的模型参数不同,对验证集的验证效果不同,根据效果进行取舍。这是最常用的做法。
利用交叉验证选择模型也是可以的,只是不是最普遍的用法。(选择模型的话 直接简单交叉验证即可,如划分个训练集和测试集)
(2) 一般是从S组结果中选择一个最优的f1,auc对应的模型参数作为选择出的模型参数。
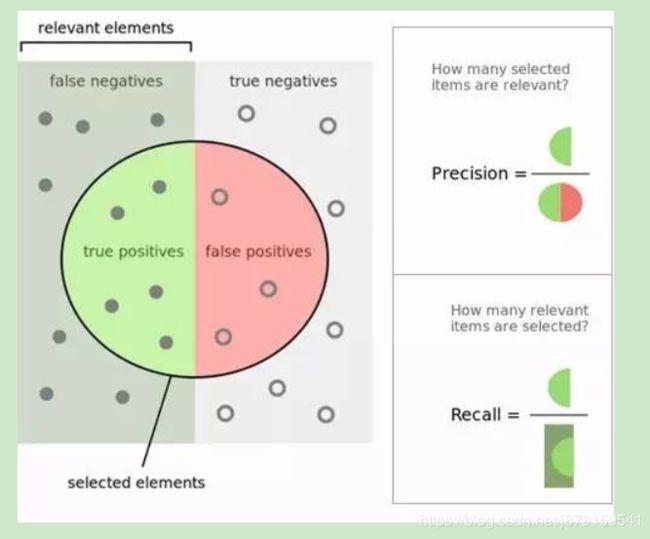
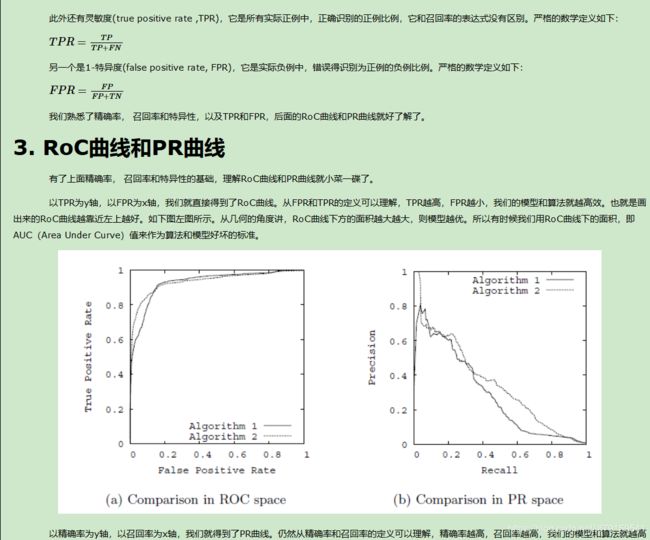
8、Roc曲线与PR曲线
注:TRP又称为真正率,FPR又称为真负率
9、BN
(1)BN遇到relu激活函数如何工作?
(2)为什么需要独立同分布?
我们希望在deep learn中,整个网络中流过的数据都是独立同分布的。
我觉得这事可以从两方面去解释:
一方面我们希望对训练集进行训练后,在测试集上能够发挥很好的性能。那么我们就需要保证训练集和测试集是来自同一个空间,准确来说,是符合同一分布,这对同分布提出了要求。此外,在虽然数据来自同一个空间,但我们并不希望所有数据都聚集在空间中的某一小撮,而是**希望所有数据对于整个空间来说都具有一定代表性,**因此在采样的过程中我们希望是独立得去采样所有的数据。
另一方面,其实是从另一个角度来阐述上一段话,如果数据之间不是同分布的,比如说样本1所有的特征都处于0-1之间,样本2处于10-100,那么网络的参数其实很难去同时迎合两类分布的数据。
独立同分布是BN作者提出的解释,但后面有人反驳了这个解释,请看(3)
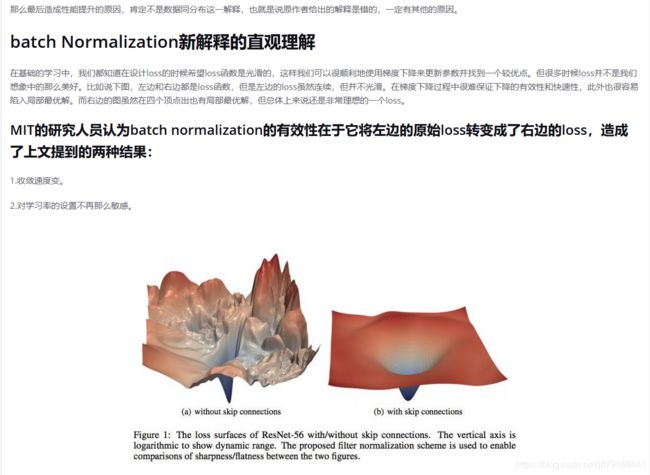
(3)BN的原理的最新解释
BN:收敛速度变快,对学习率的设置不那么敏感
10、线性回归的推广:多项式回归
注:可以将多项式回归转化为线性回归的过程理解为核化的过程。线性回归的这个空间是高维空间,而多项式空间是低维空间。
11、线性模型和树模型的区别
问题:用线性回归和支持向量机回归,在test集上和真实值都有一个稳态误差(稳态时有一个固定偏置),而决策树和随机森林就不会,这是因为什么呢?
答:这个其实反映了线性模型和树模型的区别,线性模型是线性拟合,所以偏差一般不会特别大,总体是中规中矩。而树模型拟合出来的函数是分区段的阶梯函数,这个分区的区间受训练样本分布的影响极大,因此最后的模型误差不是特别稳定,有时特别好,有时特别坏。
12、逻辑回归
(1)逻辑回归中的One vs Rest 与softmax分类器适用场景
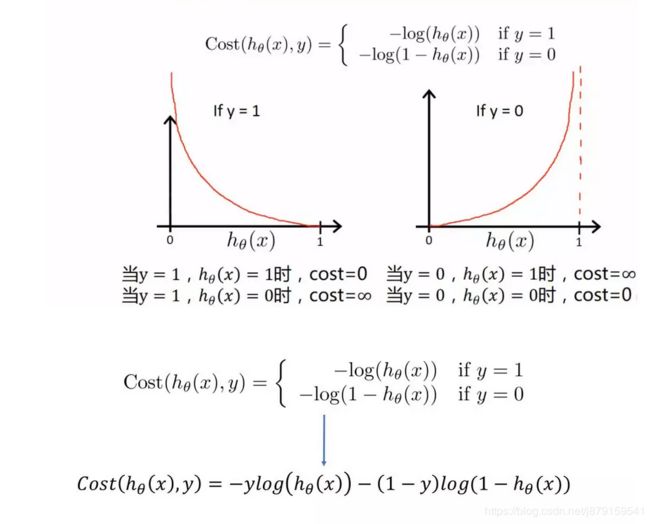
(2)逻辑回归的损失函数、softmax回归的损失函数与交叉熵的损失函数
(3)一个分类算法为什么为叫做逻辑回归?
(4)逻辑回归训练和测试时候的特征预处理的不一致性
(5)逻辑回归的损失函数可视化
13、感知机模型
(1)模型定义
(2)损失函数
(3)需要注意的两个点
(1)感知机算法用点到平面的距离作为损失函数,稍微修改下就和支持向量机一样。
(2)感知机算法可以写成对偶形式,所以也能通过核函数实现非线性分类。
下面是感知机的对偶形式:
(4)感知机模型与逻辑回归的异同点
参考:这篇文章的末尾
14、频率学派与贝叶斯学派对概率定义的不同
(1)频率学派
事件A发生的概率是常数。
事件A发生的概率是重复多次进行同一实验得到的。
(2)贝叶斯学派
事件A发生的概率是变化的,并非常数。
事件A发生的概率是特定数据集下的条件概率。
事件A发生的概率是后验概率,且事件A发生的先验概率已给定。
频率学派认为模型是一成不变的,贝叶斯学派认为模型是随着数据的更新而不断更新,频率学派和贝叶斯学派都可以使用最大似然函数来估计模型。
**贝叶斯思想:**贝叶斯是主观评价事件发生的概率,根据先验知识来假设先验分布,若观测的数据符合先验分布,则后验分布与先验分布类似;若观测的数据不符合先验分布,则后验分布开始向观测数据倾斜,若观测数据为无穷大时,那么前验分布可以忽略不计,最大似然函数估计参数与后验分布估计参数相同,直接可以用最大似然函数来估计参数。
15、为什么选择β分布作为先验分布
(1)β分布的定义
(2)β分布作为先验分布的原因
因为β分布是概率分布的分布,α,β取不同的值,可以形成不同的先验分布
如,α=1,β=1,β分布符合均匀分布,即参数空间所有取值的概率相等;假设参数的先验分布是高斯分布,设置参数α和β相等(α>1)使β分布成为高斯分布,α越大方差越小。
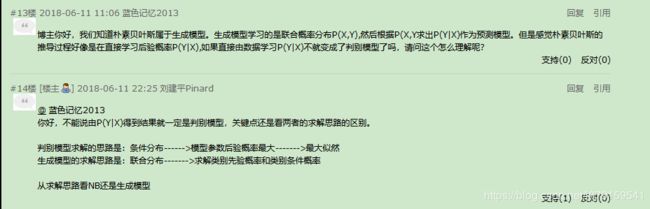
16、分类问题中的判别式模型和生成性模型
我们常把分类问题分成两个阶段:推断阶段和决策阶段,对于输入变量x,分类标记为Ck。推断阶段和决策阶段具体表示为:
推断阶段:估计P(x,Ck)的联合概率分布,对P(x,Ck)归一化,求得后验概率P(Ck|x)。
**决策阶段:**对于新输入的x,可根据后验概率P(Ck|x)得到分类结果。
判别式模型和生成性模型的区别:
**判别式模型:**简单的学习一个函数,将输入x直接映射为决策,称该函数为判别式函数。
如最小平方法,Fisher线性判别法和感知器法。
**生成式模型:**推断阶段确定后验概率分布,决策阶段输出分类结果,生成式模型包含两个阶段。
如logistic回归模型。
17、KNN
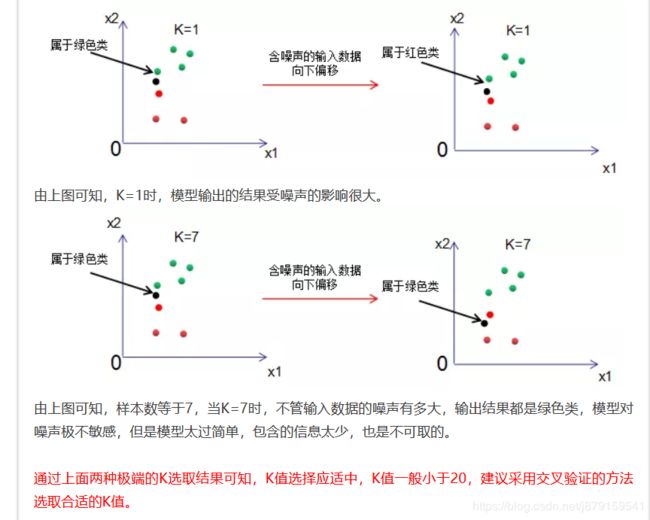
(1)K值的选择
K取值较小时,模型复杂度高,训练误差会减小,泛化能力减弱;K取值较大时,模型复杂度低,训练误差会增大,泛化能力有一定的提高。
KNN模型的复杂度可以通过对噪声的容忍度来理解,若模型对噪声很敏感,则模型的复杂度高;反之,模型的复杂度低。为了更好理解模型复杂度的含义,我们取一个极端,分析K=1和K="样本数"的模型复杂度。
(2)KD树的搜索过程还不太理解
参考:
(3)KNN算法的优缺点
优点:
1)算法简单,理论成熟,可用于分类和回归。
2)对异常值不敏感。
3)可用于非线性分类。
4)比较适用于容量较大的训练数据,容量较小的训练数据则很容易出现误分类情况。
5)KNN算法原理是根据邻域的K个样本来确定输出类别,因此对于不同类的样本集有交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为合适。
缺点:
1)时间复杂度和空间复杂度高。
2)训练样本不平衡,对稀有类别的预测准确率低。
3)相比决策树模型,KNN模型可解释性不强。
参考:这个优缺点总结的更全面
(4)数据是否为线性可分的以及如何选择不同的模型
18、SVM
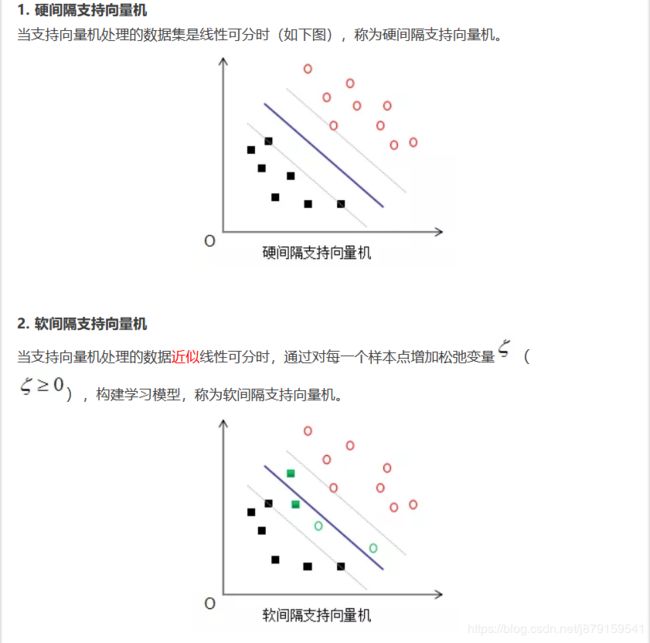
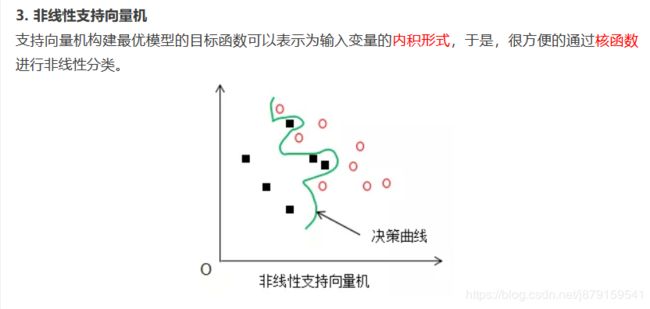
(1)支持向量机种类
我们在工作或学习中遇到的训练数据集常分为三种,线性可分数据集,近似线性可分数据集和非线性可分数据集,对应的支持向量机算法分别为线性可分支持向量机( 硬间隔支持向量机),线性支持向量机( 软间隔支持向量机)和非线性支持向量机。
(2)SVM从零开始推导公式
参考1 参考2
(3)SVM的思想起源
在感知机模型中,我们可以找到多个可以分类的超平面将数据分开,并且优化时希望所有的点都被准确分类。但是实际上离超平面很远的点已经被正确分类,它对超平面的位置没有影响。我们最关心是那些离超平面很近的点,这些点很容易被误分类。如果我们可以让离超平面比较近的点尽可能的远离超平面,最大化几何间隔,那么我们的分类效果会更好一些。SVM的思想起源正起于此。
(4)软间隔时的a的取值范围
(5)软间隔和硬间隔时的b是否唯一
(6)软间隔最大化时样本点位置的判断
(7)核函数的意义
我们遇到线性不可分的样例时,常用做法是把样例特征映射到高维空间中去(如上一节的多项式回归)但是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到令人恐怖的。此时,核函数就体现出它的价值了,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数好在它在低维上进行计算,而将实质上的分类效果(利用了内积)表现在了高维上,这样避免了直接在高维空间中的复杂计算,真正解决了SVM线性不可分的问题。
(8)Ei的更新过程
(9)SVC与SVR的区别
(10)SVM里的C
(11)SVC与SVR通过合页损失函数进行统一
(12)
19、决策树
(1)图示ID3决策树算法流程
由于刘建平老师的关于决策树这块没有图示,理解起来有些费劲,因此这块结合八哥笔记一起食用比较好
参考
(2)以信息增益作为评价标准偏向于选择较多的特征
对于信息增益作为评价标准偏向于选择较多的特征,其实是很简单的。从信息增益的定义我们知道,它度量了输出在知道特征以后不确定性减少程度。
当特征类别数较多时候,这个不确定性减少程度一般会多一些,因为此时特征类别数较多,每个类别里的样本数量较少,样本更容易被划分的散落到各个特征类别,即样本不确定性变小。
当然,这个说法是针对大多数情况的。某一些极端的样本分布,有可能特征类别少的反而可能信息增益大。
(3)决策树C4.5中的连续特征离散化
(4)CART回归树和CART分类树的建立和预测的区别
(5)决策树不用对特征做标准化预处理
(6)决策树如何并行计算
其实决策树在决策分支选择出来之前,肯定是不能提前并行计算子分支的决策的。
所以唯一的并行就是并行的选择划分特征和特征的划分点。比如我们在决策树某节点有N个特征需要选择,那么我们可以开N个线程去并行计算每个特征的最优划分点的基尼系数,最后汇总,看谁的基尼系数小。那么这个特征的最优划分点被用来建立子分支。
(7)CART决策树进行剪枝的小疑问
20、贝叶斯算法
(1)既然朴素贝叶斯对输入数据的独立性有要求,那么是不是可以先PCA一下
(2)条件概率分布与条件概率分布的某一个概率值
(3)通俗例子讲解朴素贝叶斯求解过程
参考
(4)
21、最大熵模型
(1)算法流程的简单理解
(2)逻辑回归与最大熵
线性链条件随机场是逻辑回归的序列化版本,逻辑回归又是广义线性模型的范畴,广义线性模型是不是也是通过熵理论来建模推导出来的呢?就是说,熵理论是假设性约束性最弱的一个理论,通过它可以推导出最一般化的模型,
其实所有分类回归算法模型都可以从熵理论的角度来解释为什么这样优化。
但是直接使用熵理论优化,不是很方便,所以才演进出这么多不同的分类回归算法
逻辑回归与最大熵的相似处:
(3)机器学习面试之最大熵模型(通俗易懂)
参考
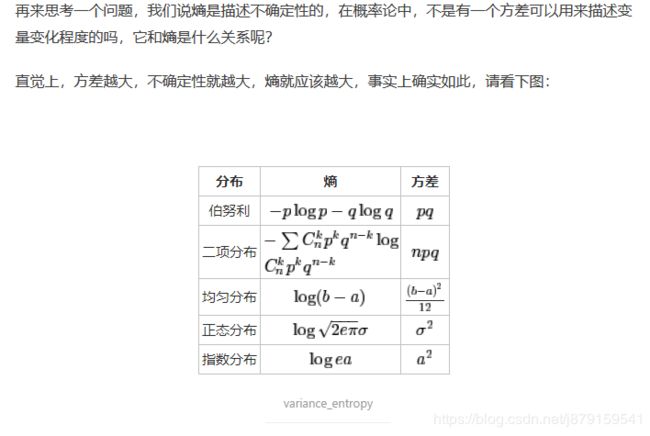
(4)方差与熵的关系
(5)各种熵之间的关系
![]()
互熵(KL散度、相对熵)、交叉熵、条件熵、联合熵:参考
(6)
22、集成学习概述
(1)结合策略之stacking(学习法)
(2)集成学习防止过拟合
boosting算法一般是一步步的去拟合目标,这样比起一次尝试拟合训练集有更大泛化能力。bagging算法则由于使用了多次的自采样,这样增加模型泛化能力。
(3)样本权重如何处理
样本权重会对弱学习器的误分类计算由影响。如果误分类的样本权重大,则损失会更大。也就是在优化损失函数的时候考虑样本权重,一般是乘以权重后再进行训练。
比如Adaboost如果你使用CART回归树做弱学习器,那么在分裂子树的时候,计算均方误差时,所有的 样本特征都要乘以自己权重后再参与计算。
(4)
23、GBDT
(1)adaboost和GBDT的不同
adaboost和GBDT不一样的地方最明显的就是损失函数那里了**,adaboost的目标是找到一个可以使当前损失函数最小的弱分类器,具体的数学解是偏导数等于零的解,关于这个说法可以看一下李航的统计学习方法。而GBDT不同的地方是说**让偏导数等于零这个解不是对所有的损失函数有效的,在adaboost里面做分类的时候,指数函数做损失函数,这个解是可求的,但是换成一般函数怎么办呢?然后就在损失函数ft-1(x)那里做一阶泰勒展开,容易做了,因为展开后的方城变成了一个常数加上一阶梯度和新的弱分类器的乘积,所以梯度和弱分类器的乘积越小,损失函数就越小,所以要拿逆梯度来拟合新的弱分类器,这时候可以把弱分类器分类作为步长,让损失函数沿着梯度在做逆梯度下降。这应该是典型的不同的地方吧。至于一些正则项的存在很大程度是为了限制步长和弱分类器的复杂度,限制弱分类器的复杂度就不用说了,限制步长就是因为在逆梯度方向一步不能迈的太大。
(2)随机森林与GBDT对异常点的处理
GBDT不止可以使用健壮的损失函数来减少异常点一些。使用到的方法还有:1)通过正则化来减少异常点影响。2)通过无放回子采样来减少异常点影响。
对于异常点的鲁棒性,随机森林要比GBDT好的多。
主要原因是GBDT的模型在迭代过程中较远的异常点残差往往会比正常点大,导致最终建立的模型的出现偏差。
一般我(这里指刘建平大佬)的经验是,异常点少的样本集GBDT表现更加优秀,而异常点多的样本集,随机森林表现更好。
(3)对数损失函数是如何度量损失的?
参考 黑白无常 的回答