python 整型无限大问题

python 整型无限大问题

python里，整数的范围是无限大
实际范围受限于运行时的内存大小

参考C/C++，int不管是32、64、128都是有明确的范围大小的。
因为CPU内部的数字是二进制，用一定的位长的表示一个数
比如8位的无符号整型:
能表示的最大的数就是 1111 1111 =>1 0000 0000 - 1=> 2^9 - 1 = 511

那么这样计算机里的数轴就不是日常认知里的一条直线，而是一个曲线组成的闭合图形，比如圆，好像时钟一样。数轴能表示的的范围由 CPU内部位数 以及 编译器决定。

回到python的问题

为什么python可以实现无限大的数？

• 事实：python理论上有无限大的数，实际情况下会受运行的电脑内存限制
• 猜测：可能是用的 高精度算法 + 动态分配数组大小。

那么我想证明一下这个假设。

如果是使用的动态分配，那么，数字越大(主要是位数越多)，重新分配内存的次数就会越频繁，额外开销就越大（计算之外花费的时间），也就是时间会更多。

这里我运行一个程序:
计算 3 ^ i ，记录每次计算花费的时间，计算过程用的快速幂

import time
import matplotlib.pyplot as plt


def quick_pow(a, b):
    # 快速求幂 return a^b
    if b == 0:
        return 1
    ans = 1
    while b != 0:
        if b & 1:
            ans *= a
        b >>= 1
        a *= a
    return ans


if __name__ == '__main__':
    y = []
    x = []
    i = 1
    while i < 100000000:
        print(i)
        x.append(i)
        begin_time = time.time()	#	记录开始时间
        quick_pow(3, i)				#	计算 3^i
        end_time = time.time()		#	记录结束时间
        i *= 2
        y.append(end_time - begin_time)

    print("求3^i 花费时间")
    print("指数(i):\n", x)
    print("时间(t):\n", y)
    plt.plot(x, y)
    plt.show()

运行结果如图

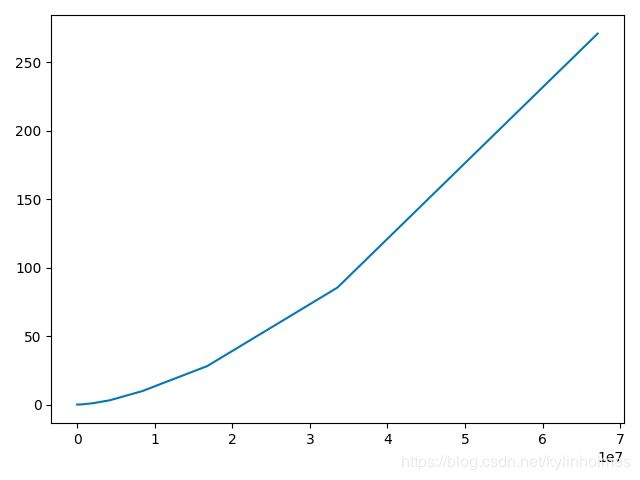
可以看到结果和预期的一样，曲线不是线性的，随着计算数字的增大，斜率也在增加。另外，这样动态分配的方式会受限于内存大小，和上面的描述也一致

结论
我觉得可以说，python无限大整型的实现就是高精+动态分配

后来更新的：
因为到最后几次数据由于 i 的值过大，2^i 跨越区间太大，数据不明显，所以
之后我做了细分：
发现图片是这样的，中间就是有几处莫名其妙的波动、突变，做几次都是这样


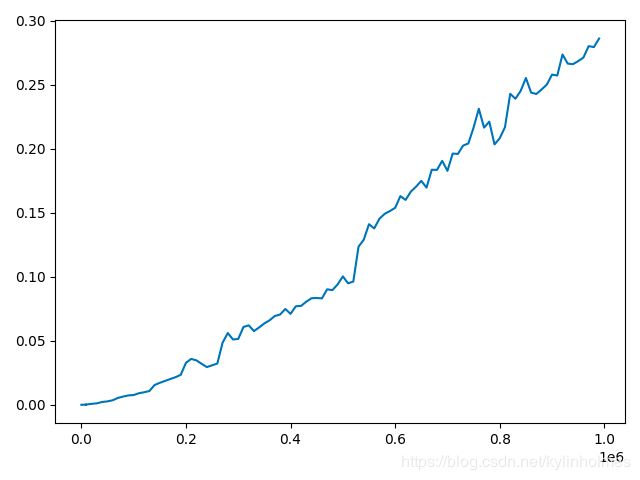
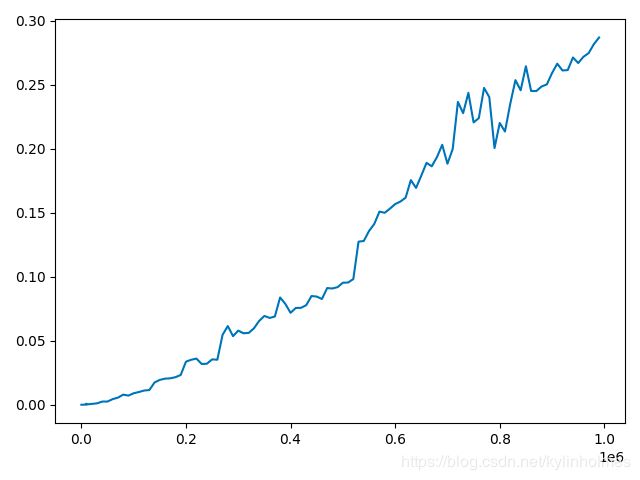
这里我圈出了几个一直出现的异常点

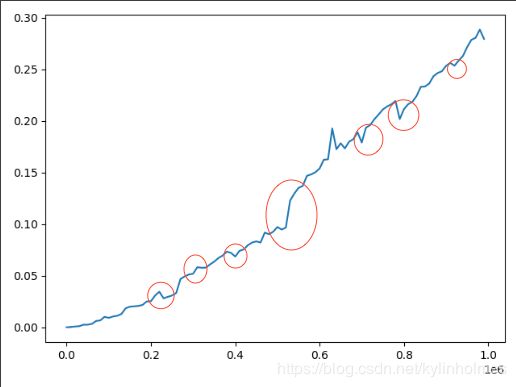
出现这种情况我还没有想到很好的解释，想不到为什么时间反而会减小

这样情况我有想到一种可能的原因，等我之后更新

因为有朋友评论了，正好提醒了我，后面说到的这个原因我还没解释。
当然只是我一种猜想，这里简单的解释一下。

我的猜想： 是快速幂的问题

比如对于一个指数i，求$3^i$

我们需要将i转换成2进制数。这里我们假设一种极端情况
我们的指数是100000000000001实际情况只会更大
那么，快速幂的时候，只会算最前面的一个1和最后面的一个1。
相当于这个指数$2^{15}+1$ 只计算2次 忽略 a*=a 的运算

如果恰好，上一次运算，指数是111111100000001，就需要计算8次。

综上，极有可能，出现 下一次运算时间 比上一次少的情况，也就是所谓的 “异常点” 。

• 在这样的假设下，又因为每次运行时的 i 是确定的，所以出现 “异常点” 的位置也是可以确定的，相对关系也是不会因为运算时计算机状态改变。