时间复杂度-线性对数时间nlogn的一些研究

排序算法的时间复杂度

时间复杂度的本质就是一个函数f(x)=y，其中y是时间，x是被操作的元素数量，分析的是随着x元素的增加，计算机所需计算时间y的变化。时间复杂度的写法是$O(x)$，x是元素数量，O返回的是时间，时间复杂度不会追求计算机完成该算法的精确时间，也没办法计算，例如计算机对于不同的数据类型例如float或int所需的计算时间肯定是不同的，所以O()只是对一种xy线性关系粗糙的描述。

绝大部分的排序算法的平均时间复杂度就是两种，慢的$O(n^2)$或是快的$O(n\ast lo{g}_2^n)$。$O(n^2)$数学的名字叫quadratic time平方时间 ，从代码的角度看就是两个for循环，比如说$n=5^2=25$，那么两个五次for循环正好是25次循环，下面要研究的是$O(n\ast lo{g}_2^n)$，linearithmic time线性对数时间。

二叉树与$nlo{g}_2^n$

假设n为一个2的倍数，它可以以二叉树的形式不断向下二分，设这个树的深度为k，可以看出每一层的节点内的数的和都是n，那么整个树所有节点的合为n*k

[图1]
从上图中可以看出每个节点内的数量还可以用$\frac{1}{2^a}\ast n$来表示，观察最底层可得出:
$1=\frac{1}{2^{k-1}}\ast n$
既是
$2^{k-1}=n$
根据对数公式：
$k-1=lo{g}_2^n$
$k=lo{g}_2^n+1$
已知$sum=n\ast k$所以：
$sum=n\ast (lo{g}_2^n+1)=nlo{g}_2^n+n$
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，当用二分法进行问题分解时，这里$nlo{g}_2^n$可以代表在最完美的二分情况下的各个子问题的和。代入进$O(nlo{g}_2^n+n)$，最后的n按O()约定可以当常数约掉（另外很多算法里当问题的规模只有1时计算就已经结束了，$O(nlo{g}_2^n)$反而更加精准）。下面分析一个具体的nlogn算法。

快速排序的大致复杂度分析

本文分析的案例是快速排序，快排根据如何对数组进行划分再次递归有一些不同的版本，在一些case上的复杂度会有些区别，以下是称为Hoare分区法的C#版本
C#代码：

    void Quicksort(int[] arr, int low, int high)
    {
        if (low < high)
        {
            int pivot = arr[(low + high) / 2];
            int left = low - 1;
            int right = high + 1;

            while (true)
            {
                do
                {
                    left++;
                } while (arr[left] < pivot);

                do
                {
                    right--;
                } while (arr[right] > pivot);

                if (left >= right)
                {
                    pivot = right;
                    break;
                }
                //交换
                int leftCopy = arr[left];
                arr[left] = arr[right];
                arr[right] = leftCopy;
            }
            Quicksort(arr, low, pivot);
            Quicksort(arr, pivot + 1, high);
        }
    }

参数arr是被处理的数组，low是0，high是arr.length-1，从代码可以看出只要输入元素大于两个，那么Quicksort就会进行递归，Sort函数返回的pi可以看做是一个锚点，它将arr划分为两个部分，交给Quicksort分别处理，如果将Sort的递归调用画为一个二叉树，pi就决定了二叉树的分叉情况

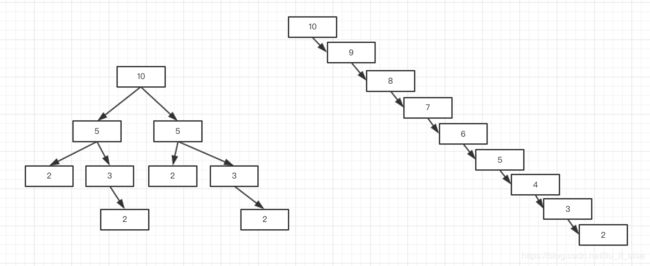
（图1：将Sort递归调用次数画为二叉树）

上图假设arr的长度为10，每个节点代表一次Quicksort调用，节点内数字代表当前函数调用需要处理的数组元素数量，当元素等于1时不会调用。上文已经分析越是完美二分的二叉树，它的深度越接近logn+1，由于这里把1的叶子节点删除了，所以这里的深度k变为了logn。左面的二叉树高度非常接近$lo{g}_2^{10}=3.32$。从上图可以看出越是一个平衡的二叉树它需要处理的元素越少，右边那种极端非平衡的树需要处理的元素总数是最多的。但是该算法的复杂度不只和Quicksort函数的调用次数有关，更主要的是函数内部的操作数量，实际的复杂度还要具体分析。但是上图还是可以反映出一个一般趋势，既是良好平衡的划分有助于降低复杂度。

进一步的复杂度分析

最坏情况worst case

Quicksort函数最主要的操作是数组遍历与数组交换，left与right从arr数组两边向中央移动遍历直到相交，在移动过程中如果发现有需要交换的数就进行交换，当left与right相交后则返回right作为pi锚点将数组一分为二进行递归。

每次数组元素交换行为都会导致right向左移动一位，如果说图1右方的二叉树是最坏情况，那么对于1个长度为10的arr，它的具体行为就是：
left左移10次
right右移1次
交换1次
交换有三行代码，总操作次数为10+1+3=14。
但是考虑一个10个相同数的数组：
left左移5
right右移6次
交换5次
5+6+5*3=26次操作。由于等值数组的二分是完全平衡的，n的大小与交换次数成等比例关系，在n>100时，全等数组就是该算法的worst case。（实测当n不是很大的时候，有些特殊形式的数组操作数量会超过全等值数组例如aaaabaaaab,a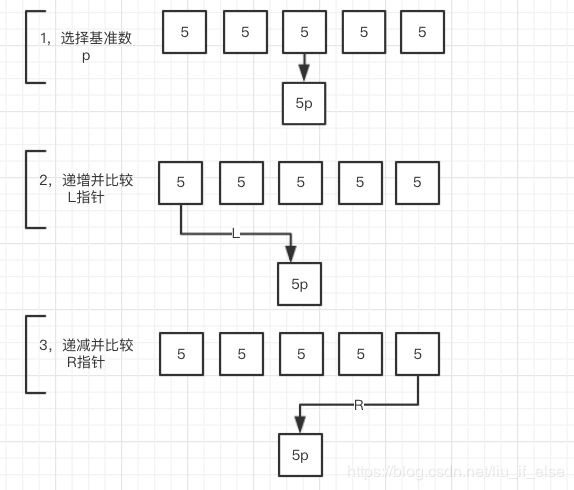
（图2：Quciksort处理等值数组时的具体行为）

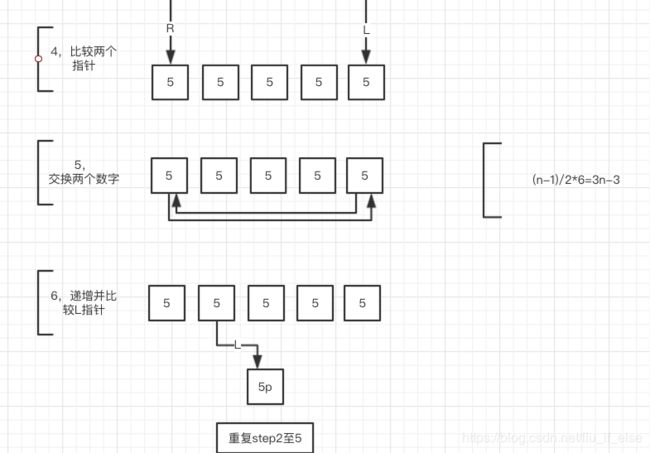
（图3：Quciksort处理等值数组时的具体行为）

（图4：Quciksort处理等值数组时的具体行为）

最佳情况best case

从上文已知交换次数会导致复杂度上升，平衡二分会导致复杂度下降。那么一个不需要交换的平衡二叉树既是best case。它就是一个已经排好序的数组，例如1，2，3，4，5，6，7，8，9，10。不需要任何交换并且每次都是在中央二分。

用表达式计算更加精确的复杂度

分析

首先要更加仔细的剖析代码，给各个操作划分case计数。
Unity测试脚本：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class QuickSortBlog : MonoBehaviour {
    //计数器
    struct counter
    {
        public int operations;   //操作计数
        public int qsCalls;      //Quicksort方法调用次数
        public int qsValidCalls; //有效的Quicksort方法调用次数（操作数大于2）
        public int swapCount;    //交换次数
        public int moveCount;    //移动次数
    };

    counter c;
    counter randomMaxC;
    int[] randomMaxArr;

	// Use this for initialization
	void Start () {
        c=new counter();
        c.operations = 0;
        c.qsCalls = 0;
        c.qsValidCalls = 0;
        c.swapCount = 0;
        c.moveCount = 0;
        int[] arr = new int[10] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
        Quicksort(arr, 0, 9);
        Debug.Log("successive numbers,operations:" + c.operations + ",qsCalls:" + c.qsCalls + ",qsValidCalls:" + c.qsValidCalls + ",swapCount:" + c.swapCount+",moveCount:"+c.moveCount);

        c.operations = 0;
        c.qsCalls = 0;
        c.qsValidCalls = 0;
        c.swapCount = 0;
        c.moveCount = 0;
        arr = new int[10] { 8, 8, 8, 8, 8, 8, 8, 8, 8, 8};
        Quicksort(arr, 0, 9);
        Debug.Log("same numbers,operations:" + c.operations + ",qsCalls:" + c.qsCalls + ",qsValidCalls:" + c.qsValidCalls + ",swapCount:" + c.swapCount + ",moveCount:" + c.moveCount);

        /*Quicksort处理aaaabaaaab形式数组有更差的性能表现
        c.total = 0;
        c.qsCall = 0;
        c.validQSCall = 0;
        c.swapCall = 0;
        c.move = 0;
        temp = new int[10] { 6,6,6,6,8,6,6,6,6,8 };
        Quicksort(temp, 0, 9);
        Debug.Log("aaaabaaaab,numbers:" + c.operations + ",qsCalls:" + c.qsCalls + ",qsValidCalls:" + c.qsValidCalls + ",swapCount:" + c.swapCount + ",moveCount:" + c.moveCount);
        */

        //10000次随机测试
        randomMaxC = new counter();
        randomMaxC.operations = 0;
        randomMaxC.qsCalls = 0;
        randomMaxC.qsValidCalls = 0;
        randomMaxC.swapCount = 0;
        randomMaxC.moveCount = 0;
        for (int i = 0; i < 100000;i++){
            RandomDebug();
        }
        Debug.Log("random numbers,operations:" + randomMaxC.operations + ",qsCalls:" + randomMaxC.qsCalls + ",qsValidCalls:" + randomMaxC.qsValidCalls + ",swapCount:" + randomMaxC.swapCount+ ",moveCount:" + randomMaxC.moveCount);
        for (int i = 0; i < 10; i++)
        {
            Debug.Log(randomMaxArr[i].ToString());
        }
    }
    //随机数组生成与测试
    void RandomDebug(){
        c.operations = 0;
        c.qsCalls = 0;
        c.qsValidCalls = 0;
        c.swapCount = 0;
        c.moveCount = 0;
        int[] debugArray = new int[10];
        int[] copyArray = new int[10];
        for (int i = 0; i < 10;i++){
            debugArray[i] = Random.Range(1, 11);
            copyArray[i] = debugArray[i];
        }
        Quicksort(debugArray, 0, 9);
        SelectRandomMax(copyArray);
    }
    //worst case筛选
    void SelectRandomMax(int[] arr){
        if(c.operations>randomMaxC.operations){
            randomMaxArr = arr;

            randomMaxC.operations = c.operations;
            randomMaxC.qsCalls = c.qsCalls;
            randomMaxC.qsValidCalls = c.qsValidCalls;
            randomMaxC.swapCount = c.swapCount;
            randomMaxC.moveCount = c.moveCount;
        }
    }

    void Quicksort(int[] arr, int low, int high)
    {
        c.qsCalls++;
        c.operations++;
        if (low < high)
        {
            c.qsValidCalls++;
            int pivot = arr[(low + high) / 2];
            int left = low - 1;
            int right = high + 1;
            c.operations+=3;

            while (true)
            {
                do
                {
                    left++;
                    c.operations++;
                    c.moveCount++;
                } while (arr[left] < pivot);

                do
                {
                    right--;
                    c.operations++;
                    c.moveCount++;
                } while (arr[right] > pivot);

                if (left >= right)
                {
                    pivot = right;
                    c.operations += 2;
                    break;
                }
                c.swapCount++;
                c.operations++;
                //交换
                int leftCopy = arr[left];
                arr[left] = arr[right];
                arr[right] = leftCopy;
                c.operations+=3;
            }
            Quicksort(arr, low, pivot);
            Quicksort(arr, pivot + 1, high);
            c.operations+=2;
        }
    }
}

结合上面代码与图1可以归纳出以下几点，当arr长度为n时：
worst case最差情况：
1，有效调用(arr长度大于2)Quicksort方法n-1次。每次调用与之相关的操作有8次。
2，无效调用Quicksort方法n次。每次调用与之相关的操作有1次。
3，问题分治的二叉树高度基本等于logn。
4，在二叉树每一层，数组元素交换相关操作次数根据奇偶数case平均后等于n+1.5。
5，在二叉树每一层，数组遍历相关操作次数根据奇偶数case平均后等于(n/2+0.25)*4。

best case最佳情况：
1，2，3，5同上。第4条数组元素交换次数为0。

结合以上情况可得出表达式：
worst case:
$f(n)=(n-1)\ast 8+n+lo{g}_2^n\ast ((\frac{n}{2}+0.25)\ast 4+(n+1.5))$
best case:
$f(n)=(n-1)\ast 8+n+lo{g}_2^n\ast (n+1.5)$

测试

1，n=10
最佳情况，连续数字
Unity脚本：operations=125
表达式计算结果：f(n)=120.2

最差情况，相同数字
Unity脚本：operations=190
表达式计算结果：f(n)=189.96

2,n=100
最佳情况，连续数字
Unity脚本：operations=1663
表达式计算结果：f(n)=1566.35

最差情况，相同数字
Unity脚本：operations=2986
表达式计算结果：f(n)=2901.7

3,n=1000
最佳情况，连续数字
Unity脚本：operations=19967
表达式计算结果：f(n)=18972.3

最差情况，相同数字
Unity脚本：operations=40582
表达式计算结果：f(n)=38914.27

表达式计算出的值与真实数字还是有一些误差，主要是二叉树深度那块的处理方案还是有问题。

图像

有了表达式就可以画图了。红线是$O(n^2)$，蓝线是$O(nlogn)$，灰色区域是best case和worst case表达式的积分面积，该算法所有case的复杂度都在这范围内

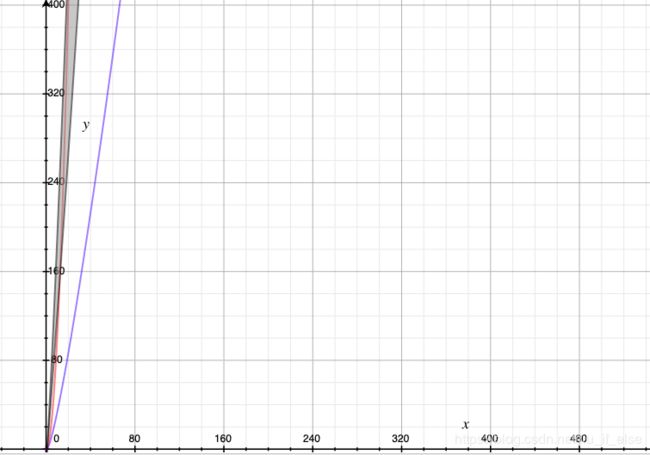
（图5：n<100）

（图5：n<1000）

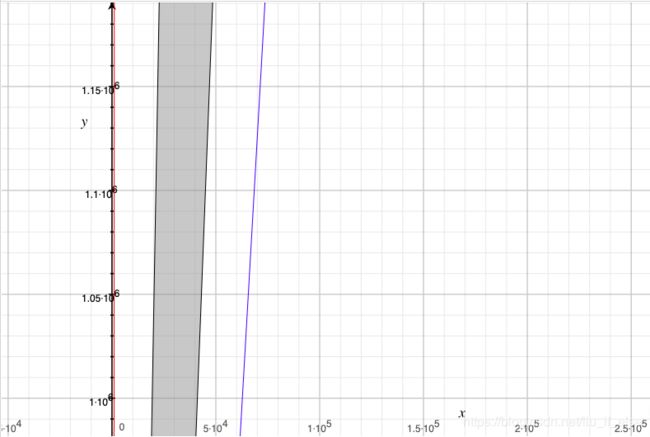
（图5：n<50000）

---

参考：
Quicksort–hoare partition scheme:https://en.wikipedia.org/wiki/Quicksort#Hoare_partition_scheme
时间复杂度 O(log n) 意味着什么？:https://juejin.im/entry/593f56528d6d810058a355f4
A Gentle Introduction to Algorithm Complexity Analysis: https://discrete.gr/complexity/

---

维护日志：
2020-2-5：修改整理