递归函数设计方法学习浅析

学习内容来自课程课件，所以不算原创，不过重新把这些内容整理学习一遍总是好的！！！

递归函数常用方法1、分治法  (又称分割求解法)2、后置递归法 3、回溯法

1.分治法设计思想:

l对于一个输入规模为 n 的函数或问题，用某种方法把输入分割成 k(1≤n)个子集，从而产生 k个相似的子问题；

l分别求解这 k个子问题，得出 k个问题的子解;再用某种方法把它们组合成原来问题的解；

l若子问题还相当大，则可以反复使用分治法，直至最后所分得的子问题足够小，以至可以直接求解为止。

常见的解决问题有：斐波那契数列，汉诺塔问题等

2. 后置递归设计思想

假如某个问题的求解过程可以分成若干步进行，并且当前这一步的解可以直接求得，则先求出当前这一步的解，对于余下的问题，若问题的性质和原问题类似，则又可递归求解。

后置递归算法的典型举例: 删除单链表中所有值为x 的数据元素

分析:

1)单链表是一种顺序结构，必须从第一个结点起，逐个检查每个结点的数据元素;

2) 从另一角度看，链表又是一个递归结构，若 L 是带头结点线性链表 (a1, a2, ¼, an) 的头指针，则  L->next是线性链表

    (a2, ¼, an)的头指针。

  3.  回溯法是一种“穷举搜索”方法。其基本思想为:

①假设问题的解为 n 元组 (x1, x2, …, xn)；

②如果n 元组的部分解为 (x1, x2, …, xi) (i且应满足一定的约束条件；

③对于已求得的部分解 (x1, x2, …, xi) ，若在添加 xi+1 之后仍然满足约束条件，则得到一个新的部分解 (x1, x2, …, xi+1) ；之后继续添加 xi+2并检查之；

4.若找不到一个xi+1满足约束条件，则从当前部分解中删去xi, 回溯到前一个部分解(x1,x2, × × ×,xi-1 ),重新添加那些尚未考察过的xi，并检查之；

5. 如此反复进行，直至求得满足约束条件的问题的解，或者证明问题无解；

设四皇后问题的解为 (x1, x2, x3, x4), 其中:

 xi (i=1,2,3,4) ，约束条件为: 其中任意两个xi 和xj不能位于棋盘的同行、同列及同对角线.

皇后问题回溯算法关键:

搜索策略: 深度优先，依次取 xi=1,2,3,4;

约束条件: xi和xj不位于棋盘的同行、同列及同对角线上；

终止条件: 找到满足条件的x1,x2 x3,x4；即:i=n

回溯条件:  在当前初始条件下无解；无解: 回溯到了起始状态,i=0；

void Trial(int i, int n) {
  // 进入本函数时，在n×n棋盘前i-1行已放置了互不攻
  // 击的i-1个棋子。现从第 i 行起继续为后续棋子选择 
  // 满足约束条件的位置。当求得(i>n)的一个合法布局
  // 时，输出之。i 的初始值为1。
  if(i=0)  无解；
  if (i>n) 输出棋盘的当前布局;                //终止
  else  for (j=1;  j<=n; ++j) {                     //试探策略
      在第 i 行第 j 列放置一个棋子;
      if (当前布局合法) Trial(i+1, n); //约束-递归
      移去第 i 行第 j 列的棋子;          //回溯
  }		
} // Trial 

四、递归注意事项

1.先写出问题求解的递归定义,包括两项内容:

   基本项: 描述一个或几个递归过程的终结状态；

   归纳项: 描述如何从当前状态到下一状态的转换；

2  写递归函数时注意: 

       严格定义函数的功能和接口;

        将每一个递归看成一个简单的操作;

             切忌想得太深太远！

3. 分析递归算法的工具是递归树，从递归树上可以得到递归函数的各种相关信息。

l递归树的深度即为递归函数的递归深度

l递归树上的结点数目恰为函数中的主要操作重复进行的次数；

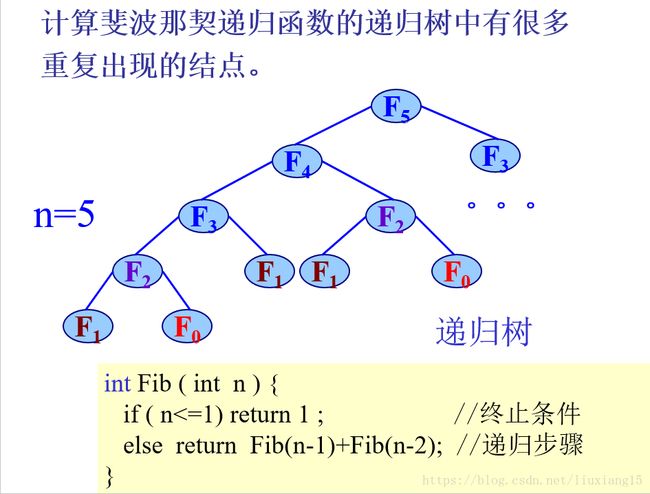
l若递归树蜕化为单支树或者递归树中含有很多相同的结点，则表明该递归函数不适用。比如fib(n) = fib(n-1)+fib(n-2)

在这种情况下会重复计算很多比n小的值得fib值，重复太多！！！

所以这种情况下用迭代会更适合一些！！！