什么是hashtable，如何解决hash冲突

哈希函数：在记录的关键字与记录的存储地址之间建立的一种对应关系叫哈希函数。
哈希函数是一种映象，是从关键字空间到存储地址空间的一种映象。可写成：addr(ai)=H(ki) ，其中i是表中一个元素，addr(ai)是ai的地址， ki是ai的关键字。
哈希表：应用哈希函数，由记录的关键字确定记录在表中的地址，并将记录放入此地址，这样构成的表叫哈希表。
哈希查找(又叫散列查找)：利用哈希函数进行查找的过程叫哈希查找。

冲突处理的方法
1 开放定址法
基本方法：当冲突发生时，形成某个探测序列；按此序列逐个探测散列表中的其他地址，直到找到给定的关键字或一个空地址(开放的地址)为止，将发生冲突的记录放到该地址中。散列地址的计算公式是：
Hi(key)=(H(key)+di) MOD m，i=1, 2, …, k(km-1)
其中：H(key)：哈希函数；m：散列表长度；
di：第i次探测时的增量序列；
Hi(key) ：经第i次探测后得到的散列地址。

⑴ 线性探测法
将散列表T[0 …m-1]看成循环向量。当发生冲突时，从初次发生冲突的位置依次向后探测其他的地址。
增量序列为：di=1, 2, 3, …, m-1
设初次发生冲突的地址是h，则依次探测T[h+1]，T[h+2]…，直到T[m-1]时又循环到表头，再次探测T[0]，T[1]…，直到T[h-1]。探测过程终止的情况是：
◆ 探测到的地址为空：表中没有记录。若是查找则失败；若是插入则将记录写入到该地址；
◆ 探测到的地址有给定的关键字：若是查找则成功；若是插入则失败；
◆ 直到T[h]：仍未探测到空地址或给定的关键字，散列表满。
例1 ：设散列表长为7，记录关键字组为：15, 14, 28, 26, 56, 23，散列函数：H(key)=key MOD 7，冲突处理采用线性探测法。
解：H(15)=15 MOD 7=1 H(14)=14 MOD 7=0
H(28)=28 MOD 7=0 冲突 H1(28)=1 又冲突H2(28)=2 H(26)=26 MOD 7=5
H(56)=56 MOD 7=0 冲突 H1(56)=1 又冲突
H2(56)=2 又冲突 H3(56)=3
H(23)=23 MOD 7=2 冲突 H1(23)=3 又冲突
H3(23)=4

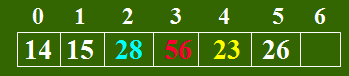
线性探测法的特点
◆ 优点：只要散列表未满，总能找到一个不冲突的散列地址；
◆ 缺点：每个产生冲突的记录被散列到离冲突最近的空地址上，从而又增加了更多的冲突机会(这种现象称为冲突的“聚集”)。
⑵ 二次探测法
增量序列为：di=1²,-1²,2²,-2²,3²,……±k² (k⌊m/2⌋)
上述例题若采用二次探测法进行冲突处理，则：
H(15)=15 MOD 7=1 H(14)=14 MOD 7=0
H(28)=28 MOD 7=0 冲突 H1(28)=1 又冲突
H2(28)=4
H(26)=26 MOD 7=5
H(56)=56 MOD 7=0 冲突 H1(56)=1 又冲突
H2(56)=0 又冲突 H3(56)=4 又冲突 H4(56)=2
H(23)=23 MOD 7=2 冲突 H1(23)=3
二次探测法的特点
◆ 优点：探测序列跳跃式地散列到整个表中，不易产生冲突的“聚集”现象；
◆ 缺点：不能保证探测到散列表的所有地址。

⑶ 伪随机探测法
增量序列使用一个伪随机函数来产生一个落在闭区间[1，m-1]的随机序列。
例2 ： 表长为11的哈希表中已填有关键字为17，60，29的记录，散列函数为H(key)=key MOD 11 。 现有第4个记录，其关键字为38，按三种处理冲突的方法，将它填入表中。
(1) H(38)=38 MOD 11=5 冲突
H1=(5+1) MOD 11=6 冲突
H2=(5+2) MOD 11=7 冲突
H3=(5+3) MOD 11=8 不冲突
(2) H(38)=38 MOD 11=5 冲突
H1=(5+1²) MOD 11=6 冲突
H2=(5-1²) MOD 11=4 不冲突
(3) H(38)=38 MOD 11=5 冲突
设伪随机数序列为9，则H1=(5+9) MOD 11=3 不冲突

3 链地址法（拉链法）
方法：将所有关键字为同义词(散列地址相同)的记录存储在一个单链表中，并用一维数组存放链表的头指针。
设散列表长为m，定义一个一维指针数组：
RecNode *linkhash[m]，其中RecNode是结点类型，每个分量的初值为空。凡散列地址为k的记录都插入到以linkhash[k]为头指针的链表中，插入位置可以在表头或表尾或按关键字排序插入。
例： 已知一组关键字(19, 14, 23, 1, 68, 20, 84, 27, 55, 11, 10, 79) ，哈希函数为：H(key)=key MOD 13，用链地址法处理冲突，如右图图9-17所示 。
优点：不易产生冲突的“聚集”；删除记录也很简单。