台湾国立大学(林轩田)《机器学习技法》(第8讲)Adaptive Boosting (AdaBoost)
课程地址:https://class.coursera.org/ntumlone-001/class
课件讲义:http://download.csdn.net/download/malele4th/10212756
注明:文中图片来自《机器学习技法》课程和部分博客
建议:建议读者学习林轩田老师原课程,本文对原课程有自己的改动和理解
Lecture 8 Adaptive Boosting
翻译:(自适应 提升)
上节课我们主要开始介绍Aggregation Models,目的是将不同的hypothesis得到的gt集合起来,利用集体智慧得到更好的预测模型G。首先我们介绍了Blending,blending是将已存在的所有gt结合起来,可以是uniformly,linearly,或者non-linearly组合形式。然后,我们讨论了在没有那么多gt的情况下,使用bootstrap方式,从已有数据集中得到新的类似的数据集,从而得到不同的gt。这种做法称为bagging。本节课将继续从这些概念出发,介绍一种新的演算法。
目录
- Lecture 8 Adaptive Boosting
- 目录
- Motivation of boosting
- diversity by re-weighting
- Adaptive boosting algorithm
- adaptive boosting in action
- 总结
1 Motivation of boosting
我们先来看一个简单的识别苹果的例子,老师展示20张图片,让6岁孩子们通过观察,判断其中哪些图片的内容是苹果。从判断的过程中推导如何解决二元分类问题的方法。
显然这是一个监督式学习,20张图片包括它的标签都是已知的。首先,学生Michael回答说:所有的苹果应该是圆形的。根据Michael的判断,对应到20张图片中去,大部分苹果能被识别出来,但也有错误。其中错误包括有的苹果不是圆形,而且圆形的水果也不一定是苹果。如下图所示:

上图中蓝色区域的图片代表分类错误。显然,只用“苹果是圆形的”这一个条件不能保证分类效果很好。我们把蓝色区域(分类错误的图片)放大,分类正确的图片缩小,这样在接下来的分类中就会更加注重这些错误样本。
然后,学生Tina观察被放大的错误样本和上一轮被缩小的正确样本,回答说:苹果应该是红色的。根据Tina的判断,得到的结果如下图所示:

上图中蓝色区域的图片一样代表分类错误,即根据这个苹果是红色的条件,使得青苹果和草莓、西红柿都出现了判断错误。那么结果就是把这些分类错误的样本放大化,其它正确的样本缩小化。同样,这样在接下来的分类中就会更加注重这些错误样本。
接着,学生Joey经过观察又说:苹果也可能是绿色的。根据Joey的判断,得到的结果如下图所示:
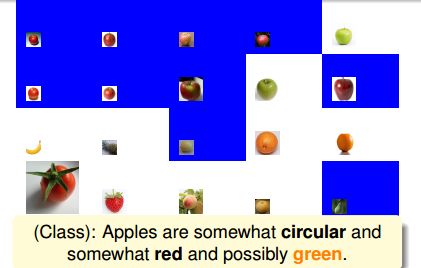
上图中蓝色区域的图片一样代表分类错误,根据苹果是绿色的条件,使得图中蓝色区域都出现了判断错误。同样把这些分类错误的样本放大化,其它正确的样本缩小化,在下一轮判断继续对其修正。
后来,学生Jessica又发现:上面有梗的才是苹果。得到如下结果:

经过这几个同学的推论,苹果被定义为:圆的,红色的,也可能是绿色的,上面有梗。从一个一个的推导过程中,我们似乎得到一个较为准确的苹果的定义。虽然可能不是非常准确,但是要比单一的条件要好得多。也就是说把所有学生对苹果的定义融合起来,最终得到一个比较好的对苹果的总体定义。这种做法就是我们本节课将要讨论的演算法。这些学生代表的就是简单的hypotheses gt,将所有gt融合,得到很好的预测模型G。例如,二维平面上简单的hypotheses(水平线和垂直线),这些简单gt最终组成的较复杂的分类线能够较好地将正负样本完全分开,即得到了好的预测模型。
所以,上个苹果的例子中,不同的学生代表不同的hypotheses gt;最终得到的苹果总体定义就代表hypothesis G;而老师就代表演算法A,指导学生的注意力集中到关键的例子中(错误样本),从而得到更好的苹果定义。其中的数学原理,我们下一部分详细介绍。

2 diversity by re-weighting
参数u相当于是权重因子,当 D^t D ^ t 中第i个样本出现的次数越多的时候,那么对应的 ui u i 越大,表示在error function中对该样本的惩罚越多。所以,从另外一个角度来看bagging,它其实就是通过bootstrap的方式,来得到这些 ui u i 值,作为犯错样本的权重因子,再用base algorithn最小化包含 ui u i 的error function,得到不同的 gt g t 。这个error function被称为bootstrap-weighted error。
这种算法叫做Weightd Base Algorithm,目的就是最小化bootstrap-weighted error。
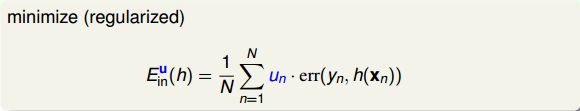


其实这种example-weighted learning,我们在机器学习基石课程第8次笔记中就介绍过class-weighted的思想。二者道理是相通的。
知道了u的概念后,我们知道不同的u组合经过base algorithm得到不同的gt。那么如何选取u,使得到的gt之间有很大的不同呢?之所以要让所有的gt差别很大,是因为上节课aggregation中,我们介绍过gt越不一样,其aggregation的效果越好,即每个人的意见越不相同,越能运用集体的智慧,得到好的预测模型。
为了得到不同的gt,我们先来看看 gt g t 和 gt+1 g t + 1 是怎么得到的:


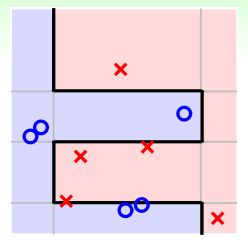
乍看上面这个式子,似乎不好求解。但是,我们对它做一些等价处理,其中分式中分子可以看成gt作用下犯错误的点,而分母可以看成犯错的点和没有犯错误的点的集合,即所有样本点。其中犯错误的点和没有犯错误的点分别用橘色方块和绿色圆圈表示:
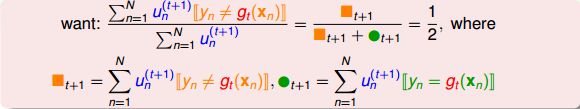


3 Adaptive boosting algorithm




但是,上述步骤还有两个问题没有解决,第一个问题是初始的u(1)应为多少呢?一般来说,为了保证第一次Ein最小的话,设u(1)=1/N即可。这样最开始的g1就能由此推导。第二个问题,最终的G(x)应该怎么求?是将所有的g(t)合并uniform在一起吗?一般来说并不是这样直接uniform求解,因为gt+1是通过gt得来的,二者在Ein上的表现差别比较大。所以,一般是对所有的g(t)进行linear或者non-linear组合来得到G(t)。
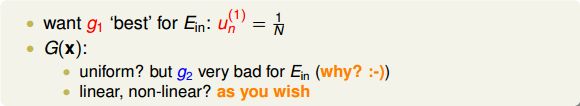
接下来的内容,我们将对上面的第二个问题进行探讨,研究一种算法,将所有的g(t)进行linear组合。方法是计算g(t)的同时,就能计算得到其线性组合系数αt,即aggregate linearly on the fly。这种算法使最终求得gt+1的时候,所有gt的线性组合系数α也求得了,不用再重新计算α了。这种Linear Aggregation on the Fly算法流程为:


这种算法被称为Adaptive Boosting。它由三部分构成:base learning algorithm A,re-weighting factor ⋄t和linear aggregation αt。这三部分分别对应于我们在本节课开始介绍的例子中的Student,Teacher和Class。

综上所述,完整的adaptive boosting(AdaBoost)Algorithm流程如下:

从我们之前介绍过的VC bound角度来看,AdaBoost算法理论上满足:
4 adaptive boosting in action
上一小节我们已经介绍了选择一个“弱弱”的算法A( ϵt≤ϵ<1/2 ϵ t ≤ ϵ < 1 / 2 ,比乱猜好就行),就能经过多次迭代得到Ein=0。我们称这种形式为decision stump(决策残端)模型。下面介绍一个例子,来看看AdaBoost是如何使用decision stump解决实际问题的。
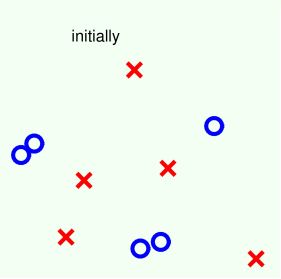
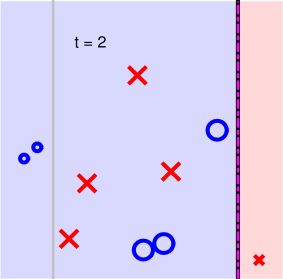
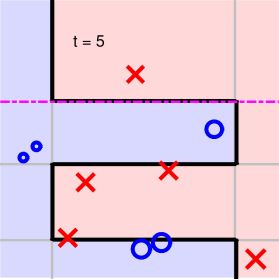
如下图所示,二维平面上分布一些正负样本点,利用decision stump来做切割。
从初始到1~5步



另外一个例子,对于一个相对比较复杂的数据集,如下图所示。它的分界线从视觉上看应该是一个sin波的形式。如果我们再使用AdaBoost算法,通过decision stump来做切割。在迭代切割100次后,得到的分界线如下所示。
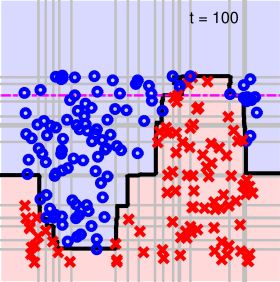
可以看出,AdaBoost-Stump这种非线性模型得到的分界线对正负样本有较好的分离效果。
课程中还介绍了一个AdaBoost-Stump在人脸识别方面的应用:

5 总结
本节课主要介绍了Adaptive Boosting。首先通过讲一个老师教小学生识别苹果的例子,来引入Boosting的思想,即把许多“弱弱”的hypotheses合并起来,变成很强的预测模型。然后重点介绍这种算法如何实现,关键在于每次迭代时,给予样本不同的系数u,宗旨是放大错误样本,缩小正确样本,得到不同的小矩g。并且在每次迭代时根据错误ϵ值的大小,给予不同gt不同的权重。最终由不同的gt进行组合得到整体的预测模型G。实际证明,Adaptive Boosting能够得到有效的预测模型。



