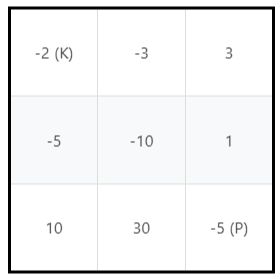
leetcode核心思想:双指针,数字小的那个指针移动classSolution{public:intmaxArea(vector&height){intleft=0;intright=height.size()-1;intmaxArea=0;while(left
leetcode刷题day13|二叉树Part01(递归遍历、迭代遍历、统一迭代、层序遍历)
小冉在学习
leetcode算法职场和发展
递归遍历思路:使用递归的方式比较简单。1、递归函数的传参:因为最后输出一个数组,所以需要传入根节点和一个容器,本来想写数组,但发现长度不能确定,所以选择list。2、终止条件:当访问的节点为空时,return3、递归函数的逻辑:先访问一个节点,递归访问其他节点144.二叉树的前序遍历代码如下:classSolution{publicListpreorderTraversal(TreeNoderoo
leetcode021-合并两个有序链表
陆阳226
问题描述将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。示例:输入:1->2->4,1->3->4输出:1->1->2->3->4->4解答递归法:每一层减去一个较小的节点,直到某个链表为null递归结束。publicstaticListNodesolution(ListNodel1,ListNodel2){if(l1==null){returnl2;}
每日一题《leetcode--LCR 022.环形链表||》
Peace & Love487
题目分享leetcode链表算法笔记数据结构
https://leetcode.cn/problems/c32eOV/我们使用两个指针,fast与slow。它们起始都位于链表的头部。随后slow指针每次向后移动一个位置,而fast指针向后移动两个位置。如果链表中存在环,则fast指针最终将再次与slow指针在环中相遇。structListNode*detectCycle(structListNode*head){structListNode*
LCR 078. 合并 K 个升序链表
装B且挨揍の
LeetCode链表算法数据结构经验分享笔记java
https://leetcode.cn/problems/vvXgSW/description/https://leetcode.cn/problems/vvXgSW/description/解题思路方法一:每个链表维护一个索引,每次找到值最小的节点,索引加一。可以采用优先队列实现。/***Definitionforsingly-linkedlist.*publicclassListNode{*i
LeetCode:2390. 从字符串移除*号 使用栈,时间复杂度O(N)
忍界英雄
每日一题leetcodelinux算法
2390.从字符串移除*号today2390.从字符中移除*号题目表述给你一个包含若干星号*的字符串s。在一步操作中,你可以:选中s中的一个星号。移除星号左侧最近的那个非星号字符,并移除该星号自身。返回移除所有星号之后的字符串。注意:生成的输入保证总是可以执行题面中描述的操作。可以证明结果字符串是唯一的。示例1:输入:s=“leet**cod*e”输出:“lecoe”解释:从左到右执行移除操作:距
⭐算法入门⭐《归并排序》简单01 —— LeetCode 21. 合并两个有序链表
英雄哪里出来
《LeetCode算法全集》算法数据结构链表c++归并排序
饭不食,水不饮,题必须刷C语言免费动漫教程,和我一起打卡!《光天化日学C语言》LeetCode太难?先看简单题!《C语言入门100例》数据结构难?不存在的!《数据结构入门》LeetCode太简单?算法学起来!《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目1、题目描述 将两个不降序链表合并为一个新的不降
【LeetCode 算法笔记】84. 柱状图中最大的矩形
Sardar_
算法leetcode笔记
目录问题描述暴力求解:栈问题描述给定n个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为1。求在该柱状图中,能够勾勒出来的矩形的最大面积。示例1:输入:heights=[2,1,5,6,2,3]输出:10解释:最大的矩形为图中红色区域,面积为10示例2:输入:heights=[2,4]输出:4提示:1int:area=0n=len(heights)foriinrange(n):
【LeetCode 算法笔记】739. 每日温度
Sardar_
算法leetcode笔记
目录问题描述暴力解法栈问题描述给定一个整数数组temperatures,表示每天的温度,返回一个数组answer,其中answer[i]是指对于第i天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用0来代替。示例1:输入:temperatures=[73,74,75,71,69,72,76,73]输出:[1,1,4,2,1,1,0,0]示例2:输入:temperatures=
面试题24. 反转链表
阿星啊阿星
反转链表题目描述定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点示例:输入:1->2->3->4->5->NULL输出:5->4->3->2->1->NULL提示:0<=节点个数<=5000转载来源:力扣(LeetCode)题目分析1→2→3→null初始化时h为1,now为2,h的next设置成null,有:null←1(h) 2(now)→3现在将保存一下now的next
【数据结构和算法实践-树-LeetCode113-路径总和Ⅱ】
NeVeRMoRE_2024
数据结构与算法实践数据结构算法leetcodeb树
数据结构和算法实践-树-LeetCode113-路径总和Ⅱ题目MyThought代码示例JAVA-8题目给你二叉树的根节点root和一个整数目标和targetSum,找出所有从根节点到叶子节点路径总和等于给定目标和的路径。叶子节点是指没有子节点的节点输入:root=[5,4,8,11,null,13,4,7,2,null,null,5,1],targetSum=22输出:[[5,4,11,2],[
单词搜索 II
xialu
来源:力扣(LeetCode)链接:https://leetcode-cn.com/problems/word-search-ii题目描述:给定一个mxn二维字符网格board和一个单词(字符串)列表words,找出所有同时在二维网格和字典中出现的单词。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重
JAVA中的Enum
周凡杨
javaenum枚举
Enum是计算机编程语言中的一种数据类型---枚举类型。 在实际问题中,有些变量的取值被限定在一个有限的范围内。 例如,一个星期内只有七天 我们通常这样实现上面的定义:
public String monday;
public String tuesday;
public String wensday;
public String thursday
赶集网mysql开发36条军规
Bill_chen
mysql业务架构设计mysql调优mysql性能优化
(一)核心军规 (1)不在数据库做运算 cpu计算务必移至业务层; (2)控制单表数据量 int型不超过1000w,含char则不超过500w; 合理分表; 限制单库表数量在300以内; (3)控制列数量 字段少而精,字段数建议在20以内
Shell test命令
daizj
shell字符串test数字文件比较
Shell test命令
Shell中的 test 命令用于检查某个条件是否成立,它可以进行数值、字符和文件三个方面的测试。 数值测试 参数 说明 -eq 等于则为真 -ne 不等于则为真 -gt 大于则为真 -ge 大于等于则为真 -lt 小于则为真 -le 小于等于则为真
实例演示:
num1=100
num2=100if test $[num1]
XFire框架实现WebService(二)
周凡杨
javawebservice
有了XFire框架实现WebService(一),就可以继续开发WebService的简单应用。
Webservice的服务端(WEB工程):
两个java bean类:
Course.java
package cn.com.bean;
public class Course {
private
重绘之画图板
朱辉辉33
画图板
上次博客讲的五子棋重绘比较简单,因为只要在重写系统重绘方法paint()时加入棋盘和棋子的绘制。这次我想说说画图板的重绘。
画图板重绘难在需要重绘的类型很多,比如说里面有矩形,园,直线之类的,所以我们要想办法将里面的图形加入一个队列中,这样在重绘时就
Java的IO流
西蜀石兰
java
刚学Java的IO流时,被各种inputStream流弄的很迷糊,看老罗视频时说想象成插在文件上的一根管道,当初听时觉得自己很明白,可到自己用时,有不知道怎么代码了。。。
每当遇到这种问题时,我习惯性的从头开始理逻辑,会问自己一些很简单的问题,把这些简单的问题想明白了,再看代码时才不会迷糊。
IO流作用是什么?
答:实现对文件的读写,这里的文件是广义的;
Java如何实现程序到文件
No matching PlatformTransactionManager bean found for qualifier 'add' - neither
林鹤霄
java.lang.IllegalStateException: No matching PlatformTransactionManager bean found for qualifier 'add' - neither qualifier match nor bean name match!
网上找了好多的资料没能解决,后来发现:项目中使用的是xml配置的方式配置事务,但是
Row size too large (> 8126). Changing some columns to TEXT or BLOB
aigo
column
原文:http://stackoverflow.com/questions/15585602/change-limit-for-mysql-row-size-too-large
异常信息:
Row size too large (> 8126). Changing some columns to TEXT or BLOB or using ROW_FORMAT=DYNAM
JS 格式化时间
alxw4616
JavaScript
/**
* 格式化时间 2013/6/13 by 半仙
[email protected]
* 需要 pad 函数
* 接收可用的时间值.
* 返回替换时间占位符后的字符串
*
* 时间占位符:年 Y 月 M 日 D 小时 h 分 m 秒 s 重复次数表示占位数
* 如 YYYY 4占4位 YY 占2位<p></p>
* MM DD hh mm
队列的移除一般都是使用的remov();都可以移除的,但是在昨天做线程移除的时候出现了点问题,没有将遍历出来的全部移除, 代码如下;
//
package com.Thread0715.com;
import java.util.ArrayList;
public class Threa
Runnable接口使用实例
bijian1013
javathreadRunnablejava多线程
Runnable接口
a. 该接口只有一个方法:public void run();
b. 实现该接口的类必须覆盖该run方法
c. 实现了Runnable接口的类并不具有任何天
oracle里的extend详解
bijian1013
oracle数据库extend
扩展已知的数组空间,例:
DECLARE
TYPE CourseList IS TABLE OF VARCHAR2(10);
courses CourseList;
BEGIN
-- 初始化数组元素,大小为3
courses := CourseList('Biol 4412 ', 'Psyc 3112 ', 'Anth 3001 ');
--
【httpclient】httpclient发送表单POST请求
bit1129
httpclient
浏览器Form Post请求
浏览器可以通过提交表单的方式向服务器发起POST请求,这种形式的POST请求不同于一般的POST请求
1. 一般的POST请求,将请求数据放置于请求体中,服务器端以二进制流的方式读取数据,HttpServletRequest.getInputStream()。这种方式的请求可以处理任意数据形式的POST请求,比如请求数据是字符串或者是二进制数据
2. Form
【Hive十三】Hive读写Avro格式的数据
bit1129
hive
1. 原始数据
hive> select * from word;
OK
1 MSN
10 QQ
100 Gtalk
1000 Skype
2. 创建avro格式的数据表
hive> CREATE TABLE avro_table(age INT, name STRING)STORE
nginx+lua+redis自动识别封解禁频繁访问IP
ronin47
在站点遇到攻击且无明显攻击特征,造成站点访问慢,nginx不断返回502等错误时,可利用nginx+lua+redis实现在指定的时间段 内,若单IP的请求量达到指定的数量后对该IP进行封禁,nginx返回403禁止访问。利用redis的expire命令设置封禁IP的过期时间达到在 指定的封禁时间后实行自动解封的目的。
一、安装环境:
CentOS x64 release 6.4(Fin
java-二叉树的遍历-先序、中序、后序(递归和非递归)、层次遍历
bylijinnan
java
import java.util.LinkedList;
import java.util.List;
import java.util.Stack;
public class BinTreeTraverse {
//private int[] array={ 1, 2, 3, 4, 5, 6, 7, 8, 9 };
private int[] array={ 10,6,
Spring源码学习-XML 配置方式的IoC容器启动过程分析
bylijinnan
javaspringIOC
以FileSystemXmlApplicationContext为例,把Spring IoC容器的初始化流程走一遍:
ApplicationContext context = new FileSystemXmlApplicationContext
("C:/Users/ZARA/workspace/HelloSpring/src/Beans.xml&q
[科研与项目]民营企业请慎重参与军事科技工程
comsci
企业
军事科研工程和项目 并非要用最先进,最时髦的技术,而是要做到“万无一失”
而民营科技企业在搞科技创新工程的时候,往往考虑的是技术的先进性,而对先进技术带来的风险考虑得不够,在今天提倡军民融合发展的大环境下,这种“万无一失”和“时髦性”的矛盾会日益凸显。。。。。。所以请大家在参与任何重大的军事和政府项目之前,对
spring 定时器-两种方式
cuityang
springquartz定时器
方式一:
间隔一定时间 运行
<bean id="updateSessionIdTask" class="com.yang.iprms.common.UpdateSessionTask" autowire="byName" />
<bean id="updateSessionIdSchedule
简述一下关于BroadView站点的相关设计
damoqiongqiu
view
终于弄上线了,累趴,戳这里http://www.broadview.com.cn
简述一下相关的技术点
前端:jQuery+BootStrap3.2+HandleBars,全站Ajax(貌似对SEO的影响很大啊!怎么破?),用Grunt对全部JS做了压缩处理,对部分JS和CSS做了合并(模块间存在很多依赖,全部合并比较繁琐,待完善)。
后端:U
运维 PHP问题汇总
dcj3sjt126com
windows2003
1、Dede(织梦)发表文章时,内容自动添加关键字显示空白页
解决方法:
后台>系统>系统基本参数>核心设置>关键字替换(是/否),这里选择“是”。
后台>系统>系统基本参数>其他选项>自动提取关键字,这里选择“是”。
2、解决PHP168超级管理员上传图片提示你的空间不足
网站是用PHP168做的,反映使用管理员在后台无法
mac 下 安装php扩展 - mcrypt
dcj3sjt126com
PHP
MCrypt是一个功能强大的加密算法扩展库,它包括有22种算法,phpMyAdmin依赖这个PHP扩展,具体如下:
下载并解压libmcrypt-2.5.8.tar.gz。
在终端执行如下命令: tar zxvf libmcrypt-2.5.8.tar.gz cd libmcrypt-2.5.8/ ./configure --disable-posix-threads --
MongoDB更新文档 [四]
eksliang
mongodbMongodb更新文档
MongoDB更新文档
转载请出自出处:http://eksliang.iteye.com/blog/2174104
MongoDB对文档的CURD,前面的博客简单介绍了,但是对文档更新篇幅比较大,所以这里单独拿出来。
语法结构如下:
db.collection.update( criteria, objNew, upsert, multi)
参数含义 参数
Linux下的解压,移除,复制,查看tomcat命令
y806839048
tomcat
重复myeclipse生成webservice有问题删除以前的,干净
1、先切换到:cd usr/local/tomcat5/logs
2、tail -f catalina.out
3、这样运行时就可以实时查看运行日志了
Ctrl+c 是退出tail命令。
有问题不明的先注掉
cp /opt/tomcat-6.0.44/webapps/g
Spring之使用事务缘由(3-XML实现)
ihuning
spring
用事务通知声明式地管理事务
事务管理是一种横切关注点。为了在 Spring 2.x 中启用声明式事务管理,可以通过 tx Schema 中定义的 <tx:advice> 元素声明事务通知,为此必须事先将这个 Schema 定义添加到 <beans> 根元素中去。声明了事务通知后,就需要将它与切入点关联起来。由于事务通知是在 <aop:
GCD使用经验与技巧浅谈
啸笑天
GC
前言
GCD(Grand Central Dispatch)可以说是Mac、iOS开发中的一大“利器”,本文就总结一些有关使用GCD的经验与技巧。
dispatch_once_t必须是全局或static变量
这一条算是“老生常谈”了,但我认为还是有必要强调一次,毕竟非全局或非static的dispatch_once_t变量在使用时会导致非常不好排查的bug,正确的如下: 1
linux(Ubuntu)下常用命令备忘录1
macroli
linux工作ubuntu
在使用下面的命令是可以通过--help来获取更多的信息1,查询当前目录文件列表:ls
ls命令默认状态下将按首字母升序列出你当前文件夹下面的所有内容,但这样直接运行所得到的信息也是比较少的,通常它可以结合以下这些参数运行以查询更多的信息:
ls / 显示/.下的所有文件和目录
ls -l 给出文件或者文件夹的详细信息
ls -a 显示所有文件,包括隐藏文
nodejs同步操作mysql
qiaolevip
学习永无止境每天进步一点点mysqlnodejs
// db-util.js
var mysql = require('mysql');
var pool = mysql.createPool({
connectionLimit : 10,
host: 'localhost',
user: 'root',
password: '',
database: 'test',
port: 3306
});
一起学Hive系列文章
superlxw1234
hiveHive入门
[一起学Hive]系列文章 目录贴,入门Hive,持续更新中。
[一起学Hive]之一—Hive概述,Hive是什么
[一起学Hive]之二—Hive函数大全-完整版
[一起学Hive]之三—Hive中的数据库(Database)和表(Table)
[一起学Hive]之四-Hive的安装配置
[一起学Hive]之五-Hive的视图和分区
[一起学Hive
Spring开发利器:Spring Tool Suite 3.7.0 发布
wiselyman
spring
Spring Tool Suite(简称STS)是基于Eclipse,专门针对Spring开发者提供大量的便捷功能的优秀开发工具。
在3.7.0版本主要做了如下的更新:
将eclipse版本更新至Eclipse Mars 4.5 GA
Spring Boot(JavaEE开发的颠覆者集大成者,推荐大家学习)的配置语言YAML编辑器的支持(包含自动提示,