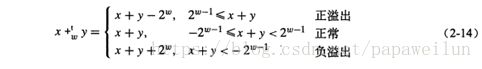csapp第二版(数据的表示~整数
----关于分析数据类型的表示范围
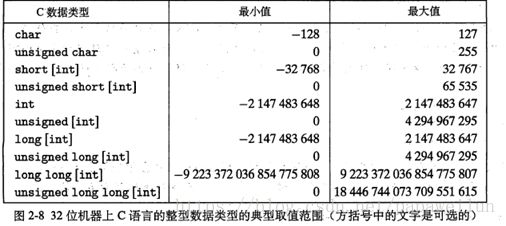
csapp 第二版 32页这个图让我们如何对一个类型进行数据分析给予了一点启示
char是被分配一个字节的,一个字节八位(8bits),没有说明是无符号的所以就认为是有符号的,根据补码规则,正数最大值为2的七次方减一等于127(因为第一位权重为2的七次方但是为了表示正数设为0)而负数的最小值为2的七次方(因为第一位权重为2的七次方,而且为了表示负数设为1)。
在这里我们可以观察到一个特点:数据类型的表示范围并不是对称的,而且很明显最大值+1=最小值的绝对值。(这个直接看或许会没有头绪,但是结合着补码的表示规则就可以很轻易的理解了。)
当然了书上除了上面一种解释,还给了一种解释,以8位表示为例,那就是当符号为1,表示复数的时候,剩下的7个位无论取1还是取0,都可以表示一个复数,那么也就是有着2的七次方等于128种可能,而当符号位为0表示正数的时候,剩下的7个位有128中可能,但是要排除一种可能,那么就是0,所以只能表示128-1=127个正数。(这样子详细的讲可能会好懂一些,原谅我的笨拙hh)
unsigned char就明显的说明了这是无符号类型的,所以说并没有符号位的概念,表示的最小数值当然就是所有位置为0,最大的当然是所有位置1,并不需要计算
2的七次方 + 2的六次方 +……2的零次方,根据二进制,只需要2的八次方-1那就是256-1=255了。
-----关于反码与补码
反码和补码一个重大的区别就是
![]()
这个会引起什么?0会出现正0和负0的出现。
在之前我的博客里面曾经说道,补码表示的那种“中间变量0”的思想,在这里就没有了,因为补码1111 1111表示的是-1,而反码表示,则是0,这一切的源头都是因为最高位的权变了。
其实这样子做无非就是为了想要把表示范围弄的对称,但是这又会出现0的两种表示方法。
我们可以发现,其实每一种数据的表示方法都有自己的利弊,并没有所谓的十全十美。
------有符号数和无符号数的转变
其实我觉得这个问题书里讲的太繁琐了,其实套用我们老师在课堂上讲的一句话
“计算机根本不知道你怎么存数据进来的,对于它们而言,只是一串比特流,只不过可以用不同的方式来解读它”
-------符号扩展
csapp 49页这里其实说明了有符号数用更大的数据类型表示的时候会使用符号扩展,而无符号数用更大的数据类型表示的时候则会使用零扩展。
说实话我觉得书本上对于符号扩展保持数据大小不变的证明有点繁琐。。。。我们可以考虑一个简单的例子
正如书上所言
我们考虑一个等式
原来的式子,设用w位来表示,现在扩展到w+1位来表示,即证明
(w位表示)-2的w-1次方+(2的w-2次方+……2的0次方)=(w+1位表示)-2的w次方+2的w-1次方+(2的w-2次方+……2的0次方)
我们可以发现,其实括号里的内容是一致的,那我们可以直接约掉
那么就是
-2的w-1次方=-2的w次方+2的w-1次方
这个是显然的。
-----整数截断
截掉不能表示的bit后还是那句话,“计算机根本不知道你怎么存数据进来的,对于它们而言,只是一串比特流,只不过可以用不同的方式来解读它”
------补码的加法溢出
不知道我理解的对不对,但是我觉得负溢出和正溢出虽然结果上感觉一样但是从细节来看还是有很大区别的。
csapp第二版58页
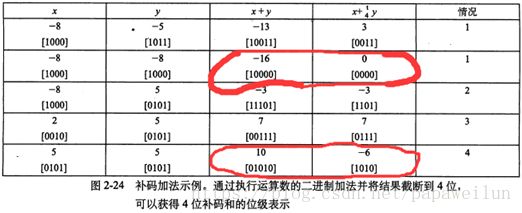
这里是4位表示示例(w=4)
我们关注这两个情况,分别是x+y之后结果小于2的w-1次方以及大于2的w-1次方-1的情况,我们会发现噢,虽然它们最终的结果都是比真值相差了2的w次方(也就是2的4次方=16),但是某种程度上是由于不同的原因造成的
第一个红色圈是负溢出,负的太多了所以反而变成正的,造成这个原因是两个有符号数相加的时候,符号位进位了,但是我们的表示范围只有4位,权值是2的w次方被自然丢弃了,所以自然地最后在机器中保留的数据会比我们期待的、真实的值加2的w次方。
第二个圈是正溢出,正的太多了所以反而变成负的,造成这个原因和权值是2的w次方位无关(因为表示正的话它都置0),起关键作用的是2的w-1次方那一位,本来在正确的表达,是正的2的w-1次方,但在自然丢弃了01010的第一个0后,1010的第一个1反而成为了负的w-1次方!这里就差了2*2的w-1次方,所以是差了2的w次方!(想一下高中在x轴讨论的距离原点的绝对值那种感觉)
虽然结果都和2的w次方有关,但某种程度上是因为不同的原因造成的。
从而得到csapp 第二版58页的结论
在学习这里的时候我会发现其实这里还会有很多讨论,例如补码的同余、模,有兴趣的大家可以查找一下关于补码的知识,我现在还在学习。。。。。。暂时无法很好的掌握,所以在这不和大家分享了)
-----补码求非
在这里我想提及的一点是,千万不要想着直接把最高位翻转一下就是求了个非啊!!!!要知道这里是补码不是原码额!
csapp第二版60页给了两种方法
第一种方法
其实我是这样子想的,两个数如果互补的话,那么相加的话就是1111(以4位表示为例,但是在补码的解读中这是-1,所以还要加一个1,所以那么就是按位求补后加1则可以得到一个关于原来用补码表示的数的非了(也就是相反数嘛))
第二种方法
我觉得这里的关键是可能观察到了如果原来的补码那个最靠近右边的bit为1的话,求反了后加1是不变的,还是1,在这里可以起到了进位传递到左边的作用。(自己的感受不一定是对的hh)
-----一些感想
其实数据表示关于位的一些探讨,其实都可以用mod运算来解决,比如【101】+【110】=【1011】(5+6=11)但实际上如果只能用3位存储,那么其实结果就是【011】(3),1=11%8=3。但其实说白了,mod8和减8不是一个意思吗。。。。。。所以说还是一种数学游戏~~