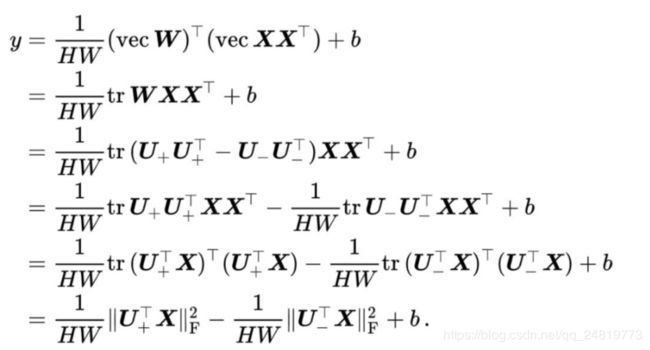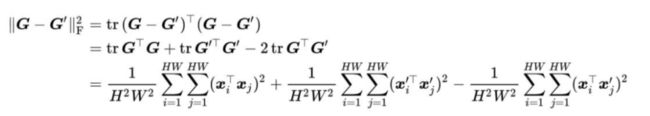双线性汇合(bilinear pooling)在细粒度图像分析及其他领域的进展综述——SIGAI推荐
目录
1. 数学准备
1.1 符号
1.2 数学性质
1.3 双线性
2. 双线性汇合
2.1 细粒度分类中的双线性汇合
2.2 不同阶的汇合
3. 精简双线性汇合
3.1 PCA降维
3.2 近似核计算
3.3 低秩双线性分类器
4. 双线性汇合的其他应用
4.1 风格迁移和纹理合成
4.2 视觉问答(visual question answering)
4.3 动作识别
5. 总结
6.参考
前言
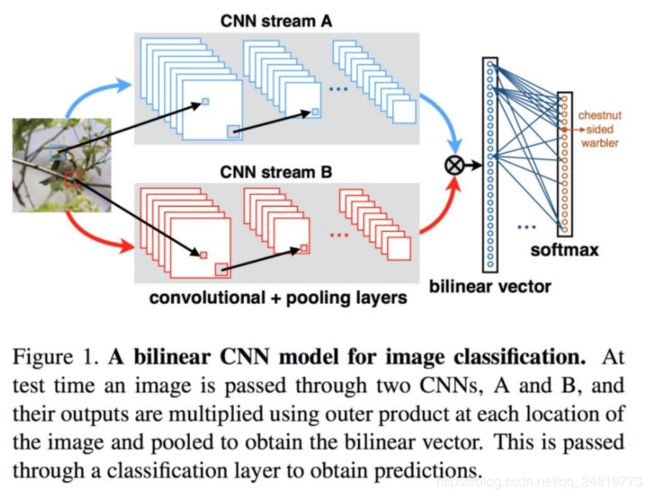
细粒度图像分类旨在同一大类图像的确切子类。由于不同子类之间的视觉差异很小,而且容易受姿势、视角、图像中目标位置等影响,这是一个很有挑战性的任务。因此,类间差异通常比类内差异更小。双线性汇合(bilinear pooling)计算不同空间位置的外积,并对不同空间位置计算平均汇合以得到双线性特征。外积捕获了特征通道之间成对的相关关系,并且这是平移不变的。双线性汇合提供了比线性模型更强的特征表示,并可以端到端地进行优化,取得了和使用部位(parts)信息相当或甚至更高的性能。
在本文,我们将对使用双线性汇合进行细粒度分类的方法发展历程予以回顾。研究方向大致分为两类:设计更好的双线性汇合过程,以及精简双线性汇合。其中,对双线性汇合过程的设计主要包括对汇合结果规范化过程的选择及其高效实现,以及融合一阶和二阶信息。精简双线性汇合设计大致有三种思路:利用PCA降维、近似核计算、以及低秩双线性分类器。此外,双线性汇合的思想也被用于其他计算机视觉领域,例如风格迁移、视觉问答、动作识别等。我们也将介绍双线性汇合在这些领域的应用。
1. 数学准备
在本节,我们介绍本文用要用到的符号和在推导时需要的数学性质。
1.1 符号
1.2 数学性质
由于双线性汇合相关的论文涉及许多矩阵运算,尤其是迹运算。如下性质在推导时将有帮助。这些性质在使用时即可以从左向右使用,也可以从右向左使用。
1.3 双线性
对函数分f(x,y),双线性(bilinear)是指当固定其中一个参数(例如x)时,f(x,y)对另一个参数(例如y)是线性的。在这里,研究的双线性函数是形如f(x,y)=XTAy这样的形式。本文关注的双线性汇合叫双线性这个名字是受历史的影响,在早期两个分支是不同的,现在主流做法是两个分支使用相同的输入,整个操作将变为非线性而不是双线性,但这个名称沿用至今。
2. 双线性汇合
双线性汇合在深度学习复兴前就已经被提出,随后,在细粒度图像分类领域得到了广泛使用。本节将介绍双线性汇合及其变体。
2.1 细粒度分类中的双线性汇合
Tsung-Yu Lin, Aruni RoyChowdhury, and Subhransu Maji. Bilinear CNN models for fine-grained visual recognition. ICCV 2015: 1449-1457.
Tsung-Yu Lin, Aruni RoyChowdhury, and Subhransu Maji. Bilinear convolutional neural networks for fine-grained visual recognition. TPAMI 2018, 40(6): 1309-1322.
在原文中,Lin等人使用了两个不同的网络得到双线性汇合的不同分支,动机是希望一个分支学到位置(where)信息,而另一个分支学到外观(what)信息。事实上,这是不可能的。
Mohammad Moghimi, Serge J. Belongie, Mohammad J. Saberian, Jian Yang, Nuno Vasconcelos, and Li-Jia Li. Boosted convolutional neural networks. BMVC 2016.
Moghimi等人提出BoostCNN,利用多个双线性CNN的boosting集成来提升性能,通过最小二乘目标函数,学习boosting权重。然而这会使得训练变慢两个量级。
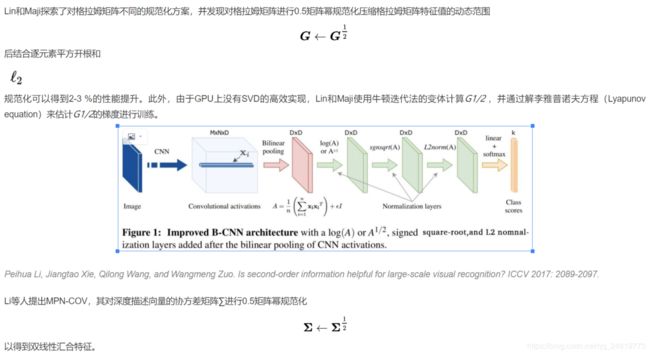
Tsung-Yu Lin and Subhransu Maji. Improved bilinear pooling with CNNs. BMVC 2017.
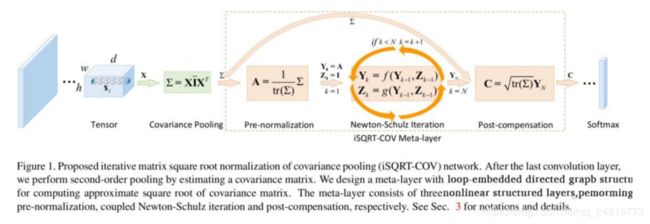
Peihua Li, Jiangtao Xie, Qilong Wang, and Zilin Gao. Towards faster training of global covariance pooling networks by iterative matrix square root normalization. CVPR 2018: 947-955.
由于在GPU上没有特征值分解和SVD的高效实现,相比Lin和Maji在反向解李雅普诺夫方程时仍需进行舒尔分解(Schur decomposition)或特征值分解,Li等人前向和反向过程都基于牛顿迭代法,来对矩阵进行0.5矩阵幂规范化。
Xing Wei, Yue Zhang, Yihong Gong, Jiawei Zhang, and Nanning Zheng. Grassmann pooling as compact homogeneous bilinear pooling for fine-grained visual classification. ECCV 2018: 365-380.
Wei等人认为,格拉姆矩阵会受视觉爆发(visual burstiness)现象的影响。视觉爆发是指一个视觉元素在同一个图片中多次出现,这会影响其他视觉元素的作用。关于视觉爆发的更多信息请参阅Herve Jegou, Matthijs Douze, and Cordelia Schmid. On the burstiness of visual elements. CVPR 2009: 1169-1176.
此外,在格拉斯曼/子空间汇合前Wei等人先对描述向量进行降维。Wei等人认为常用的使用1X1卷积核P进行降维会使得降维结果的各通道的多样性降低,因此使用P的奇异向量来降维。
Tsung-Yu Lin, Subhransu Maji, and Piotr Koniusz. Second-Order democratic aggregation. ECCV 2018: 639-656.
Lin等人使用民主聚合来使不同深度描述向量的贡献接近。
2.2 不同阶的汇合
Qilong Wang, Peihua Li, and Lei Zhang. G2DeNet: Global Gaussian distribution embedding network and its application to visual recognition. CVPR 2017: 6507-6516.
Wang等人提出G2DeNet,同时利用了一阶和二阶信息
并对其进行0.5矩阵幂规范化。
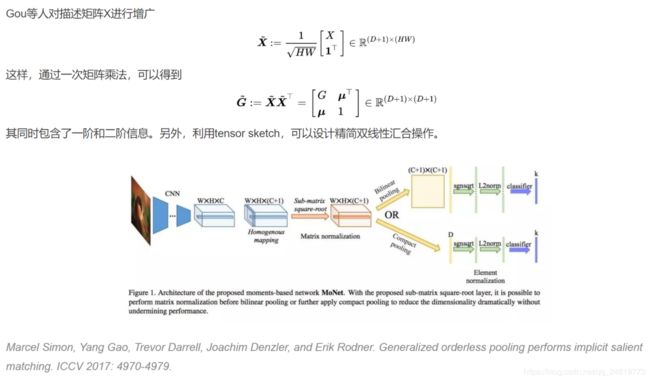
Mengran Gou, Fei Xiong, Octavia I. Camps, and Mario Sznaier. MoNet: Moments embedding network. CVPR 2018: 3175-3183.
3. 精简双线性汇合
由于格拉姆矩阵非常高维,有很多工作致力于设计精简双线性汇合,本节分别予以简要介绍。
3.1 PCA降维
Tsung-Yu Lin, Aruni RoyChowdhury, and Subhransu Maji. Bilinear CNN models for fine-grained visual recognition. ICCV 2015, pages: 1449-1457.
Tsung-Yu Lin, Aruni RoyChowdhury, and Subhransu Maji. Bilinear convolutional neural networks for fine-grained visual recognition. TPAMI 2018, 40(6): 1309-1322.
Lin等人将双线性汇合输入的一个分支先使用1*1的卷积进行降维,例如将512维降维到64维。以VGG-16为例,最终格拉姆矩阵将由R512x512降维到R512x64。在实际应用中,用PCA对这个1X1卷积的参数进行初始化。
3.2 近似核计算
Yang Gao, Oscar Beijbom, and Ning Zhang, and Trevor Darrell. Compact bilinear pooling. CVPR 2016: 317-326
实际应用中,Gao等人使用了random Maclaurin和tensor sketch两种近似,可以在达到和标准双线性汇合相似的性能,但参数量减少了90%。
关于利用FFT进行快速多项式乘法的部分,已超出本文范围。感兴趣的读者可参阅Selçuk Baktir and Berk Sunar. Achieving efficient polynomial multiplication in fermat fields using the fast Fourier transform. ACM Southeast Regional Conference 2006: 549-554.
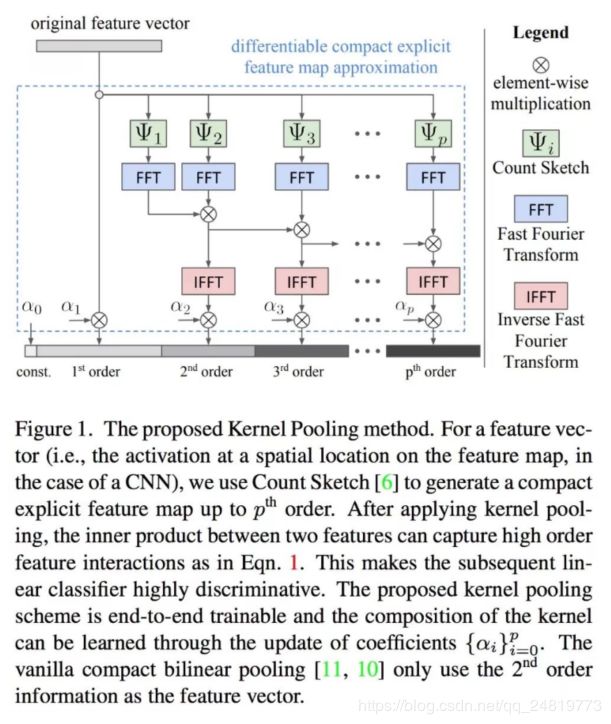
Yin Cui, Feng Zhou, Jiang Wang, Xiao Liu, Yuanqing Lin, and Serge J. Belongie. Kernel pooling for convolutional neural networks. CVPR 2017: 3049-3058.
Cui等人进一步利用核近似,借助于tensor sketch捕获更高阶的特征交互,提出核汇合。
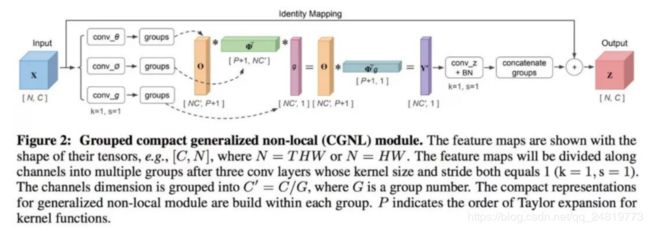
Kaiyu Yue, Ming Sun, Yuchen Yuan, Feng Zhou, Errui Ding, and Fuxin Xu. Compact generalized non-local network. NIPS 2018, accepted.
Yue等人将非局部(non-local)网络(参见下文)应用到细粒度识别中,并对核函数泰勒展开进行近似。
3.3 低秩双线性分类器
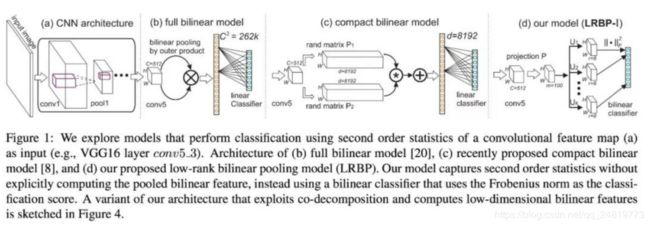
Shu Kong and Charless C. Fowlkes. Low-rank bilinear pooling for fine-grained classification. CVPR 2017: 7025-7034.
上述低秩近似还有另外一个好处。在计算图像属于各个类别的分数时
从上式可以发现,我们不再需要显式的计算双线性汇合结果。
为了进一步降低参数矩阵的计算量,LRBP对参数矩阵做了第二次近似。由于细粒度识别问题中各类有公共结构,因此,LRBP将对应各类别的参数矩阵近似为Wk=PVk,其中P∈RD*m,m是另一个超参数。不同类别的参数矩阵 P是共享的,实际中,P和Vk都由1X1卷积实现。P由PCA投影矩阵初始化,而Vk采用随机初始化。
Yanghao Li, Naiyan Wang, Jiaying Liu, and Xiaodi Hou. Factorized bilinear models for image recognition. ICCV 2017: 2098-2106.
Li等人通过对参数矩阵进行低秩近似来完成图像分类任务,同时其也包含了一阶信息。Li等人所提出的的FBN结构可以用于所有的卷积和全连接层。
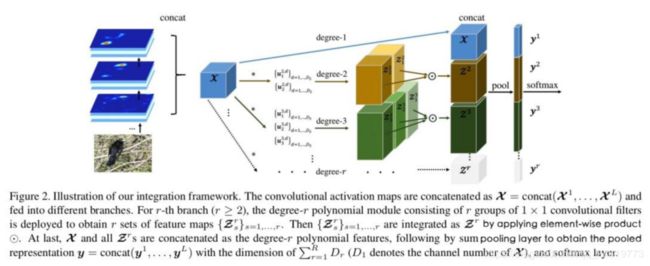
Sijia Cai, Wangmeng Zuo, and Lei Zhang. Higher-order integration of hierarchical convolutional activations for fine-grained visual categorization. ICCV 2017: 511-520.
Cai等人捕获了更高阶的特征交互,并对参数进行秩1近似。
Kaicheng Yu and Mathieu Salzmann. Statistically-motivated second-order pooling. ECCV 2018: 621-637.
Yu和Salzmann对参数矩阵进行低秩近似,并给双线性汇合的每一步一个概率上的解释。这个操作可以被等价为对深度描述向量进行1X1卷积后在 l2 汇合。
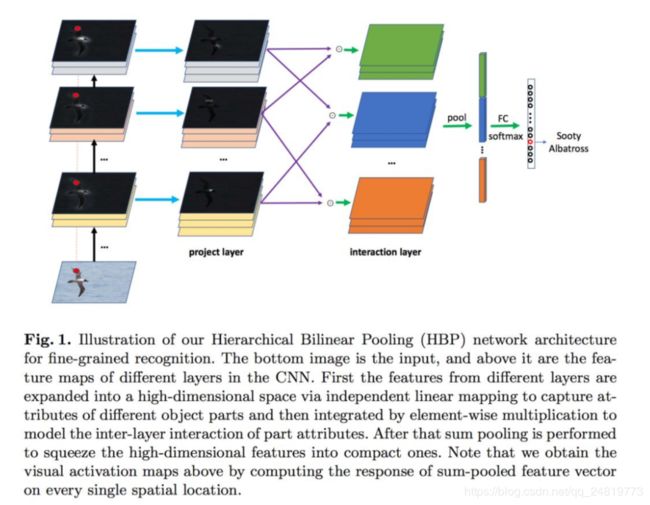
Chaojian Yu, Xinyi Zhao, Qi Zheng, Peng Zhang, and Xinge You. Hierarchical bilinear pooling for fine-grained visual recognition. ECCV 2018: 595-610.
类似于MLB(见下文),对参数矩阵进行低秩近似
并使用不同层的深度描述向量作为x和z。
4. 双线性汇合的其他应用
4.1 风格迁移和纹理合成
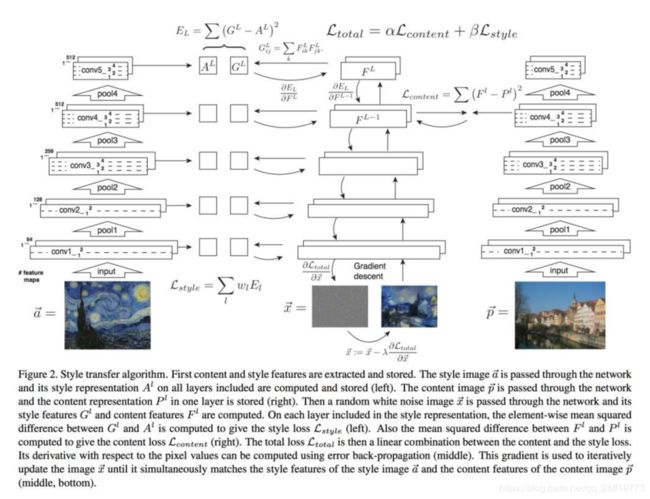
Leon A. Gatys, Alexander S. Ecker, Matthias Bethge. Image style transfer using convolutional neural networks. CVPR 2016: 2414-2423.
风格迁移的基本思路是使优化目标包括两项,使生成图像的内容接近原始图像内容,及使生成图像风格接近给定风格。风格通过格拉姆矩阵体现,而内容则直接通过神经元激活值体现。
Yanghao Li, Naiyan Wang, Jiaying Liu, and Xiaodi Hou. Demystifying neural style transfer. IJCAI 2017: 2230-2236.
Li等人发现,考虑一张训练图像和一张测试图像对应的格拉姆矩阵G和G',风格损失项
这里利用了上文Compact bilinear pooling的推导结果。这对应了深度描述向量之间的二阶多项式MMD距离。最小化风格损失就是在最小化这两者的特征分布。
4.2 视觉问答(visual question answering)
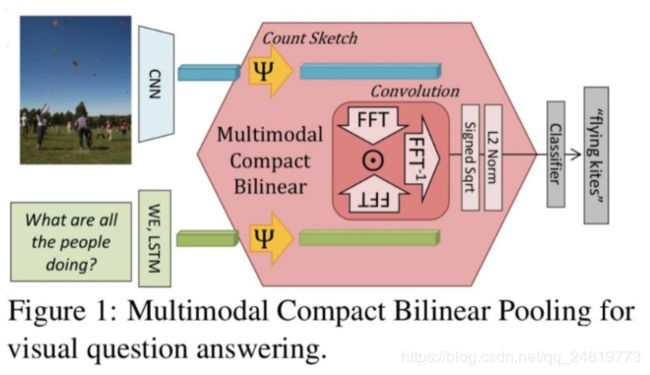
Akira Fukui, Dong Huk Park, Daylen Yang, Anna Rohrbach, Trevor Darrell, and Marcus Rohrbach. Multimodal compact bilinear pooling for visual question answering and visual grounding. EMNLP 2016: 457-468.
Fukui等人提出MCB,对图像和文本特征进行精简双线性汇合。
Jin-Hwa Kim, Kyoung Woon On, Woosang Lim, Jeonghee Kim, JungWoo Ha, and Byoung-Tak Zhang. Hadamard product for low-rank bilinear pooling. ICLR 2017.
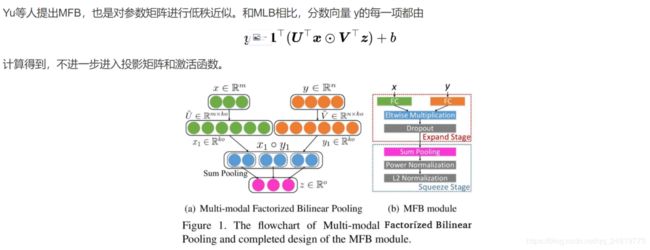
Zhou Yu, Jun Yu, Jianping Fan, and Dacheng Tao. Multi-modal factorized bilinear pooling with co-attention learning for visual question answering. ICCV 2017: 1839-1848.
Zhou Yu, Jun Yu, Chenchao Xiang, Jianping Fan, and Dacheng Tao. Beyond bilinear: Generalized multi-modal factorized high-order pooling for visual question answering. TNNLS 2018, in press.
4.3 动作识别
Rohit Girdhar and Deva Ramanan. Attentional pooling for action recognition. NIPS 2017: 33-44.
5. 总结
本文介绍了双线性汇合在细粒度图像分类及其他计算机视觉领域的应用。研究方向大致分为两类,设计更好的双线性汇合过程,以及精简双线性汇合。未来可能的研究方向包括以下几个部分
- 双线性汇合结果的规范化。目前发现矩阵幂规范化对提升性能很有帮助,是否还有其他规范化方法,以及能否设计出其在GPU的高效实现?
- 精简双线性汇合。目前研究的一大关注点是对参数矩阵进行低秩近似,是否还有其他精简双线性汇合方法?
- 双线性汇合原理。目前对双线性汇合原理的理解围绕着深度描述向量之间的二阶多项式核展开,是否还有其他对双线性汇合原理的理解方法?
此外,经典双线性汇合官方源代码是基于MatConvNet实现,这里提供一个基于PyTorch的实现版本:
https://github.com/HaoMood/bilinear-cnn
6.参考
SIGAI公众号