线性分类-感知机，线性判别分析，逻辑回归，高斯判别分析，朴素贝叶斯

线性分类

从线性回归到线性分类，通过激活函数或者降维来实现。

线性回归函数$f(w,b)=w^{T}x+b$经过激活函数作用$y=f(w^{T}x+b)$作用后变成硬分类问题$yϵ\left\{0,1\right\}$或者变成软分类问题$yϵ[0,1],$函数$f$就称为激活函数，$f^{-1}$称为$linkfunction,$
硬分类代表模型：感知机，线性判别分析
软分类代表模型：高斯判别分析(生成式模型)，逻辑回归(判别式模型)

硬输出-感知机

样本集：${\left\{(x_i,y_i)\right\}}_{i=1}^N$
感知机思想：错误驱动。给定一个初始的分类平面$w^{T}x，$再一步步移动这个平面使得被错误分类的点越来越少。被错误分类的集合用D表示
模型：$f(x)=sign(w^{T}x),xϵR^P,wϵR^P,$其中当
$$w^{T}x\ge 0,sign(w^{T}x)=1;w^{T}x<0,sign(w^{T}x)=0$$
策略定义为被错误分类的点的个数
策略：$lossfunction:L(w)={\sum }_{i=1}^{N}I\left\{y_i{w}^T{x}_i<0\right\},$也就是当$y_i{w}^T{x}_i<0$时样本是被错误分类的。
通俗点理解就是$w^T{x}_i>0,y_i=1\to y_i{w}^T{x}_i>0,$分类正确，反之分类错误。然而$L(w)$是不可导的，那么这个$lossfunction$就需要进行改进。虽然$L(w)$是不可导的，但是$y_i{w}^T{x}_i$是可导的。
因此改进之后的$lossfuntion$是这样：$L(w)={\sum }_{x_iϵD}-y_i{w}^T{x}_i，$
对$w$求偏导：${▽}_{w}L=-y_i{x}_i$
接下来算法只需用随机梯度下降法就能求出来了。
算法:SGD
$$w^{(t+1)}\leftarrow w^t+\lambda {▽}_{w}L$$

当然，上述的感知机算法都是基于数据线性可分为前提

硬输出-线性判别分析

样本集：${\left\{(x_i,y_i)\right\}}_{i=1}^N,x_iϵR^p,y_iϵ\left\{c_1=1,c_2=-1\right\}$
$x_{c_1}=\left\{x_i|y_i=+1\right\},x_{c_2}=\left\{x_i|y_i=-1\right\}$
令集合$x_{c_1}=N_1,x_{c_2}=N_2,$所以$N_1+N_2=N$
思想：类内小，类间大
如图所示：

同类的数据间隔尽量小(类内方差尽量小)，而不同类数据星星和圈圈之间的距离尽量大(类间大)。
我们投影的方向是$w,$也就是超平面对应的法向量。
点到平面的投影的线为$z，z_i=w^T{x}_i$

所以不同类的均值可以表示出来：

那么类间的距离就可以用$({\bar{z}}_1-{\bar{z}}_2{)}^2$表示；
类内的距离就用$S_1+S_2$表示。
那么为了达到我们的目的，也就是类内小，类间大，目标函数可以定义如下：

令：

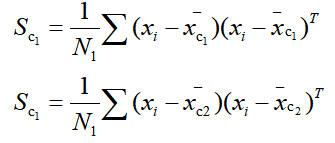
化简我们的$J(w)$表达式，可得：


这里的$S_b$就是类间方差，$S_w$是类内方差。
对w求偏导，令$\frac{\partial J(w)}{\partial w}=0，$求得：

由于我们只关心$w$的方向而不管其大小，那么$w\propto S_w^{-1}({\bar{x}}_{c_1}-{\bar{x}}_{c_2})$；如果$S_w^{-1}$是个对角矩阵或者单位矩阵，那么$w\propto ({\bar{x}}_{c_1}-{\bar{x}}_{c_2})$

软输出-判别式：逻辑回归

样本集：${\left\{(x_i,y_i)\right\}}_{i=1}^N,x_iϵR^p,y_iϵ\left\{0,1\right\}$

引入sigmoid function：

其函数图像如下：

代入有：

接下来用极大似然估计求解$\hat{w}=\underset{w}{\mathrm{argmax}}logP(Y|X)$就可以了。

软输出-生成式：高斯判别分析

样本集：${\left\{(x_i,y_i)\right\}}_{i=1}^N,x_iϵR^p,y_iϵ\left\{0,1\right\}$

我们知道对于概率判别模型，我们可以直接求y值进行分类；而概率生成模型则是通过比较y=0和y=1的大小进行判断，根据贝叶斯公式$P(y|x)=\frac{P(x|y)P(y)}{P(x)}$我们知道，概率生成模型和分母项$P(x)$无关，所以可以对联合概率建模$P(y|x)\propto P(x|y)P(y)，$也就是后验=似然*先验。

模型：$\hat{y}=\underset{yϵ\left\{0,1\right\}}{\mathrm{argmax}}P(y|x)=\underset{y}{\mathrm{argmax}}P(y)P(x|y)$

那么y是服从伯努利分布$P(y)={\varphi }^y(1-\varphi {)}^{1-y}$，

x服从于高斯分布,$x|y=1\sim N({\mu }_1,\epsilon {)}^y$,$\left\{x_i|y_i=1,i=1,...,N\right\}$,此集合作为$c_1$,集合内元素的总个数为$N_1$，对应的方差为$S_1$。
$x|y=0\sim N({\mu }_2,\epsilon {)}^y$,$\left\{x_i|y_i=0,i=1,...,N\right\}$,集合作为$c_2$,集合内元素的总个数为$N_2$，对应的方差为$S_2$。

$P(x_i|y_i)=N({\mu }_1,\epsilon {)}^y\ast N({\mu }_2,\epsilon {)}^{1-y}$

对数似然就能写成如下公式：

求得$\hat{\varphi }=\frac{N_1}{N},$

$\hat{\epsilon }=\frac{1}{N}(N_1{S}_{!}+N_2{S}_2)$

${\hat{\mu }}_1=\frac{\sum i=1N{y}_i{x}_i}{N_1}$

${\hat{\mu }}_2=\frac{\sum i=1N{y}_i{x}_i}{N_2}$

软输出-生成式：朴素贝叶斯

样本集：${\left\{(x_i,y_i)\right\}}_{i=1}^N,x_iϵR^p,y_iϵ\left\{0,1\right\}$

思想：朴素贝叶斯假设，也叫条件独立性假设。
朴素贝叶斯是最简单的概率图(有向图)模型。
条件独立性假设如图所示:

也就是给定y的情况下，x1和x2相互独立。

做这个假设的目的就是为了简化运算，考虑高维情况。

朴素贝叶斯的目的也是给定x和y，判断其属于0还是1。
模型：

对于P(y)，如果是二分类问题，其属于伯努利分布；如果是多分类问题，其属于categrial分布。
对于P(x|y),假定其遵循条件独立性假设。如果x是离散的，其属于categorical分布；如果x是连续的，其属于高斯分布。

求解可以直接用极大似然估计求解出来，在此就不做过多介绍了。