降维--PCA,特征选择
降维
- 引入原因
- 均值和方差的矩阵形式
- PCA
- 最大投影方差
- 最小重构代价
- PCA算法描述
引入原因
为了防止过拟合,我们通常的解决办法有:增加数据,正则化,降维等方法。
为什么要引入降维呢?
当数据量过大特征过多的时候,数据的维度过高有可能会导致维度灾难。在没有更过数据进行补充的情况下,一般都是做降维处理。
而且在高维情况下,数据会越来越稀疏,并且数据会分布在样本空间的边缘地区,这绝对不是我们想要的结果。
下面看看降维的主要方法:
降维的主要方法:
1.直接降维----特征选择
2.线性降维----PCA,MDS
3.非线性降维----isomap,LLE
均值和方差的矩阵形式
引入数据: X = ( x 1 , x 2 , . . . , x N ) N × P T = ( x 1 T . . . x N T ) = ( x 11 . . . x 1 p . . . x N 1 . . . x N p ) N × P X=(x_1,x_2,...,x_N)_{N×P}^T=\begin{pmatrix} x_1^T\\ ...\\ x_N^T \end{pmatrix}=\begin{pmatrix} x_{11} & ... &x_{1p}\\ .& .& .\\ x_{N1}& ... &x_{Np} \end{pmatrix}_{N×P} X=(x1,x2,...,xN)N×PT=⎝⎛x1T...xNT⎠⎞=⎝⎛x11.xN1.......x1p.xNp⎠⎞N×P
样本均值: x ˉ p × 1 = 1 N ∑ x i \bar x_{p×1}=\frac{1}{N}\sum x_i xˉp×1=N1∑xi
样本方差: S p × p = 1 N ∑ i = 1 N ( x i − x ˉ ) ( x i − x ˉ ) T S_{p×p}=\frac{1}{N}\sum_{i=1}^{N}(x_i-\bar x)(x_i-\bar x)^T Sp×p=N1∑i=1N(xi−xˉ)(xi−xˉ)T
将上面的均值和方差写成矩阵形式:
样本均值: x ˉ = 1 N ∑ x i = 1 N ( x 1 , . . . , x ˉ ) ( 1 . . . 1 ) = 1 N X T 1 N \bar x=\frac{1}{N}\sum x_i=\frac {1}{N}(x_1,...,\bar x)\begin{pmatrix} 1\\ ...\\ 1 \end{pmatrix}=\frac{1}{N}X^T1_N xˉ=N1∑xi=N1(x1,...,xˉ)⎝⎛1...1⎠⎞=N1XT1N
样本方差:
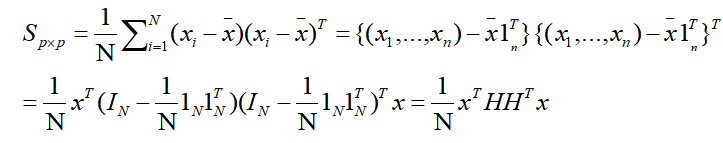
上式中的H矩阵,我们称为中心矩阵。H具有一些特殊的性质,如: H T = H , H N = H H^T=H,H^N=H HT=H,HN=H
PCA
主成分分析是最常用的一种降维方法。
给定一个特征空间,如何用一个超平面对所有的样本进行恰当的划分?
我们可以想象到的,如果存在这样一个超平面,那么它应该具有这样两种性质:
1.最大投影方差。
2.最小重构距离。
也即是样本点到这个超平面的距离都足够近,样本点在这个超平面上的投影尽量能分开。
那我们就从这两个角度分别看看PCA的推导
最大投影方差
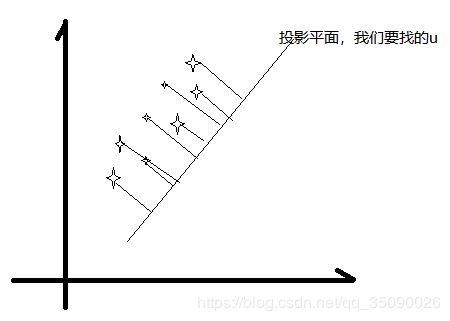
假设我们要找的方向是 u , u, u,
第一步,中心化。中心化的目的是为了方便计算。做法就是用样本-均值 x i − x ˉ , x_i-\bar x, xi−xˉ,将样本都集中在坐标轴附近。
假定我们要找的方向就是 u 1 , u_1, u1,并且它的模 ∣ ∣ u 1 ∣ ∣ = 1. ||u_1||=1. ∣∣u1∣∣=1.我们的数据 x i − x ˉ x_i-\bar x xi−xˉ到找的向量 u 1 u_1 u1的距离就是 ( x i − x ˉ ) T u 1 (x_i-\bar x)^Tu_1 (xi−xˉ)Tu1。
投影我们用 J J J表示,N个点的投影方差就是:
J = 1 N ∑ i = 1 N [ ( x 1 − x ˉ ) T u 1 ] 2 J=\frac{1}{N}\sum_{i=1}^{N}[(x_1-\bar x)^Tu_1]^2 J=N1∑i=1N[(x1−xˉ)Tu1]2
= ∑ i = 1 N 1 N u 1 T ( x 1 − x ˉ ) ( x 1 − x ˉ ) T u 1 =\sum_{i=1}^{N}\frac{1}{N}u_1^T(x_1-\bar x)(x_1-\bar x)^Tu_1 =∑i=1NN1u1T(x1−xˉ)(x1−xˉ)Tu1
= u 1 T [ ∑ i = 1 N 1 N ( x 1 − x ˉ ) ( x 1 − x ˉ ) T ] u 1 =u_1^T[\sum_{i=1}^N\frac{1}{N}(x_1-\bar x)(x_1-\bar x)^T]u_1 =u1T[∑i=1NN1(x1−xˉ)(x1−xˉ)T]u1
= u 1 T S u 1 =u_1^TSu_1 =u1TSu1
最后我们要找的 u 1 u_1 u1就出来了,
u ^ 1 = a r g m a x u 1 T S u 1 \hat u_1=argmaxu_1^TSu_1 u^1=argmaxu1TSu1
s . t . u 1 T u 1 = 1 s.t.u_1^Tu_1=1 s.t.u1Tu1=1
用拉格朗日乘子法对其求解,可以得到 S u 1 = λ 1 u 1 Su_1=\lambda_1 u_1 Su1=λ1u1最终的结果。之后对协方差矩阵 S S S进行特征值分解求得特征值,这就是主成分分析的解。
最小重构代价
换个角度,我们转换一下坐标系也就是把 u 1 , u 2 u_1,u_2 u1,u2作为坐标轴,原先的点可以表示维 x i = ( x i T u 1 ) u 1 + ( x i T u 2 ) u 2 x_i=(x_i^Tu_1)u_1+(x_i^Tu_2)u_2 xi=(xiTu1)u1+(xiTu2)u2

PCA算法描述
输入:样本集 D = { x 1 , x 2 , . . . , x m } D=\left \{ x_1,x_2,...,x_m\right \} D={x1,x2,...,xm},低维空间维数 d ′ d' d′。
过程:
1.对书友样本进行中心化: x i < − − x i − 1 m ∑ i = 1 m x i x_i<--x_i-\frac{1}{m}\sum_{i=1}^{m}x_i xi<−−xi−m1∑i=1mxi;
2.计算样本的协方差矩阵 X X T XX^T XXT
3.对协方差矩阵 X X T XX^T XXT做特征值分解
4.取最大的 d ′ d' d′个特征值对应的特征向量 w 1 , w 2 , . . . , w d w_1,w_2,...,w_d w1,w2,...,wd。
输出:投影矩阵 W ∗ = ( w 1 , w 2 , . . . , w d ′ ) W^*=(w_1,w_2,...,w_{d'}) W∗=(w1,w2,...,wd′)
上面算法中的维数 d ′ d' d′通常由用户事先指定。而且低维空间和高维空间有所不同,因此对应最小的 d − d ′ d-d' d−d′个特征值的特征向量被舍弃了,这就是降维导致的结果。但是舍弃这部分信息并不代表不好:数据受到噪声影响的时候,最小的特征值对应的特征向量往往和噪声有关,舍弃他们在一定程度上有降噪的效果;另一方面,舍弃后我们的采样密度也会更大,而这也正是我们的动机。