C++-数据结构-堆排序

目录

 

堆排序

1、 最大堆定义：

2、如何将随机数组生成一个最大堆？

3、堆排序

---

堆排序

1、 最大堆定义：

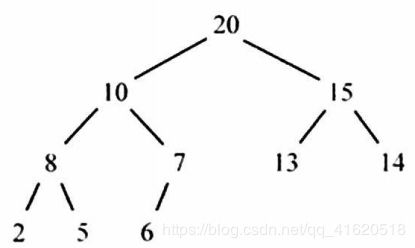
例如下面的这个例子：就是一个最大堆

2、如何将随机数组生成一个最大堆？

1）源代码：

#include 
using namespace std;

template
void heapify(T data[], int first, int size)//first为最先执行堆化的数组索引
{
	int largest = 2 * first + 1;//永远取得是靠左边的数，因为largest永远是基数
	while (largest <= size-1) {
		//比较堆中左右二值，取较大值的索引；
		//注意此时要有largest < size - 1的判定条件，不然data[largest + 1]将会超出索引范围。
		//当largest = size - 1时，说明最末尾的节点不需要比较，因为不存在左右节点。
		if (largest < size - 1 && data[largest] < data[largest + 1]) { largest++; }
		//父节点与子节点中的较大值比较
		if (data[first] < data[largest]) {
			swap(data[first], data[largest]);
			//由于交换了父子节点，可能对其所在的堆产生影响，例图(c)
			//因此需要在进行一次堆化，针对子节点
			first = largest;
			largest = 2 * first + 1;//倘若largest>size-1，说明此子节点无子节点。
		}
		else
			largest = size;//用于退出循环
			               //由于堆化的顺序是从下至上的，因此上堆不需要堆化则下堆一定不用堆化。
	}
}


template
void printdata(T data[], int n)
{
	for (int i = 0;i < n;++i)//注意，这里不能用i<=n
		cout << data[i] << "    ";
}

int main() {
	int data[] = { 2,8,6,1,10,15,3,12,11 };
	for (int i = 9 / 2 - 1;i >= 0;--i)//9是数组长度，堆化执行顺序是从最末尾开始。
		heapify(data, i, 9);
	printdata(data, 9);
	system("pause");
	return 0;
}

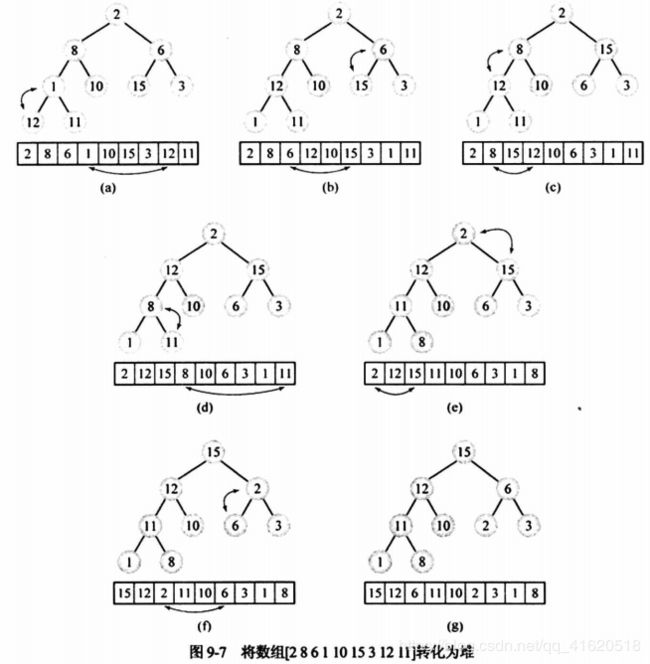
2）图解

 先从main函数开始讲解：

1）floor(数组长度/2)指的是堆中有多少个小堆，例如图(a)中就有4个小堆（父节点与子节点的结合），分别是2,8,6；8,1,10；6,15,3；1,12,11。

2）当进入heapify函数时，data[largest]是指向子节点中靠左边的数，例如图(a)中的8,1,15,12。同时，data[first]指向data[largest]的父节点。

3）此后详细见代码注释。

4）注意此函数仅仅为生成一个最大堆，而并非进行堆排序。

3、堆排序

1）基本思想：

先根据数组建立最大堆，然后依次将堆顶元素（最大值）放置在堆的末尾，交换后新的堆顶R[1]可能违反堆的性质，因此重新堆化（忽略已经排序好的数组），再次得到堆顶元素（最大值），放置在堆的末尾，重复n-1次。

2）算法描述（建议先用简单数组演示代码后在看算法描述以及动图演示）

      a）将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；

      b）将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；

      c）由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

3)源代码：

int main() {
	int data[] = { 2,8,6,1,10,15,3,12,11 };
	//初始数组堆化
	for (int i = 9 / 2 - 1;i >= 0;--i)//9是数组长度，堆化执行顺序是从最末尾开始,从下到上，从左到右。
		heapify(data, i, 9);
	//堆化后则数组最大值位于data[0]
	for (int i = 9 - 1;i >= 1;--i) {
		//将data[0]与data中的最后一位交换，将最大值放在末尾处
		swap(data[0], data[i]);
		//此次堆化是从上至下，因为此数组已经堆化好
		//只需对调换了位置的数值所在的堆进行堆化即可
		//通过i的自减来控制输入参数size的数值，做到忽略已排序好的末尾数组。
		heapify(data, 0, i);
	}
	printdata(data, 9);
	system("pause");
	return 0;
}