单源最短路径（Dijkstra算法）

迪杰斯特拉（Dijkstra）算法

定义

Dijkstra(迪杰斯特拉)算法是计算单源最短路径算法，用于计算一个结点到其他所有结点的最短路径。该算法以源点为起始点，不断更新其他点到已经确定距离结点的距离，选取距离最小的结点加入S集合，直到S集合存放有所有的结点

算法思想

现在一张图中有n个结点，有两个集合，S集合和V集合。S集合表示已经选取的结点，V集合表示还没有选取的结点

1. 确定一个源点，放入S集合，剩下n-1个结点放入V集合
2. 计算从源点经过S集合中的各点到达V集合中各点的距离，与之前确定的距离进行比较，如果新计算的距离小于原先的距离则更新该结点的距离，否则不更新距离，并选取距离最小的结点放入S集合，直到V集合为空（在计算过程中直接计算从最后加入S集合的点到源点的距离+最后加入S集合的点到V集合中各点的距离，表示从源点到达V集合中各点要经过最后加入S集合中的点，与原来的距离比较即可）

还是很抽象，举个例子

示例

我们以有向图为例

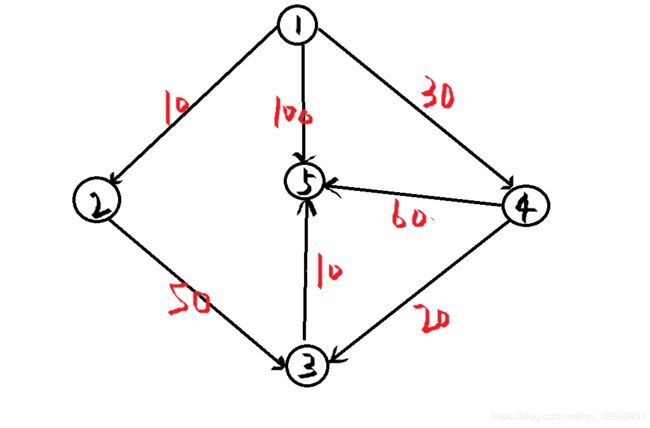
比如我们选取结点1为源点，利用Dijkstra算法计算源点到其他各点的距离
那么现在S=[1]，V=[2，3，4，5]
计算此时从源点出发经过最后加入S集合中的点（源点）到达V集合中各点的距离
经过S集合中的各点到达2的距离：10
经过S集合中的各点到达3的距离：inf
经过S集合中的各点到达4的距离：30
经过S集合中的各点到达5的距离：100
此时选取距离最小的结点2加入S集合，即S=[1,2]，V=[3,4,5]

计算此时从源点出发经过最后加入S集合中的点（结点2）到达V集合中各点的距离
如果新计算的距离小于原先得距离则更新该结点的距离，否则不更新距离
源点到结点2的距离+结点2到V集合中结点3的距离：10+50=60，小于inf，更新
源点到结点2的距离+结点2到V集合中结点4的距离：10+inf，不小于原来的30，不更新
源点到结点2的距离+结点2到V集合中结点5的距离：10+inf，不小于原来的100，不更新
故：
3：60
4：30
5：100
此时选取距离最小的结点4加入S集合，即S=[1,2,4]，V=[3,5]

计算此时从源点出发经过最后加入S集合中的点（结点4）到达V集合中各点的距离，如果新计算的距离小于原先得距离则更新该结点的距离，否则不更新距离
源点到结点4的距离+结点4到V集合中结点3的距离：30+20=50，小于原来的60，更新
源点到结点4的距离+结点4到V集合中结点5的距离：30+60=90，小于原来的100，更新
故：
3：50
5：90
此时选取距离最小的结点3加入S集合，即S=[1,2,4,3]，V=[5]

计算此时从源点出发经过最后加入S集合中的点（结点3）到达V集合中各点的距离
源点到结点3的距离+结点3到V集合中结点5的距离：50+10=60，小于原来的90，更新
故：
5：60
此时选取距离最小的结点5加入S集合，即S=[1,2,4,3,5]，V=[ ]

因为在生成最短路径的过程中，从源点到达V集合中各点时都要经过S集合中的各点，故生成的最短路径如下：

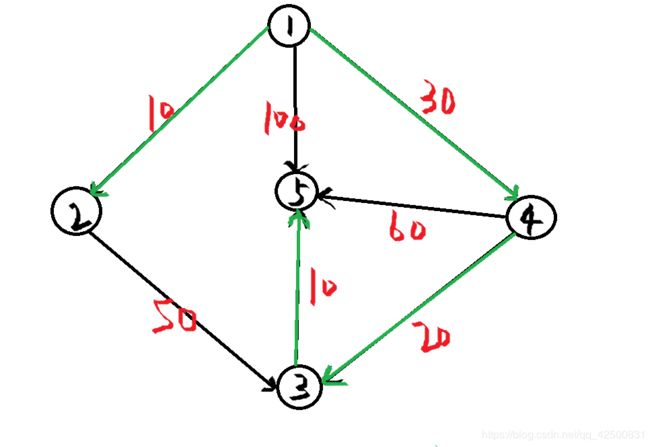
在加入顶点的过程中我们得到了单源最短路径，从源点到2，3，4，5的距离分别为：10，50，30，60

代码

#include

using namespace std;

const int inf = INT_MAX; 

void Dijkstra(int n,int source,int *dist,int *prev,int c[5][5])
{
	//接下来先进行初始化操作
	bool s[n];//用于表示点是否在s集合里 
	for(int i=0; i<n; i++){
		dist[i] = c[source][i];
		if(i != source)  s[i] = false;//初始化的时候，除了source外所有的点都不在 s集合 
		else s[i] = true;
        if(dist[i] == inf) prev[i] = -1;//结点暂时不可达，前驱结点记作-1
		else prev[i] = source;//此时结点可达，表示与源结点相邻，前驱点是源点 
	} 

	for(int i=1; i<n; i++)//没有用到i的值，只是控制循环次数,表示要找n-1个点 
	{
		int minDist = inf;
		int newNode;//u记录下距离source最近的点
		
		for(int j=0; j<n; j++){	//从v-s集合中找点 
			//j点不在s集合中，且到source的距离小于上一个点到source的距离，就用u记录下该点 
			if(!s[j] && dist[j]<minDist){
				newNode = j;
				minDist = dist[newNode];
			}
		}
		
		s[newNode] = true;//将u点加入s集合
		
		for(int j=0; j<n; j++){//当s集合加入新点的时候需要更新dist[]和prev[] 
			if(!s[j] && c[newNode][j]<inf){//j点不在s集合中，且 新点与 j点相邻 
				int newDist = dist[newNode] + c[newNode][j];//新点到source的距离 + 新点到 j点的距离
				if( newDist < dist[j] ){
				    dist[j] = newDist;
					prev[j] = newNode;//新点成了j的前驱点，表示此时从source到j点经过u距离最短 
				}
			}
		} 
	} 
}

int main()
{
	/*
	n个点
	dist[i]表示从source点到 i点的最短距离
	k=previous[i]表示经过 k点到达 i点才是最短路径 
	c[][]是临接矩阵 
	*/ 
	
	int c[5][5]={
					{0,10,inf,30,100},
					{inf,0,50,inf,inf},
					{inf,inf,0,inf,10},
					{inf,inf,20,0,60},
					{inf,inf,inf,inf,0}
				};
	int n = 5;
	int dist[n];
	int prev[n];
	int source = 0;
	
	Dijkstra(n,source,dist,prev,c);	
	cout<<"源点到各点的最短距离为：";
	for(int i=0; i<n; i++){
		cout<<dist[i]<<" ";
	}
	return 0;
}

运行结果