LeetCode刷题(1-30)
LeetCode刷起来,时间成本好高,呜呜。。。
文章目录
- 1、两数之和(哈希表)
- 2、两数相加(链表)
- 3、无重复字符的最长字串(滑动窗口)
- 4、寻找两个正序数组的中位数(二分法,重要!)
- 5、最长回文子串(dp)
- 6、Z字型变换(了解)
- 7、整数反转(取模、求商)
- 8、字符串转成整数
- 9、回文数(取模、求商)
- 10、正则表达式匹配(dp)
- 11、盛最多水的容器(双指针)
- 13、罗马数字转整数(哈希表)
- 14、最长公共前缀(字符串)
- 15、三数之和(数组--双指针)
- 16、最接近的三数之和(数组--双指针)
- 18、四数之和(数组--双指针)
- 19、 删除链表的倒数第N个节点(快慢指针)
- 20、有效的括号(栈)
- 21、合并两个有序链表(链表)
- 22、括号生成(递归回溯)
- 23、合并K个排序链表(链表)
- 26、删除排序数组中的重复项(双指针)
- 27、移除元素(双指针)
- 28、实现 strStr() 函数
- 29、两数相除
- 30、串联所有单词的子串(滑动窗口)
1、两数之和(哈希表)
题目:给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
1、思路:
存储数据一般能想到的就是数组、链表、哈希表:
数组是易于查找不易于增删,链表是易于增删不易于查找,而且在数据量很大的时候,他们的劣势会十分明显。对于大数据的数据存储,适合用hash表。hash表是数组和链表的结合体,在一定的情况下,它能拥有数组和链表的优点。
想要查询数组中的某一个数时,需要遍历整个数组才能查到。想要查询练哈希表的某一个数时,直接通过hash算法计算出桶下标就可以查询出值,时间复杂度O(1)
1、由于哈希查找的时间复杂度为 O(1),所以可以利用哈希容器 map 降低时间复杂度
2、使用map的key存放数组中的值,使用value存放数组的索引
3、遍历数组,判断map中是否存在target-nums[i]的key值,如果存在返回下标索引,如果不存在就添加到map中

4、时间复杂度:遍历数组的长度为O(n)
2、代码:
/**
* 给定 nums = [2, 7, 11, 15], target = 9
*
* 因为 nums[0] + nums[1] = 2 + 7 = 9,所以返回 [0, 1]
*
* time:O(n)
* space:O(n)
*/
public class Solution {
public int[] twoSum(int[] nums, int target) {
HashMap<Integer,Integer> map = new HashMap<>();
for(int i=0;i<nums.length;i++){
if(map.containsKey(target-nums[i])){
return new int[]{map.get(target-nums[i]),i};
}
map.put(nums[i],i);
}
return null;
}
}
/**
time:O(n) :遍历一遍数组
space:O(n)
*/
2、两数相加(链表)
题目:给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
1、思路
1、将两个链表看成是相同长度的进行遍历,如果一个链表较短则在后面补 0
2、链表逆序存储数字的位数,链表对应位相加,如果进位表现为往后进1(正常为往前)
3、如果两个链表全部遍历完毕后,进位值为1,则在新链表后面加节点1
小技巧:对于链表问题,返回结果为头结点时,通常需要先初始化一个预先指针 pre,该指针的下一个节点指向真正的头结点head。使用预先指针的目的在于链表初始化时无可用节点值,而且链表构造过程需要指针移动,进而会导致头指针丢失,无返回结果。
2、代码
/**
* 输入:(2 -> 4 -> 3)
* + (5 -> 6 -> 4)
* 输出:7 -> 0 -> 8
*
* 原因:342 + 465 = 807
*/
class ListNode {
int val;
ListNode next;
//节点类的构造函数
ListNode(int x) {
val = x;
}
}
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
/**
* 1、如果需要返回头结点,通常预先定义一个dummy节点,该节点的next指针指向真正的头结点
* 2、定义两个指针 cur1、cur2 分别用来遍历两个链表
* 3、初始化一个变量 sum,用来存放链表节点相加的和
* 4、因为 dummy节点不能动,因此定义一个cur指向dummy,用来遍历新链表
*/
ListNode dummy = new ListNode(0);
ListNode cur1 = l1;
ListNode cur2 = l2;
int sum = 0;
ListNode cur = dummy;
/**
* 1、遍历两个链表
* 2、将节点1的值与sum相加
* 3、将节点2的值与sum相加
* 4、将sum % 10挂在新的链表中,(之所以sum%10,因为如果有进位需要将个位数挂上去,十位数进1)
* 5、sum = sum/10,得出进位,向后进1
* 6、链表循环结束后,判断最后一位相加是否进1,如果进1,要加在链表最后
*/
while (cur1!=null || cur2!=null){
if(cur1!=null){
sum += cur1.val;
cur1 = cur1.next;
}
if(cur2!=null){
sum += cur2.val;
cur2 = cur2.next;
}
cur.next = new ListNode(sum%10);
sum /= 10;
cur = cur.next;
}
if(sum==1){
cur.next = new ListNode(1);
}
return dummy.next;
}
}
/**
time:O(n) :两个链表都遍历一遍
space:O(n):每次都new一个新节点,开辟了空间
*/
3、无重复字符的最长字串(滑动窗口)
题目:给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
/**
* 输入: "abcabcbb"
* 输出: 3
* 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
*
* 输入: "bbbbb"
* 输出: 1
* 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
*/
1、思路
使用滑动窗口算法:
1、定义两个指针start 和end:start代表不重复字符子串的起点,end不断向下一个窗口滑动
2、当end遇到子串中的重复字符时,就让start指向map中该重复字符的下一个字符,就是将那个重复字符以及它前面的字符都扔掉,让窗口继续向下滑动,寻找更长的字串。
3、注意:对于HashMap有一个特点,键相同,值覆盖。
2、代码
public class Solution {
public int lengthOfLongestSubstring(String s) {
if(s.length()==0 || s==null){
return 0;
}
//定义HashMap去重:键相同,值覆盖
HashMap<Character,Integer> map = new HashMap<>();
int length = s.length();
int res = 0;
//start指向不重复字符子串的起始位置,end不断向窗口后面移动
for(int start=0,end=0;end<length;end++){
//当map中包含end指向的字符时,那就从start指向map中重复字符的下一个字符
//就是将窗口向下移动,将map中和end指向的字符重复的字符以及它之前的字符从窗口中移出。
if(map.containsKey(s.charAt(end))){
start = Math.max(start,map.get(s.charAt(end))+1);
}
//将end指向的字符添加进map,键相同值覆盖
map.put(s.charAt(end),end);
res = Math.max(res,end-start+1);
}
return res;
}
/**
time:O(n)
space:O(n)
*/
4、寻找两个正序数组的中位数(二分法,重要!)
题目:给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出这两个正序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。你可以假设 nums1 和 nums2 不会同时为空。
/**
* 示例 1:
*
* nums1 = [1, 3]
* nums2 = [2]
*
* 则中位数是 2.0
*
* nums1 = [1, 2]
* nums2 = [3, 4]
*
* 则中位数是 (2 + 3)/2 = 2.5
*/
1、思路:
1、先复习一下二分查找算法:
假设在 [left, right] 范围内搜索某个元素 value, mid == (left+ right) / 2
◼ 如果 value < mid,去 [left, mid-1] 范围内二分搜索
◼ 如果 value > mid,去 [mid + 1, right]范围内二分搜索
◼ 如果 value == mid,直接返回 mid
public static int binarySearch(int[] arr,int value){
int left = 0;
int right = arr.length-1;
while(left<=right){
int mid = (left+right) >> 1;
if(value<arr[mid]){
right = mid-1;
}else if(value>arr[mid]){
left = mid+1;
}else{
return mid;
}
}
return -1;
}
2、本题思路:
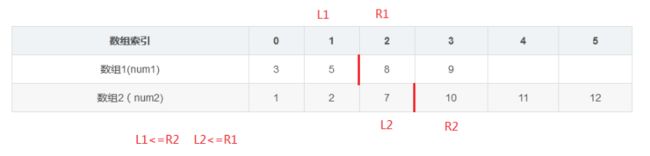
其中,N1=4,N2=6,size=4+6=10.
1、现在有的是两个已经排好序的数组,结果是要找出这两个数组中间的数值,如果两个数组的元素个数为偶数,则输出的是中间两个元素的平均值。
2、可以想象,如果将数组1随便切一刀(如在3和5之间切一刀),数组1将分成两份,数组1左别的元素个数为1,右边的元素的个数为3。
由于数组1和数组2最终分成的左右两份的个数是确定的,都是所有元素的个数的一半(size/2=5)所以我们也可以知道,此时对数组2应该切的一刀的位置应该在10和11之间,数组2左边的个数为4,右边的个数为2.才能使两个数组左右两边的元素个数加起来的和(1+4=2+3)相等。
另外,我们记在数组1靠近这一刀的左别的元素为L1(3),右边元素为R1(5).同理,记在数组2靠近这一刀的左别的元素为L2(10),右边元素为R2(11).
如果这一刀的位置是正确的,则应该有的结果是
L1<=R2
L2<=R1
这样就能确保,左边的元素都小于右边的元素了。
3、所以,我们只需要直接找出在数组1切这一刀的正确位置就可以了。
为了减少查找次数,我们对短的数组进行二分查找。将在数组1切割的位置记为cut1,在数组2切割的位置记为cut2,cut2=(size/2)-cut1。
cut1,cut2分别表示的是数组1,数组2左边的元素的个数。
4、切这一刀的结果有三种
1)L1>R2 则cut1应该向左移,才能使数组1较多的数被分配到右边。
2)L2>R1 则cut1应该向右移,才能使数组1较多的数被分配到左边。
3)其他情况(L1<=R2 L2<=R1),cut1的位置是正确的,可以停止查找,输出结果。
5、其他说明
1)考虑到边界条件,就是cut的位置可能在边缘,就是cut1=0或者cut1=N1,cut2=0或者cut2=N2的这些情况,我们将min和max两个特殊值分别加在数组1和数组2的两端,就可以统一考虑了。还有N1个数为0的时候,直接输出结果即可。
2)为了减少查找时间,使用的是二分查找,就是cut1的位置是一半一半的查找的,实现时间只要log(N),不然就会超时。所以,我们不能只是简单地将cut1–或者cut1++,而是要记下每次cut1的区域范围,我们将cut1的范围记录下来,用[cutL,cutR]表示。一开始cut1的范围是[cutL,cutR]=[0,N1],
如果L1>R2 则cut1应该向左移,才能使数组1较多的数被分配到右边。cut1的范围就变成了[cutL,cut1-1],下次的cut1的位置就是cut1 = (cutR - cutL) / 2 + cutL;。
如果L2>R1 则cut1应该向右移,才能使数组1较多的数被分配到左边。cut1的范围就变成了[cut1+1,cutR],下次的cut1的位置就是cut1 = (cutR - cutL) / 2 + cutL;。
3)数组的元素个数和是奇数的情况下,中间的元素应该就是min(R1,R2),只需另外处理输出就可以了。
2、代码
public class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
//为了减少查找次数,对短的数组进行二分查找,查找切一刀的位置
if(nums1.length>nums2.length){
return findMedianSortedArrays(nums2,nums1);
}
//根据length计算:cut2 = length/2-cut1
int length = nums1.length+nums2.length;
//数组1刀口左边的元素的个数
int cut1 = 0;
//数组2刀口左边元素的个数
int cut2 = 0;
/**
* 时间复杂度出现了log,二分查找,需要更新二分查找的范围
* 我们要查找的是那个刀口的位置在哪:[cutR,cutL]代表刀口cut1要二分查找的范围
*/
int cutL = 0;
int cutR = nums1.length;
//进行二分查找算法:
while (cut1<=nums1.length){
cut1 = (cutR-cutL)/2 + cutL;
cut2 = length/2-cut1;
/**
* 1、求出L1(cut1左侧的元素)、R1(cut1元素)、L2(cut1左侧的元素)、R2(cut2元素)
* 2、边界条件,cut的位置可能在边缘:
cut1=0、cut1=nums1.length、cut2=0、cut2=nums2.length的情况
* 3、将min和max两个特殊值分别加在数组1和数组2的两端,就可以了
*/
double L1 = (cut1==0) ? Integer.MIN_VALUE : nums1[cut1-1];
double L2 = (cut2==0) ? Integer.MIN_VALUE : nums2[cut2-1];
double R1 = (cut1==nums1.length) ? Integer.MAX_VALUE : nums1[cut1];
double R2 = (cut2==nums2.length) ? Integer.MAX_VALUE : nums2[cut2];
//判断查找到的这个刀口是否合理,若不合理更新二分查找的范围
/**
* 注意这里并不是让cut1--/cut++:
* 1、如果L1>R2 则cut1应该向左移,才能使数组1较多的数被分配到右边。
* cut1的范围就变成了[cutL,cut1-1],下次的位置是cut1 = (cutR - cutL) / 2 + cutL
*
* 2、如果L2>R1 则cut1应该向右移,才能使数组1较多的数被分配到左边。
* cut1的范围就变成了[cut1+1,cutR],下次的位置是cut1 = (cutR - cutL) / 2 + cutL
*
* 3、cut1的位置是正确的(L1<=R2 L2<=R1),可以停止查找,输出结果。
*/
if(L1>R2){
cutR = cut1-1;
}else if(L2>R1){
cutL = cut1+1;
}else{
//如果数组的总长度为偶数
if(length%2==0){
/**
* 取出L1、L2中的最大值,这个值在两个数组排序后最靠近刀口
* 取出R1、R2中的最大值,这个值在两个数组排序后最靠近刀口
*/
L1 = (L1>L2 ? L1:L2);
R1 = (R1<R2 ? R1:R2);
return (L1+R1)/2;
}else{
//如果数组的总长度为奇数,那么中位数一定为R1、R2中的最小值
R1 = (R1 < R2 ? R1 : R2);
return R1;
}
}
}
//没有找到
return -1;
}
}
/**
time:log(min(m,n))
sapce:O(1),仅在递归时使用了一个栈空间
*/
5、最长回文子串(dp)
题目:给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
/**
* 输入: "babad"
* 输出: "bab"
* 注意: "aba" 也是一个有效答案。
*
* 输入: "cbbd"
* 输出: "bb"
*/
1、思路1(dp)
1、转移状态:设dp 为二维数组,其中dp[i][j]代表字符串s 从下标i 到下表j的子串
如果dp[i,j]是回文子串,那么dp[i,j]=true,否则dp[i,j]=false:
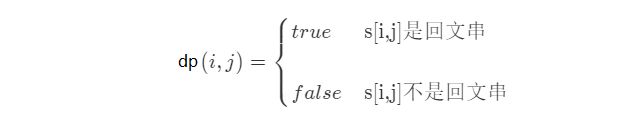
2、转移方程:dp(i, j) = (dp(i + 1, j - 1) && s[i] == s[j])
如果dp(i + 1, j - 1) 是回文子串并且s[i]==s[j],就说明是dp(i,j)回文子串

我们说对于一个题分析能不能用动态规划,不可能一下就看出转移方程了,应该怎么分析?
可以考虑从前分析确定初始条件,从后分析确定前面一步和当前步有什么关系。
(2)如果添加一个使这个字符串是回文子串它应该满足什么条件? s[i] == s[j]
(3)第n-1步如果是回文子串,怎么表示?dp(i + 1, j - 1)
3、转移边界条件:
要满足(i+1)-(j-1)>=0 即这个范围内至少要有0个字符(为0时指同一个字符,为1时代表两个字符),
才能使用dp[i-1,j+1],即j-i<2
4、返回值:s.subString(i,j+1)
2、代码1
假如说外层遍历到最后一个字符j=s.length-1
内层开始遍历,那么dp[i,j]就是判断(i,j)这段范围内的字符是否是回文子串,这样所有情况都能考虑到

class Solution {
public String longestPalindrome(String s) {
//1、进行空值判断
if(s.length()==0 || s==null){
return s;
}
//2、初始化变量
int length = s.length();
String res = "";
int max = 0;
//3、dp[i][j]代表(i,j)范围内的字符串是否是回文子串
boolean[][] dp = new boolean[length][length];
for(int j=0;j<length;j++){
//i<=j,当i=j时代表同一个字符
for(int i=0;i<=j;i++){
dp[i][j] = (s.charAt(i)==s.charAt(j)) && ((j-i<=2) || dp[i+1][j-1]);
//如果是回文子串
if(dp[i][j]){
//如果回文子串的长度>max
if(j-i+1>max){
max = j-i+1;
res = s.substring(i,j+1);
}
}
}
}
return res;
}
}
/**
* time:双层for循环,为O(n2)
* space:因为开辟了二维数组,为O(n2)
*/
3、思路2(中心扩散)
回文串一定是对称的,所以我们可以每次循环选择一个中心,进行左右扩展,判断左右字符是否相等即可。
由于存在奇数的字符串和偶数的字符串,所以我们需要从一个字符开始扩展,或者从两个字符之间开始扩展

4、代码2
很明显,代码2更好理解:
public class Solution2 {
String res = "";
public String longestPalindrome(String s) {
//1、空值判断
if(s.length()==0 || s==null) return s;
//2、遍历字符串
for(int i=0;i<s.length();i++){
//字符串的长度为奇数时,以一个为中心字符开始扩散
help(s,i,i);
//字符串的长度为偶数时,以两个字符为中心开始扩散
help(s,i,i+1);
}
return res;
}
private String help(String s, int left, int right) {
//如果判断成立,就让left向左移动,让right向右移动,向两端扩散比较是否相等
while (left>=0 && right<s.length() && s.charAt(left)==s.charAt(right)){
left--;
right++;
}
String cur = s.substring(left+1,right);
if(cur.length()>res.length()){
res = cur;
}
return res;
}
}
/**
* time:O(n2)
* space:O(1)
*/
6、Z字型变换(了解)
题目:将一个给定字符串根据给定的行数,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 “LEETCODEISHIRING” 行数为 3 时,排列如下:
1、思路
考查数学的找规律:
1、使用StringBuilder将每一行最终显示的数据拼接起来
2、
2、代码
class Solution {
public String convert(String s, int numRows) {
if(numRows < 2) return s;
//1、初始化StringBuilder
StringBuilder[] sb = new StringBuilder[numRows];
for(int i=0;i<sb.length;i++){
sb[i] = new StringBuilder("");
}
//2、通过数学规律拼接字符
for(int i=0;i<s.length();i++){
int index = i % (2* numRows-2);
index = index<numRows ? index : 2*numRows-2-index;
sb[index].append(s.charAt(i));
}
//3、将各个循环通过sb[0]拼接起来
for(int i=1;i<sb.length;i++){
sb[0].append(sb[i]);
}
return sb[0].toString();
}
}
7、整数反转(取模、求商)
题目:给出一个 32 位的有符号整数,你需要将这个整数中每位上的数字进行反转。
假设我们的环境只能存储得下 32 位的有符号整数,则其数值范围为 [−231, 231 − 1]。请根据这个假设,如果反转后整数溢出那么就返回 0。
/**
* 输入: 123
* 输出: 321
*
* 输入: -123
* 输出: -321
*
* 输入: 120
* 输出: 21
*/
1、思路
1、对于一个多位整数,使用求模+求余结合的方式取出他的每一位数:
1234:如何取出1、2、3、4 ?
4----: 1234 % 10 = 4, 1234/10=123
3----: 123 % 10 = 3, 123/10=12
2----: 12 % 10 = 2, 12/10=1
1----: 1 % 10 = 1, 1/10=0
2、取出每位数之后如何将各位数反转组合为一个新的整数?
res = 0; 每次取模的结果*10再加上下次取模的结果
1----:res = res * 10 + 1234 % 10 = 4, 1234/10=123
3----:res = res * 10 + 123 % 10 = 43, 123/10=12
2----:res = res * 10 + 12 % 10 = 432, 12/10=1
1----:res = res * 10 + 1 % 10 = 4321, 1/10=0
3、整数存储范围为是[-231,231],当x过大时,反转后result会出现溢出:
例如x=1534236469,反转后result应为9646324351,但Integer.MAX_VALUE=2147483647,导致溢出,最终result=1056389759,不是我们想要的结果,所以使用long来保存结果,判断溢出时,返回result=0。这是解决内存溢出的常用解决方案。
2、代码
class Solution {
public int reverse(int x) {
//防止整型溢出,因此使用long来保存result,判断溢出时,返回0
long res = 0;
while(x!=0){
res = res*10 + x%10;
x /= 10;
if(res>Integer.MAX_VALUE || res<Integer.MIN_VALUE){
return 0;
}
}
return (int)res;
}
}
/**
* time:O(n) 只有一个while循环
* space:O(1)
*/
8、字符串转成整数
题目:请你来实现一个 atoi 函数,使其能将字符串转换成整数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。接下来的转化规则如下:
如果第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字字符组合起来,形成一个有符号整数。
假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成一个整数。
该字符串在有效的整数部分之后也可能会存在多余的字符,那么这些字符可以被忽略,它们对函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换,即无法进行有效转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0 。
提示:
本题中的空白字符只包括空格字符 ' ' 。
假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−2^31, 2^31 − 1]。如果数值超过这个范围,请返回 INT_MAX (2^31 − 1) 或 INT_MIN (−2^31) 。
1、思路
1、首位空格:字符串前面如果有空格,使用trim()函数去除
2、只包含空格:return 0;
2、符号位:3种情况,即 ‘’+’’ , ‘‘−’’ , ''无符号",新建一个变量保存符号位,返回前判断正负。
3、数字位:
(1)将字符转换成数字:此 “数字字符的ASCII” 与 “0的ASCII相减”
(2)将字符进行拼接res = 10*res-ascii©-ascii(0);
2、代码
class Solution {
public int myAtoi(String str) {
//字符串为空
if(str.length()== 0|| str == null) return 0;
//1、使用trim()函数去除首部空格
str = str.trim();
//2、字符串仅包含空白字符时,不能转换返回0
if(str.length()==0){
return 0;
}
//符号位,初始化为1,代表是'+'
int sign = 1;
//如果是有符号位,那么start = 1,如果是无符号位start = 0;
int start = 0;
//为了防止字符串中的字符拼接起来造成内存溢出,使用long来保存结果res
long res = 0;
//3、取出字符串的第一个字符,判断符号位
char firstChar = str.charAt(0);
if(firstChar == '+'){
sign=1;
start ++;
}else if(firstChar == '-'){
sign = -1;
start++;
}
//4、遍历字符串
for(int i=start;i<str.length();i++){
//判断是否是数字
if(!Character.isDigit(str.charAt(i))){
return (int) res*sign;
}
//将字符转换为数字并拼接起来
res = res*10 + (str.charAt(i)-'0');
//判断是否内存溢出,就是结果是否超过Integer的最大值
if( sign ==1 && res>Integer.MAX_VALUE) return Integer.MAX_VALUE;
if(sign==-1 && res>Integer.MAX_VALUE) return Integer.MIN_VALUE;
}
return (int) res*sign;
}
}
/**
time:O(n)
space:O(1)
*/
9、回文数(取模、求商)
题目:判断一个整数是否是回文数。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
* 输入: 121
* 输出: true
*
* 输入: -121
* 输出: false
* 解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
*
* 输入: 10
* 输出: false
* 解释: 从右向左读, 为 01 。因此它不是一个回文数。
1、思路
由示例可以看出:
1、如果这个数时负数,一定不是回文数
2、如果这个是10、100、1000等这种类型,其最后一位是0,那么第一位也一定为0才是回文串,只有0满足
3、如果一个数时回文串,那么它反转之后应该和这个数相同,需要对这个整数进行反转:res*10+x%10,x/10
2、代码
class Solution {
public boolean isPalindrome(int x) {
//1、如果这个数时负数,或者这个数为10、100、1000等数
if(x<0 || (x%10==0 && x!=0)){
return false;
}
//2、先用一个数保存x的值
int tmp = x;
//因为没有提到内存溢出的情况,所以使用int存储即可,否则是需要使用long的
int rev = 0;
//3、对这个整数进行反转
while (x>0){
rev = rev*10 + x%10;
x /= 10;
}
//4、判断反转前后两个数是否形同
return tmp==rev;
}
}
// time:O(n)
// space :O(1)
10、正则表达式匹配(dp)
题目:给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个字符串 s的,而不是部分字符串。
说明:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
示例:
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。
输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个('*')任意字符('.')。
输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false
1、思路
使用动态规划来做,刚开始做起来感觉很难,答案都很复杂,但是想明白了也就好理解了。
dp[i][j] 表示 s 的前 i 个字符串是否能被 p 的前 j个字符串匹配。
动态规划思考的时候都是利用第n-1步来推导第n步,进而推导状态方程。
怎么想转移方程?首先想的时候从已经求出了 dp[i-1][j-1] 入手,再加上已知 s[i]、p[j],要想的问题就是怎么去求 dp[i][j]。
已知 dp[i-1][j-1] 意思就是前面子串都匹配上了,不知道新的一位的情况。
那就分情况考虑,所以对于新的一位 p[j] s[i] 的值不同,要分情况讨论:
1、假如说最后 p[j] = s[i] ,就是说新加的一位相等,那么状态仍为之前的状态:dp[i][j] = dp[i-1][j-1]
2、因为s可能为空,且只包含从 a-z 的小写字母。p可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
从 p[j] 可能的情况来考虑,让 p[j]=各种能等于的东西。
1、p[j]='.':此时p[j]可以作为任意一个字符,状态仍为之前的状态:dp[i][j] = dp[i-1][j-1]
2、p[j]='*':这各需要分情况讨论:
1、p[j-1] != s[i],让'*'前面字符消失,状态为:dp[i][j] = dp[i][j-2];
2、p[j-1] = s[i] || p[j-1] = '.'
1、假如 * 匹配前面的一个字符,dp[i][j] = dp[i][j-1]
aa ----> aa
a* ----> a
2、假如 * 匹配前面的两个字符,dp[i][j] = dp[i-1][j]
aa ----> aa
a* ----> aa (左对角线的已经相等,因此需要右对角线也相等)
3、假如'*'前面的是'.',就是'.*'可以匹配任意字符,不用考虑,因此dp[i][j] = dp[i][j-2]
说明:
'*' 的含义是 匹配零个或多个前面的那一个元素,所以要考虑他前面的元素 p[j-1]。
'*' 跟着他前一个字符走,前一个能匹配上 s[i],* 才能有用,
前一个都不能匹配上 s[i],* 也无能为力,只能让前一个字符消失,也就是匹配 0次前一个字符
2、代码
public class Solution {
public boolean isMatch(String s, String p) {
/**
* dp[i][j] 表示 s 的前 i 个字符串是否能被 p 的前 j 个字符串匹配。
*/
boolean[][] dp = new boolean[s.length()+1][p.length()+1];
//初始化dp[0][0],不存放任何数据
dp[0][0] = true;
//ab---'c*ab':c*删除,这种情况后面无法考虑因此需要先处理这种情况
for(int i=0;i<p.length();i++){
if(p.charAt(i)=='*' && dp[0][i-1] ){
dp[0][i+1] = true;
}
}
for(int i=0;i<s.length();i++){
for(int j=0;j<p.length();j++){
//p,s新增加的一位字符相等,那就不用考虑了,直接等于上一个状态
if(p.charAt(j) == s.charAt(i)){
dp[i+1][j+1] = dp[i][j];
}
//p新增的一位字符为'.',那么可以为任意字符,直接等于上一个状态
if(p.charAt(j) == '.'){
dp[i+1][j+1] = dp[i][j];
}
//p新增的一位字符为'*' 分情况考虑:
if(p.charAt(j) == '*'){
//1、如果'*'的前一个字符不等于s[i],'*'匹配0个前一个字符,将前一个字符消除掉
if(p.charAt(j-1) != s.charAt(i) && p.charAt(j-1)!='.'){
dp[i+1][j+1] = dp[i+1][j-1];
}else {
//2、如果'*'的前一个字符等于s[i],分情况考虑:
//如果*匹配一个前一个字符
//如果*匹配两个前一个字符
//如果*的前一个字符为'.'
dp[i+1][j+1] = dp[i+1][j] || dp[i][j+1] || dp[i+1][j-1];
}
}
}
}
return dp[s.length()][p.length()];
}
}
/**
* time:O(n^2) 双层for循环
* space:O(n^2) 二维数组
*/
11、盛最多水的容器(双指针)
**题目:**给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49
1、思路:
分治法、动态规划都用不上,要想得到 O(n)的解法只有使用双指针一条路。双指针法平时遇到过,但是自己只有用的多才能想到慢慢积累吧。
这一题的题意就是求两根柱子围起来的面积的最大值。
1、在一开始,我们考虑相距最远的两个柱子所能容纳水的面积。水的宽度是两根柱子之间的距离 ;水的高度取决于两根柱子之间较短的那个。设每一状态下水槽面积为S(i,j),(0<=iS(i,j)=min(h[i],h[j])×(j−i)。
2、在每一个状态下,无论长板或短板收窄 1格,都会导致水槽 底边宽度−1:
若向内移动长板,水槽的短板 min(h[i],h[j])不变或变小,下个水槽的面积一定小于当前水槽面积。(因为面积取决于短板)
若向内移动短板,水槽的短板 min(h[i],h[j])可能变大,因此水槽面积 S(i,j)可能增大,因此向内收窄短板就可以获取面积最大值。
2、代码:
class Solution {
public int maxArea(int[] height) {
//数组存放的值是每个柱子的高度
//定义一个变量存放两根柱子围成的面积
int area = 0;
//定义res存放柱子围成面积的最大值
int res = 0;
//定义一个指针指向最左边的柱子
int left = 0;
//定义一个指针指向最右边的柱子
int right = height.length-1;
while (left<right){
area = (right-left)*Math.min(height[left],height[right]);
res = Math.max(res,area);
if(height[left]<height[right]){
left++;
}else{
right--;
}
}
return res;
}
}
/**
time:O(n)
space:O(1)
*/
13、罗马数字转整数(哈希表)
**题目:**罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内。
1、思路:
这个题面试也考的挺多的,而且这种思想是经常用的,用HashMap来存储键值对,列出所有可能的键值对并判断
1、字符对应数字,首先将所有的组合的可能性列出,并添加到哈希表中
2、然后对字符串进行遍历,由于组合只有两种,一种是 1 个字符,一种是 2 个字符,其中 2 个字符优先于 1 个字符
3、先判断两个字符的组合在哈希表中是否存在,存在则将值取出加到结果 ans 中,并向后移2个字符。
不存在则将判断当前 1 个字符是否存在,存在则将值取出加到结果 ans 中,并向后移 1 个字符
4、返回res即可。
2、代码:
public int romanToInt(String s) {
HashMap<String,Integer> map = new HashMap<>();
//向哈希表中存放数据的时候,值一定要从小到大存入,否则会报空指针异常
map.put("I", 1);
map.put("IV", 4);
map.put("V", 5);
map.put("IX", 9);
map.put("X", 10);
map.put("XL", 40);
map.put("L", 50);
map.put("XC", 90);
map.put("C", 100);
map.put("CD", 400);
map.put("D", 500);
map.put("CM", 900);
map.put("M", 1000);
int res = 0;
//遍历字符串
for(int i=0;i<s.length();){
//截取字符串中的两个字符,判断是否在map中存在,如果存在就取出对应的值
if(i+1<s.length() && map.containsKey(s.substring(i,i+2))){
res += map.get(s.substring(i, i + 2));
i+=2;
}else{
//否则就截取一个字符,取出对应的值
res += map.get(s.substring(i,i+1));
i++;
}
}
return res;
}
}
14、最长公共前缀(字符串)
**题目:**编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入: ["flower","flow","flight"]
输出: "fl"
示例 2:
输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。
1、思路:
先来看indexOf()函数的用法:
- public int indexOf(int ch): 返回指定字符在字符串中第一次出现处的索引,如果此字符串中没有这样的字符,则返回 -1。
- int indexOf(String str): 返回指定字符串在字符串中第一次出现处的索引,如果此字符串中没有这样的字符串,则返回 -1。
public class Test {
public static void main(String args[]) {
String Str = new String("www.runoob.com");
String SubStr1 = new String("runoob");
String SubStr2 = new String("com");
System.out.print("查找字符 o 第一次出现的位置 :" );
System.out.println(Str.indexOf( 'o' ));
System.out.print("子字符串 SubStr1 在 str 中第一次出现的位置:" );
System.out.println(Str.indexOf( SubStr1 )); //4
System.out.print("子字符串 SubStr2 在 str 中第一次出现的位置 :" );
System.out.println(Str.indexOf( SubStr2 )); //11
}
}
注意这儿是求最长公共前缀,也就是说这些字符串的前缀是相同的。如果子串在字符串中返回结果一定为0
2、代码:
class Solution {
public String longestCommonPrefix(String[] strs) {
if(strs==null || strs.length==0){
return "";
}
//假设第一个字符串就是最长公共前缀
String res = strs[0];
//遍历字符串数组
for(int i=1;i<strs.length;i++){
//最长公共前缀子串res如果找到了,一定在strs[i]的起始位置,就是index=0的位置
//如果没有找到就不为0
while (strs[i].indexOf(res) !=0 ){
res = res.substring(0,res.length()-1);
}
}
return res;
}
}
15、三数之和(数组–双指针)
**题目:**给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
1、思路:
1、首先对数组进行排序,排序后固定一个数 nums[i],再使用左右指针指向 nums[i]后面的两端,数字分别为 nums[L] 和 nums[R],计算三个数的和 sum判断是否满足为 0,满足则添加进结果集
2、如果 nums[i] == nums[i−1],则说明该数字重复,会导致结果重复,跳过
3、当 sum== 0 时,nums[L] == nums[L+1] 则会导致结果重复,应该跳过,L++
当 sum == 0 时,nums[R] == nums[R−1]则会导致结果重复,应该跳过,R−−4、时间复杂度:O(n^2),n为数组长度
2、代码:
class Solution {
public static List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> ans = new ArrayList();
//先排序,排序后可以去重
Arrays.sort(nums);
//固定三个数中的一个数,nums[i]
for (int i = 0; i < nums.length ; i++) {
//如果nums[i]==nums[i-1] ,说明重复,跳过nums[i-1]
if(i > 0 && nums[i] == nums[i-1]) continue; // 去重
//定义左右指针,分别指向nums[i]后面数的两端
int L = i+1;
int R = nums.length-1;
//遍历,判断三数之和
while(L < R){
int sum = nums[i] + nums[L] + nums[R];
if(sum == 0){
ans.add(Arrays.asList(nums[i],nums[L],nums[R]));
while (L<R && nums[L] == nums[L+1]) L++; // 去重
while (L<R && nums[R] == nums[R-1]) R--; // 去重
L++;
R--;
} else if (sum < 0) {
L++;
} else if (sum > 0) {
R--;
}
}
}
return ans;
}
}
16、最接近的三数之和(数组–双指针)
**题目:**给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
例如,给定数组 nums = [-1,2,1,-4], 和 target = 1.
与 target 最接近的三个数的和为 2. (-1 + 2 + 1 = 2).
1、思路:
本题和上一题基本差不多:
本题目因为要计算三个数,如果靠暴力枚举的话时间复杂度会到 O(n3),需要降低时间复杂度
0、首先进行数组排序,时间复杂度 O(nlogn)
1、在数组 nums 中,进行遍历,每遍历一个值利用其下标i,形成一个固定值 nums[i]
2、再使用前指针指向 start = i + 1 处,后指针指向 end = nums.length - 1 处,也就是结尾处
3、根据 sum = nums[i] + nums[start] + nums[end] 的结果,判断 sum 与目标 target 的距离,如果更近则更新结果 res
4、同时判断 sum 与 target 的大小关系,因为数组有序,如果 sum > target 则 end–,如果 sum < target 则 start++,如果 sum == target 则说明距离为 0 直接返回结果整个遍历过程,固定值为 n 次,双指针为 n 次,时间复杂度为O(n^2)
总时间复杂度:O(nlogn) + O(n^2) = O(n^2)
2、代码:
public class Solution {
public int threeSumClosest(int[] nums, int target) {
//初始化一个res
int res = nums[0]+nums[1]+nums[2];
//对数组进行排序
Arrays.sort(nums);
//遍历nums,固定一个nums[i]
for(int i=0;i<nums.length;i++){
int left = i+1;
int right = nums.length-1;
while(left<right) {
int sum = nums[i] + nums[left] + nums[right];
if (sum < target) {
left++;
} else {
right--;
}
//判断sum和res谁更接近target
if (Math.abs(target - sum) < Math.abs(target - res)) {
res = sum;
}
}
}
return res;
}
}
18、四数之和(数组–双指针)
**题目:**给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:答案中不可以包含重复的四元组。
示例:
给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。
满足要求的四元组集合为:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
1、思路:
和三数之和解法相同,没什么大的区别,不同的是,三数之和需要固定一个数,然后使用左右指针,但是四数之和需要固定两个数然后使用左右指针。
2、代码:
public class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> list = new ArrayList<>();
if(nums.length<4) return list;
//对数组进行排序
Arrays.sort(nums);
//遍历数组,固定一个数
for(int i=0;i<nums.length;i++){
//需要去重
if(i>0 && nums[i] == nums[i-1]) continue;
for(int j=i+1;j<nums.length-1;j++){
//需要去重
if(j>i+1 && nums[j]== nums[j-1]) continue;
//定义左指针
int left=j+1;
//定义右指针
int right = nums.length-1;
while (left<right){
int sum = nums[i]+nums[j]+nums[left]+nums[right];
if(sum==target){
list.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right]));
//去重
while (left<right && nums[left]==nums[left+1]) left++;
while (left<right && nums[right]==nums[right-1]) right--;
left++;
right--;
}else if(sum<target){
left++;
}else{
right--;
}
}
}
}
return list;
}
}
/**
* time:O(n^3)+O(nlogn)=O(n^3)
* time:O(n)
*/
19、 删除链表的倒数第N个节点(快慢指针)
**题目:**给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
1、思路:
整体思路是让前面的指针先移动n步,之后前后指针共同移动直到前面的指针到尾部为止
1、首先设立预先指针dummy
2、设预先指针dummy 的下一个节点指向 head,设前指针为 fast,后指针为 slow,二者都等于dummy
3、fast 先向前移动n步,之后 fast 和 slow 共同向前移动,此时二者的距离为 n,当 fast到尾部时,slow 的位置恰好为倒数第 n 个节点
4、因为要删除该节点,所以要移动到该节点的前一个才能删除,所以循环结束条件为 fast.next != null
5、删除后返回dummy.next,为什么不直接返回 head 呢,因为 head 有可能是被删掉的点
时间复杂度:O(n)
2、代码:
public class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
//定义一个节点dummy指向头结点,防止head被删了
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode fast = dummy;
ListNode slow = dummy;
//让快指针先走n步
for(int i=0;i<n;i++){
fast = fast.next;
}
while (fast.next!=null){
fast = fast.next;
slow = slow.next;
}
//删除slow的下一个节点,让slow.next指向slow.next.next
slow.next = slow.next.next;
return dummy.next;
}
}
20、有效的括号(栈)
**题目:**给定一个只包括 ‘(’,’)’,’{’,’}’,’[’,’]’ 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
输入: "()"
输出: true
输入: "()[]{}"
输出: true
输入: "([)]"
输出: false
输入: "{[]}"
输出: true
1、思路:
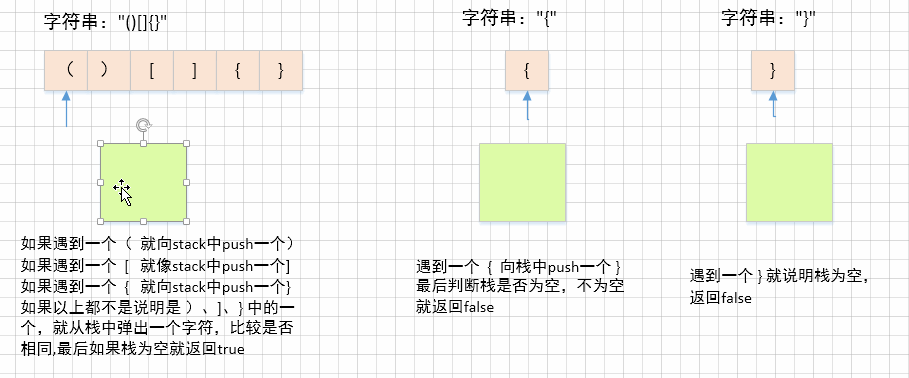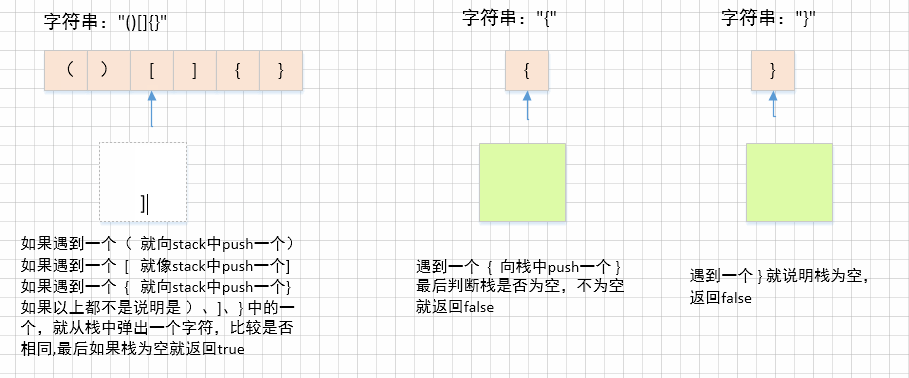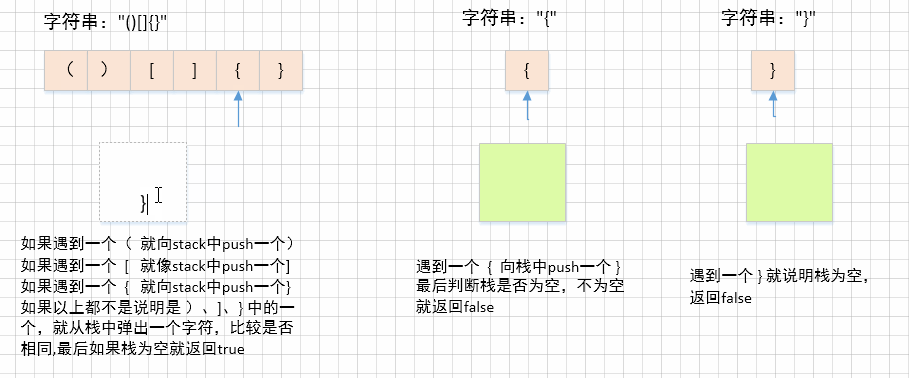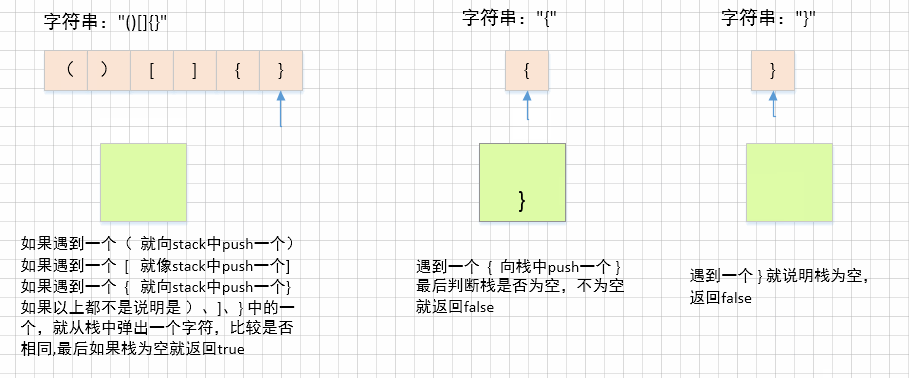
1、如果遇到
'(',就向栈中压入')'2、如果遇到
'[',就向栈中压入']'3、如果遇到
'{',就向栈中压入'}'4、如果以上条件都不满足,说明要么是
')'要么是']'要么是'}',那就从栈中弹出一个字符看是否与该字符相同,如果不相同返回false
2、代码:
public class Solution {
public boolean isValid(String s) {
if(s.length()==0 || s==null) return true;
Stack<Character> stack = new Stack<>();
//将字符串装换为字符数组
char[] charArray = s.toCharArray();
//遍历这个字符数组
for(int i=0;i<charArray.length;i++){
if(charArray[i]=='('){
stack.push(')');
}else if(charArray[i]=='['){
stack.push(']');
}else if(charArray[i]=='{'){
stack.push('}');
}else {
//如果栈为空,返回false 或者stack.pop()!=charArray[i],返回false
if(stack.isEmpty() || stack.pop()!=charArray[i] ){
return false;
}
}
}
//最终如果栈为空,返回true
return stack.isEmpty();
}
}
21、合并两个有序链表(链表)
**题目:**将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4
1、思路:
1、使用
dummy->next来保存需要返回的头节点2、判断
l1和l2哪个更小,就新建一个节点添加到链表的尾部3、直到有一边为
null,即可将另一个链表剩余的部分都接上
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
//创建一个节点dummy指向链表的头结点
ListNode dummy = new ListNode(0);
//因为dummy节点不能移动,因此创建一个指针cur指向dummy
ListNode cur = dummy;
//遍历两个链表比较节点的值的大小
while (l1!=null && l2!=null){
if(l1.val<l2.val){
cur.next = new ListNode(l1.val);
l1 = l1.next;
}else{
cur.next = new ListNode(l2.val);
l2 = l2.next;
}
cur = cur.next;
}
if(l1!=null){
cur.next = l1;
}else{
cur.next = l2;
}
return dummy.next;
}
}
22、括号生成(递归回溯)
**题目:**数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例:
输入:n = 3
输出:[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
1、思路:
递归回溯算法,深度优先搜索
1、深度优先遍历,先递归遍历左括号,
(,((,(((2、递归的时候以
(为主,如果剩余的(的个数大于0,优先遍历(3、如果剩余的
(的个数<0,说明if()条件不满足,继续向下递归)4、如果中间出现
(的剩余的个数大于)的剩余的个数,就剪枝时间复杂度:O(n!)–O(2^n)
2、代码:
class Solution {
public List<String> generateParenthesis(int n) {
List<String> list = new ArrayList<>();
if(n==0) return list;
dfs(list,"",n,n);
return list;
}
/**
* 深度优先搜索
* @param list 存放结果的集合
* @param s 拼接结果的字符串
* @param left 左括号剩余的个数
* @param right 右括号剩余的个数
*/
private void dfs(List<String> list, String s, int left, int right) {
if(left==0 && right==0){
list.add(s);
return;
}
//剪枝
if(left>right){
return;
}
//如果左括号还有剩余就深度搜索生成 (、((、(((
if(left>0){
dfs(list,s+"(",left-1,right);
}
if(right>0){
dfs(list,s+")",left,right-1);
}
}
}
23、合并K个排序链表(链表)
**题目:**合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例:
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6
1、思路:
在讲思路之前,需要去学习下如何使用优先队列并通过自定义排序规则排序:
优先级队列的元素按照其自然顺序进行排序,或者根据构造队列时提供的 Comparator 进行排序,具体取决于所使用的构造方法。
public class Student {
private String name; //名字
private int score; //分数
//省略getter/setter/构造方法...
}
public class App {
public static void main(String[] args) {
/**
* PriorityQueue:优先队列,默认按照从小到大的顺序排序
*
* 也通过实现Comparator接口指定排序规则
*/
PriorityQueue<Student> q = new PriorityQueue<Student>(new Comparator<Student>() {
/**
* 这个compare方法很容易搞混
* 如果返回1,就代表前者o1的权重大,排序默认按照从小到大的权重排,所以排序:o2 o1
* 如果返回-1,就代表后者o2的权重大,排序:o1 o2
* @param o1
* @param o2
*/
public int compare(Student o1, Student o2) {
//按照分数低到高
return o1.getScore() - o2.getScore();
}
});
//入列
q.offer(new Student("dafei", 20));
q.offer(new Student("will", 17));
q.offer(new Student("setf", 30));
q.offer(new Student("bunny", 22));
//出列
System.out.println(q.poll().getScore()); //17
System.out.println(q.poll().getScore()); //20
System.out.println(q.poll().getScore()); //22
System.out.println(q.poll().getScore()); //30
}
}
下面就打算使用优先队列来合并K个排序链表:
1、定义优先队列并实现Comparator接口,自定义排序规则:比较链表的头结点的值的大小进行排序
2、将K个排序链表加入到优先队列中
3、定义一个dummy节点指向头节点,由于dummy节点不能移动,需定义一个Cur指向dummy
4、如果队列不为空就将链表弹出,让cur.next=queue.poll(),cur = cur.next
5、同时需要将cur.next指向的节点放入队列继续进行排序。
2、代码:
/**
time:O(nlogk)
space:O(n)
*/
public class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if(lists==null) return null;
ListNode dummy = new ListNode(0);
ListNode cur = dummy;
//按照自定义排序规则创建一个优先队列
PriorityQueue<ListNode> queue = new PriorityQueue<>(new Comparator<ListNode>() {
//按照链表的头结点的大小升序排序
@Override
public int compare(ListNode o1, ListNode o2) {
//2-3=-1,说明3的权重大,3排在后面:2、3
return o1.val-o2.val;
}
});
//把K个有序链表放入队列中,放入之后会按照头节点大小从小到大排序
for(ListNode list :lists){
if(list!=null){
queue.offer(list);
}
}
//遍历这个队列
while (!queue.isEmpty()){
cur.next = queue.poll();
cur = cur.next;
//如果链表后面还有数,要将后面的数放入队列继续比较排序
if(cur.next!=null){
queue.offer(cur.next);
}
}
return dummy.next;
}
}
26、删除排序数组中的重复项(双指针)
**题目:**给定一个排序数组,你需要在 原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定数组 nums = [1,1,2],
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。
1、思路:
1、使用双指针count、i
2、开始让count=1、i=1因为nums数组中的第一个数一定是保留的,我们只需要才能够第二个数开始即可
3、如果nums[i-1]=nums[i],将nums[count++] = nums[i]
4、最后count的大小就是数组的长度
/**
* time : O(n)
* space:O(1)
*/
public class Solution {
public int removeDuplicates(int[] nums) {
if(nums.length==0 || nums==null) return 0;
//定义一个count指针,用来执行nums数组的下标,nums[0]一定是保留的,因此count=1
int count =1;
for(int i=1;i<nums.length;i++){
//如果nums[i]!=nums[i-1],就将nums[count] = nums[i]
if(nums[i] != nums[i-1]){
nums[count++] = nums[i];
}
}
return count;
}
}
27、移除元素(双指针)
**题目:**给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
给定 nums = [3,2,2,3], val = 3,
函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,1,2,2,3,0,4,2], val = 2,
函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。
注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
1、思路:
2、代码:
class Solution {
public int removeElement(int[] nums, int val) {
if(nums.length == 0) return 0;
int count =0;
for(int i=0;i<nums.length;i++){
if(nums[i] != val){
nums[count] = nums[i];
count++;
}
}
return count;
}
}
28、实现 strStr() 函数
题目:给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例 1:
输入: haystack = "hello", needle = "ll"
输出: 2
示例 2:
输入: haystack = "aaaaa", needle = "bba"
输出: -1
说明:
当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。
代码:
public class Solution {
public int strStr(String haystack, String needle) {
for(int i=0;i<=haystack.length()-needle.length();i++){
if(haystack.substring(i,i+needle.length()).equals(needle)){
return i;
}
}
return -1;
}
}
29、两数相除
**题目:**给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。返回被除数 dividend 除以除数 divisor 得到的商。整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2
示例 1:
输入: dividend = 10, divisor = 3
输出: 3
解释: 10/3 = truncate(3.33333..) = truncate(3) = 3
示例 2:
输入: dividend = 7, divisor = -3
输出: -2
解释: 7/-3 = truncate(-2.33333..) = -2
提示:
被除数和除数均为 32 位有符号整数。
除数不为 0。
假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−231, 231 − 1]。本题中,如果除法结果溢出,则返回 231 − 1。
代码:
public class Solution {
public int divide(int dividend, int divisor) {
//1、对于数值运算需要考虑正负号问题
int sign = 1;
if(dividend<0 && divisor>0 || dividend>0 && divisor<0) sign=-1;
//2、因为除数和被除数均为32位正数,并且只能存储32位有符号正数,需要考虑越界问题,使用long类型存储
long ldividend = Math.abs((long)dividend);
long ldivisor = Math.abs((long)divisor);
//3、考虑被除数<除数,被除数<0的情况
if(ldividend<ldivisor || ldividend==0) return 0;
//4、计算结果
long lres = divide(ldividend,ldivisor);
int res = 0;
if(lres>Integer.MAX_VALUE){
res = (sign==1) ? Integer.MAX_VALUE:Integer.MIN_VALUE;
}else{
res = (int)(sign*lres);
}
return res;
}
public long divide(long ldividend,long ldivisor){
if(ldividend<ldivisor) return 0;
long sum = ldivisor;
long multiply = 1;
while ((sum+sum) <= ldividend){
sum += sum;
multiply += multiply;
}
return multiply + divide(ldividend-sum,ldivisor);
}
}
30、串联所有单词的子串(滑动窗口)
**题目:**给定一个字符串 s 和一些长度相同的单词 words。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。注意子串要与 words 中的单词完全匹配,中间不能有其他字符,但不需要考虑 words 中单词串联的顺序。
示例 1:
输入:
s = "barfoothefoobarman",
words = ["foo","bar"]
输出:[0,9]
解释:
从索引 0 和 9 开始的子串分别是 "barfoo" 和 "foobar" 。
输出的顺序不重要, [9,0] 也是有效答案。
示例 2:
输入:
s = "wordgoodgoodgoodbestword",
words = ["word","good","best","word"]
输出:[]
思路:
代码:
public class Solution {
public List<Integer> findSubstring(String s, String[] words) {
List<Integer> list = new ArrayList<>();
if(s==null || words==null ||s.length()==0 || words.length==0) return new ArrayList<>();
int n = words.length;
int m = words[0].length();
HashMap<String,Integer> map = new HashMap<>();
//键存放字符串,值存放字符串出现拿的次数
for(String s1:words){
map.put(s1,map.getOrDefault(s1,0)+1);
}
for(int i=0;i<=s.length()-n*m;i++){
//将map复制一份
HashMap<String,Integer> copy = new HashMap<>(map);
//字符串的长度
int k = n;
//遍历字符串的指针
int j = i;
while (k>0){
String str = s.substring(j, j + m);
if(!copy.containsKey(str) || copy.get(str)<1){
break;
}
//键相同,值覆盖
copy.put(str,copy.get(str)-1);
j+=m;
k--;
}
if(k==0){
list.add(i);
}
}
return list;
}
}