PageRank算法详解
搜索引擎的主要工作,是爬虫建立资料库,根据关键词快速查找(倒排索引)含有关键词的页面,将结果按照重要程度排序后呈现给用户。核心难题在于如何对海量检索结果排序(Rank, Not Sort)。
1. PageRank和HITS
互联网的超链接(hyperlink)构成了一个巨大的有向图,图中的结点代表网页,有向连接表示超链接,称入链(inlink) 为连入某页面的、指向结点的超链接,而出链(outlink) 就是结点出发的超链接。
可以将超链接视为一种推荐,由我的主页指向你的主页的超链接,就是我对你的HomePage的一种认可,具有更多推荐的页面肯定比只具有少数入链的页面要更重要。同时,诸如文献引用或推荐信,推荐者本身的地位也同样重要。而且,如果推荐者相当随意和慷慨,他推荐过的数量特别多,那么他的每个推荐的权重就应当相应下调。这正是PageRank基于欢迎度评分的思想:如果一个网页被其他重要的页面所指向,那它就是重要的。
HITS方法定义了枢纽(hub)和权威(authority),如果一个页面包含了许多出链,就被认为是一个枢纽网页。如果一个页面有许多入链,就称之为一个权威网页(authority)。HITS的主要论点就是:如果一个页面指向好的权威网页,那它就是一个好的枢纽网页(给予一个较高的枢纽评分);如果一个网页被好的枢纽网页所指向,那它就是个好的权威网页。
2. 简单PageRank的求和公式:
某个页面 P i P_i Pi的PageRank记为 r ( P i ) r(P_i) r(Pi),它是所有指向 P i P_i Pi的页面的PageRank之和:
r ( P i ) = ∑ P j ∈ B P i r ( P j ) ∣ P j ∣ r(P_i) = \sum\limits_{P_j \in B_{P_i}}\dfrac{r(P_j)}{|P_j|} r(Pi)=Pj∈BPi∑∣Pj∣r(Pj)
式中, B P i B_{P_i} BPi为指向 P i P_i Pi的页面集合(就是回连至 B P i B_{P_i} BPi),而** ∣ P j ∣ |P_j| ∣Pj∣是由 P j P_j Pj发出的出链数量**。
由于入链至页面 P i P_i Pi的那些页面的PageRank值 r ( P j ) r(P_j) r(Pj)是未知的,可以用迭代的方法来绕开这个问题:假设在开始时,
所有页面都具有相等的PageRank值: 1 n \frac{1}{n} n1,n为所有页面的总数。将前一次循环中的值代入 r ( P j ) r(P_j) r(Pj),不断迭代,直到PageRank得分最终收敛到某些稳定值。
具有6个页面的网络有向图,如图所示:
假设有四个页面的有向图结构如下:
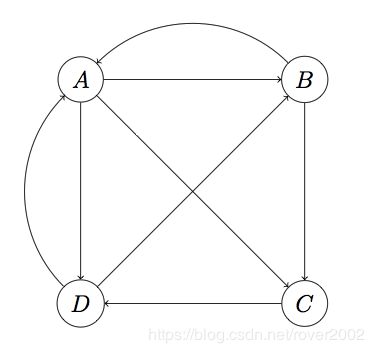
上图中A页面链向B、C、D,所以一个用户从A跳转到B、C、D的概率各为1/3。设一共有N个网页,则可以组织这样一个N维矩阵:其中i行j列的值表示用户从页面j转到页面i的概率。这样一个矩阵叫做转移矩阵(Transition Matrix)。下面的转移矩阵M对应上图:
M = [ 0 1 / 2 0 1 / 2 1 / 3 0 0 1 / 2 1 / 3 1 / 2 0 0 1 / 3 0 1 0 ] \large M=\begin{bmatrix} 0 & 1/2 & 0 & 1/2\\ 1/3 & 0 & 0 & 1/2\\ 1/3 & 1/2 & 0 & 0\\ 1/3 & 0 & 1 & 0 \end{bmatrix} M=⎣⎢⎢⎢⎡01/31/31/31/201/2000011/21/200⎦⎥⎥⎥⎤
然后,设初始时每个页面的rank值为1/N,这里就是1/4。按A-D顺序将页面rank为向量v:
v 0 = [ 1 / 4 1 / 4 1 / 4 1 / 4 ] \large v_0=\begin{bmatrix} 1/4\\ 1/4\\ 1/4\\ 1/4 \end{bmatrix} v0=⎣⎢⎢⎢⎡1/41/41/41/4⎦⎥⎥⎥⎤
M第一行分别是A、B、C和D转移到页面A的概率,而v的第一列分别是A、B、C和D当前的rank,因此用M的第一行乘以v的第一列,所得结果就是页面A最新rank的合理估计,同理,Mv的结果就分别代表A、B、C、D新rank:
M v 0 = [ 1 / 4 5 / 24 5 / 24 1 / 3 ] \large Mv_0=\begin{bmatrix} 1/4\\ 5/24\\ 5/24\\ 1/3 \end{bmatrix} Mv0=⎣⎢⎢⎢⎡1/45/245/241/3⎦⎥⎥⎥⎤
然后用M再乘以这个新的rank向量,又会产生一个更新的rank向量。迭代这个过程,可以证明v最终会收敛,即v约等于Mv,此时计算停止。最终的v就是各个页面的pagerank值。例如上面的向量经过几步迭代后,大约收敛在(1/4, 1/4, 1/5, 1/4),这就是A、B、C、D最后的pagerank。
在讨论PageRank公式之前还要先讨论两个在实际中会遇到的问题:
1)Spider Traps问题
可以预见,如果把真实的Web组织成转移矩阵,那么这将是一个极为稀疏的矩阵,从矩阵论知识可以推断,极度稀疏的转移矩阵迭代相乘可能会使得向量v变得非常不平滑,即一些节点拥有很大的rank,而大多数节点rank值接近0。而一种叫做Spider Traps节点的存在加剧了这种不平滑。例如下图:
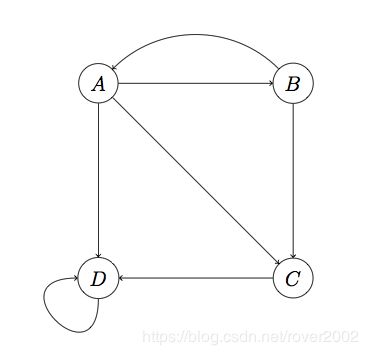
注意,D只链向自己(链向自己也算外链,当然同时也是个内链)。这种节点叫做Spider Trap,如果对这个图进行计算,会发现D的rank越来越大趋近于1,而其它节点rank值几乎归零。
2)Dead Ends问题
Dead Ends,就是这样一类节点:它们不存在外链。如下图所示:
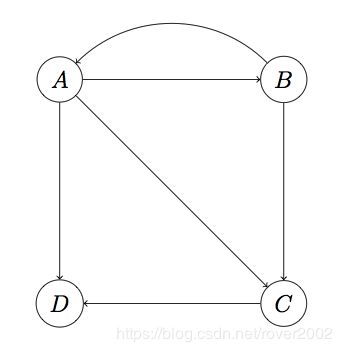
这里D页面不存在外链,是一个Dead End。上面的算法之所以能成功收敛到非零值,很大程度依赖转移矩阵这样一个性质:每列的加和为1。而在这个图中,M第四列将全为0。在没有Dead Ends的情况下,每次迭代后向量v各项的和始终保持为1,而有了Dead Ends,迭代结果将最终归零。
3. 修正后的迭代公式
为了克服这种由于矩阵稀疏性和Spider Traps带来的问题,需要对PageRank计算方法进行一个平滑处理,加入一个随机转移概率():就是我们假设在任何一个页面浏览的用户都有可能以一个极小的概率瞬间转移到另外一个随机页面。当然,这两个页面可能不存在超链接,随机转移概率只是为了算法需要而强加的一种素性调整(primitivity adjustment)。加入了随机转移概率后,每个节点向其他节点转移的概率更加倾向于“均等化”了,这就等于削弱了原本的网络结构的先验特性。它本质上就是一个结构风险最小化思想。
加入随机概率转移后,向量迭代公式变为:
v ′ = ( 1 − β ) M v + e β N \large {v}'=(1-\beta)Mv+e\frac{\beta}{N} v′=(1−β)Mv+eNβ
有的也写作:
V ′ = α M V + ( 1 − α ) e \large{V'}=\alpha MV + (1-\alpha)e V′=αMV+(1−α)e,其中e是单位矩阵,N是page总数。
另一种理解:
为了处理那些“没有外部链接的页面”(这些页面就像“黑洞”一样吞噬掉用户继续向下浏览的概率)所带来的问题,我们假设:这类页面链接到集合中所有的网页(不管它们是否相关),使得这类网页的PR值将被所有网页均分。对于这种残差概率(residual probability),我们引入阻尼系数 d(damping factor),并声明d=0.85,其意义是:任意时刻,用户访问到某页面后继续访问下一个页面的概率,相对应的1-d=0.15则是用户停止点击,随机浏览新网页的概率。d的大小由一般上网者使用浏览器书签功能的频率的平均值估算得到。
P R ( p i ) = d ∑ p j ∈ M ( p i ) P R ( p j ) L ( p j ) + 1 − d N PR(p_i)=d\sum_{p_j\in M(p_i)}\dfrac{PR(p_j)}{L(p_{j})}+{\dfrac{1-d}{N}} PR(pi)=d∑pj∈M(pi)L(pj)PR(pj)+N1−d
其中, p 1 , p 2 , … , p N p_{1},p_{2},…,p_{N} p1,p2,…,pN是目标页面, M ( p i ) M(p_{i}) M(pi)是链入 p i p_i pi页面的集合, L ( p j ) L(p_{j}) L(pj)是页面 p j p_j pj链出页面的数量,而N是所有頁面的數量。
PageRank的计算过程:
- 为每个网站设置一个初始的PageRank值。
- 第一次迭代:每个网站得到一个新的PageRank。
- 第二次迭代:用这组新的PageRank再按上述公式形成另一组新的PageRank。
- 重复迭代直至PageRank值收敛
什么时候迭代结束?
- 每个页面的PR值和上一次计算的PR相等
- 设定一个差值指标(0001)。当所有页面和上一次计算的PR差值平均小于该标准时,则收敛。
- 设定一个百分比(99%),当99%的页面和上一次计算的PR相等
- 设置最大循环次数。
4. 特性和推广应用
优点:
是一个与查询无关的静态算法,所有网页的PageRank值通过离线计算获得;有效减少在线查询时的计算量,极大降低了查询响应时间。
缺点:
- 人们的查询具有主题特征,PageRank忽略了主题相关性,导致结果的相关性和主题性降低。
- 没有区分站内导航链接,没有过滤广告链接和功能链接。功能链接常常链接到某个社交网站首页(例如常见的“分享到微博”)。
- 旧的页面等级会比新页面高。因为即使是非常好的新页面也不会有很多上游链接,除非它是某个站点的子站点。
Generalize在机器学习中是泛化的意思,也译作推广。
When To Use(适用场景):
PageRank可以应用于很多领域。以下是一些值得注意的用例:
- Twitter使用个性化PageRank向用户推荐他们可能希望关注的其他用户。该算法运行在一个包含共享兴趣和公共连接的图上。他们的方法在WTF: The Who to Follow Service at Twitter中有更详细的描述。
- PageRank被用来对公共空间或街道进行排名,预测这些区域的交通流量和人的活动。该算法在一个包含由道路连接的十字路口的图上运行,PageRank得分反映了人们在每条街道上停车或结束行程的倾向。这在论文“预测交通流的自组织自然道路:敏感性研究”中有更详细的描述。
- PageRank可以用作医疗保健和保险行业异常或欺诈检测系统的一部分。它可以帮助找到行为异常的医生或供应商,然后将PR分数输入机器学习算法。
when Not to use:
不适宜的场景比如:
- 如果一组页面中没有到组外的链接,则认为该组是一个Spider Trap。
- 当由页面组成的网络形成无限循环时,就会发生Rank Sink。
- 当页面没有外链接时,就会出现死角。如果一个页面包含到另一个没有外链接的页面的链接,这个链接将被称为悬空链接(Dangling link)。
如果您在运行算法时看到了意外的结果,那么有必要对图进行一些探索性分析,看看这些问题是否是原因。你可以阅读谷歌 PageRank算法及其工作原理 来了解更多。
Ref:
https://blog.codinglabs.org/articles/intro-to-pagerank.html
https://www.biaodianfu.com/pagerank.html
https://neo4j.com/docs/graph-algorithms/current/algorithms/page-rank/#algorithms-pagerank-personalized
补充:
spark实现pagerank算法:
package org.apache.spark.examples
import org.apache.spark.sql.SparkSession
/**
* Computes the PageRank of URLs from an input file. Input file should
* be in format of:
* URL neighbor URL
* URL neighbor URL
* URL neighbor URL
* ...
* where URL and their neighbors are separated by space(s).
*
* This is an example implementation for learning how to use Spark. For more conventional use,
* please refer to org.apache.spark.graphx.lib.PageRank
*
* Example Usage:
* {{{
* bin/run-example SparkPageRank data/mllib/pagerank_data.txt 10
* }}}
*/
object SparkPageRank {
def showWarning() {
System.err.println(
"""WARN: This is a naive implementation of PageRank and is given as an example!
|Please use the PageRank implementation found in org.apache.spark.graphx.lib.PageRank
|for more conventional use.
""".stripMargin)
}
def main(args: Array[String]) {
if (args.length < 1) {
System.err.println("Usage: SparkPageRank " )
System.exit(1)
}
showWarning()
val spark = SparkSession
.builder
.appName("SparkPageRank")
.getOrCreate()
val iters = if (args.length > 1) args(1).toInt else 10
val lines = spark.read.textFile(args(0)).rdd
val links = lines.map{ s =>
val parts = s.split("\\s+")
(parts(0), parts(1))
}.distinct().groupByKey().cache()
var ranks = links.mapValues(v => 1.0)
for (i <- 1 to iters) {
val contribs = links.join(ranks).values.flatMap{ case (urls, rank) =>
val size = urls.size
urls.map(url => (url, rank / size))
}
ranks = contribs.reduceByKey(_ + _).mapValues(0.15 + 0.85 * _)
}
val output = ranks.collect()
output.foreach(tup => println(s"${tup._1} has rank: ${tup._2} ."))
spark.stop()
}
}