面试宝典之python数据结构---列表，栈与队列，链表，树，字典

Python基本数据结构

一、线性表

线性表是最常用且最简单的一种数据结构，它是n个数据元素的有限序列。

实现线性表的方式一般有两种，一种是使用数组存储线性表的元素，即用一组连续的存储单元依次存储线性表的数据元素。另一种是使用链表存储线性表的元素，即用一组任意的存储单元存储线性表的数据元素（存储单元可以是连续的，也可以是不连续的）。

列表list

list的显著特征

• 列表中的每个元素都可变的，意味着可以对每个元素进行修改和删除
• 列表是有序的，每个元素的位置是确定的，可以用索引去访问每个元素
• 列表中的元素可以是Python中的任何对象
  可以为任意对象就意味着元素可以是字符串、整数、元组、也可以是list等Python中的对象。

x = [1,2,3]
y = {'name':'Sakura'}
z="Test"
a=[x,y,z]
a
[[1, 2, 3], {'name': 'Sakura'}, 'Test']

list中的正反索引

list中的增删查改

1. 利用insert()和分片将元素添加到指定位置 , 利用remove()和关键字del对
   元素进行删除

   需要注意分片[a:b]中的位置不包含位置b，利用[a,a]可以将元素添加至a位置

   本Markdown编辑器使用[StackEdit][6]修改而来，用它写博客，将会带来全新的体验哦：
   
   

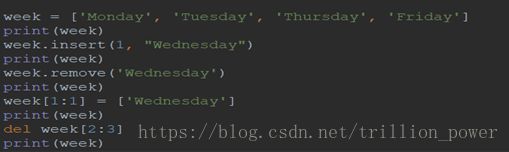
   1. 利用正反索引对元素进行查找
   2. 对元素修改可以直接赋值替换
   3. 列表中还有其他方法如pop()删除末尾元素，pop(i)删除指定位置i的元素，append()向末尾添加元素。

可以通过list将序列创建为列表
Python中包含6中內建的序列：列表，元组，字符串、Unicode字符串、buffer对象和xrange对象。

链表

链表的结构：链表像锁链一样，由一节节节点连在一起，组成一条数据链。
链表的节点的结构如下：
data next
data为自定义的数据，next为下一个节点的地址。
链表的结构为，head保存首位节点的地址：

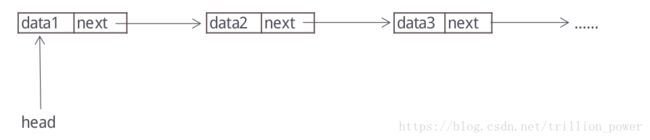
单链表

接下来我们来用python实现链表

python实现链表

首先，定义节点类Node：

class Node:
    '''
    data: 节点保存的数据
    _next: 保存下一个节点对象
    '''
    def __init__(self, data, pnext=None):
        self.data = data
        self._next = pnext

    def __repr__(self):
        '''
        用来定义Node的字符输出，
        print为输出data
        '''
        return str(self.data)

然后，定义链表类：

链表要包括：

属性：

链表头：head

链表长度：length

方法：

判断是否为空: isEmpty()

def isEmpty(self):
    return (self.length == 0

增加一个节点(在链表尾添加): append()

def append(self, dataOrNode):
    item = None
    if isinstance(dataOrNode, Node):
        item = dataOrNode
    else:
        item = Node(dataOrNode)

    if not self.head:
        self.head = item
        self.length += 1

    else:
        node = self.head
        while node._next:
            node = node._next
        node._next = item
        self.length += 1

删除一个节点: delete()

#删除一个节点之后记得要把链表长度减一
def delete_node(self, index):
    if self.isEmpty():
        print '[*]This ChainTable is Empty!'
        return

    if index < 0 or index >= self.length:
        print '[*]Error! index out of range!'
        return

    if index == 0:
        self.head = self.head._next
        self.length -= 1
        return

    j = 0
    node = self.head
    prev = self.head

    while node._next and j < index:
        prev = node
        node = node._next
        j += 1

    if j == index:
        prev._next = node._next
        self.length -= 1

    print 'Success delete a node'

修改一个节点: update()

def update(self, index, data):
    if self.isEmpty():
        print '[*]This ChainTable is Empty!'
        return

    if index < 0 or index >= self.length:
        print '[*]Error! index out of range!'
        return

    j = 0
    node = self.head
    while node._next and j < index:
        node = node._next
        j += 1

    if j == index:
        node.data = data
    print 'Success update a node'

查找一个节点: getItem()

def getitem(self, index):
    if self.isEmpty():
        print '[*]This ChainTable is Empty!'
        return
    if index < 0 or index >= self.length:
        print '[*]Error! index out of range!'
        return

    j = 0
    node = self.head
    while node._next and j < index:
        node = node._next
        j += 1

    if j == index:
        return node.data
    #print 'Success get a node value'

查找一个节点的索引: getIndex()

def getindex(self, data):
    if self.isEmpty():
        print '[*]This ChainTable is Empty!'
        return

    j = 0
    node = self.head
    while node:
        if node.data == data:
            return j
            print 'Success get index'
        node = node._next
        j += 1

    if j == self.length:
        print('%s is not found' %str(data))
        return

插入一个节点: insert()

def insert(self, index, dataOrNode):
    if index < 0 or index >= self.length:
        print '[*]Error! index out of range!'
        return

    item = None
    if isinstance(dataOrNode, Node):
        item = dataOrNode
    else:
        item = Node(dataOrNode)

    if index == 0:
        item._next = self.head
        self.head = item
        self.length += 1

    j = 0
    node = self.head
    prev = self.head
    while node._next and j < index:
        prev = node
        node = node._next
        j += 1

    if j == index:
        item._next = node
        prev._next = item
        node = item
        self.length += 1
    print 'Success insert a node'

清空链表: clear()

def clear(self):
    self.head = None
    self.length = 0

反转链表

def reverseList(self, head):
    """
    :type head: ListNode
    :rtype: ListNode
    """

    #temp = ListNode(0)
    temp = head
    cur = head
    #length = 0
    #while node.next:
        #length += 1

    prev = None
    #j = 0
    while cur:
        temp = cur
        change = cur.next
        cur.next = prev
        prev = cur
        cur = change

    node = temp
    ans = []
    while node:
        ans.append(node.val)
        node = node.next
    return ans

循环链表(环形链表)

将单链表中终端结点的指针域由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表，简称循环链表。
代码实现，输入一个单链表的头(head)构造环形链表：

def cyclechaintable(head):
    node = head
    #寻找尾节点
    while node.next:
        node = node.next
    #尾节点指向头结点
    node.next = head
    return head

将两个链表合并成循环链表
(1) 算法思想
假设有A、B两个循环链表，且其尾指针分别为rearA、rearB。

1. 使A循环链表的尾指针rearA指向(rearA->next)B循环链表的第一个结点(非头结点);
2. 使B循环链表的尾指针rearB指向(rearB->next)A循环链表的头结点，即就链接成了一个新的循环链表。

def mergetwochainable(headA, headB):
    node1 = headA
    while node1.next:
        node1 = node1.next
    node1.next = headB
    node2 = headB
    while node2.next:
        node2 = node2.next
    node2.next = headA

    return headA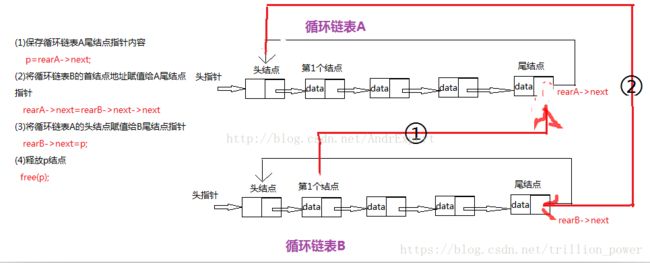    

注：循环链表和单链表的主要差异就在于循环的判断条件上，即p.next是否为空。如果最后一个结点的指针域p.next为空则说明该链表为单链表;如果p.next等于头结点则说明该链表为循环链表，假如终端结点的指针域rear，那么rear.next指向头结点。

判断单项链表是否有环

算法思路：用两个指针开始都指向头节点，pA一次移动一个节点，pB一次向后移动两个节点，循环下去……每循环一次，如果pB==NULL，说明没有环（否则不会到达NULL），结束；如果pB==pA(转回来了)，说明有环，结束。

def hasCycle(self, head):
    slow = head
    fast = head

    if head == None:
        print 'This chaintable do not has Cycle!'
        return False

    while slow:
        slow = slow.next
        fast = fast.next
        if fast and fast.next:
            fast = fast.next
        else:
            print 'This chaintable do not has Cycle!'
            return False
            break

        if slow == fast:
            print 'This chaintable has Cycle!'
            return True
            break

双向链表(感觉双向链表遇到的比较少，就简要介绍)

双向链表是在单链表的每个结点中，再设置一个指向其前驱结点的指针域。与单链表的主要区别是，双链表中的结点都有两个指针域，一个指向直接后继，另一个指向直接前驱。用空间换来时间上的性能改进。
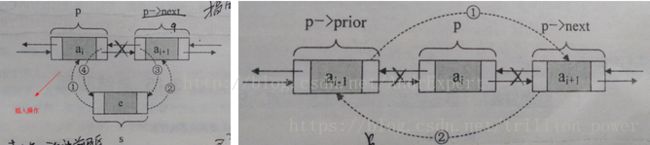
(1)插入一个元素
实现思路：
a)创建新结点s，分别设置其直接后继、直接前驱
s.prior=p;
s.next=p.next;
b)将新结点s赋值给p.next结点的直接前驱指针(p.next.prior)
p.next.prior = s;
c)将新结点s赋值p结点的直接后继指针(p.next)
p.next = s;（b.c不能互换，否则p.next.prior = p）
(2)删除一个元素
实现思路：

p->prior->next=p->next;    //把p->next赋值给p->prior的后继
p->next->prior=p->prior;    //把p->prior赋值给p->next的前驱
free(p);                                 //释放结点p占用的内存空间

栈与队列

栈和队列也是比较常见的数据结构，它们是比较特殊的线性表，因为对于栈来说，访问、插入和删除元素只能在栈顶进行，对于队列来说，元素只能从队列尾插入，从队列头访问和删除。

栈

栈是限制插入和删除只能在一个位置上进行的表，该位置是表的末端，叫作栈顶，对栈的基本操作有push(进栈)和pop(出栈)，前者相当于插入，后者相当于删除最后一个元素。栈有时又叫作LIFO(Last In First Out)表，即后进先出。

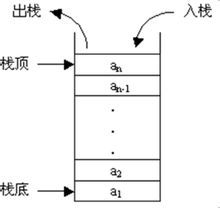
因为栈也是一个表，所以任何实现表的方法都能实现栈。我们可以用python的list 来模拟栈的相关操作如pop()，append()。

队列

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。
python队列实现：

import Queue

q = Queue.Queue()

for i in range(5):
    q.put(i)

while not q.empty():
    print q.get()

例题：用2个栈实现一个队列。
算法思想：
第一个栈临时保存插入的数据，当调用弹出函数的时候，如果stack2不为空则直接弹出；为空则把stack1中的数据全部弹出放到stack2中。

这样不会存在冲突，而且由于stack2保存的是以前的老数据，弹出一定都符合队列的规律。

# -*- coding:utf-8 -*-
class Solution:
    def __init__(self):
        self.stackA = []
        self.stackB = []

    def push(self, node):
        self.stackA.append(node)
        # write code here
        #return self.input

    def pop(self):
        # return xx
        if self.stackB:
            return self.stackB.pop()
        elif not self.stackA:
            return None
        else:
            while(self.stackA):
                self.stackB.append(self.stackA.pop())
            xx = self.stackB.pop()
            return xx

树与二叉树

树型结构是一类非常重要的非线性数据结构，其中以树和二叉树最为常用。在介绍二叉树之前，我们先简单了解一下树的相关内容。

树

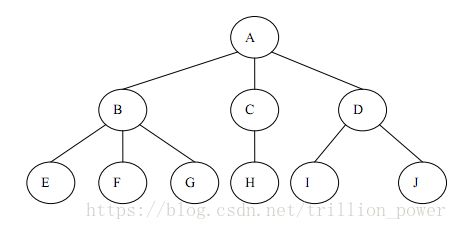
树 是由n（n>=1）个有限节点组成一个具有层次关系的集合。它具有以下特点：每个节点有零个或多个子节点；没有父节点的节点称为 根 节点；每一个非根节点有且只有一个 父节点 **；除了根节点外，每个子节点可以分为多个不相交的子树。

二叉树

定义

二叉树是每个节点最多有两棵子树的树结构。通常子树被称作“左子树”和“右子树”。二叉树常被用于实现二叉查找树和二叉堆。

相关性质

二叉树的每个结点至多只有2棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。
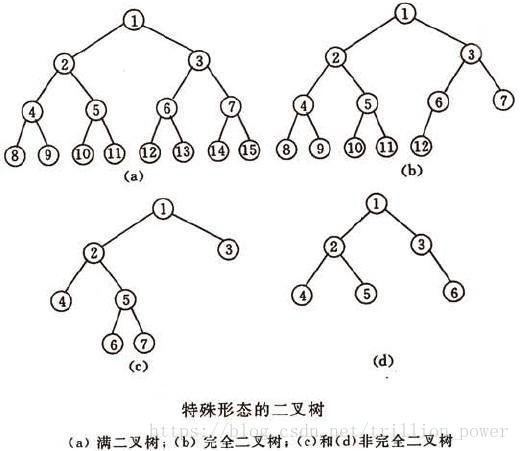
二叉树的第i层至多有 2(i−1) 2 ( i − 1 ) 个结点；深度为k的二叉树至多有 2(k−1) 2 ( k − 1 ) 个节点。一棵深度为k，且有 2k−1 2 k − 1 个节点的二叉树称之为* 满二叉树 ；深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中，序号为1至n的节点对应时，称之为 完全二叉树 *。

在二叉树的一些应用中，常常要求在树中查找具有某种特征的节点，或者对树中全部节点进行某种处理，这就涉及到二叉树的遍历。二叉树主要是由3个基本单元组成，根节点、左子树和右子树。如果限定先左后右，那么根据这三个部分遍历的顺序不同，可以分为先序遍历、中序遍历和后续遍历三种。

(1) 先序遍历 若二叉树为空，则空操作，否则先访问根节点，再先序遍历左子树，最后先序遍历右子树。 (2) 中序遍历 若二叉树为空，则空操作，否则先中序遍历左子树，再访问根节点，最后中序遍历右子树。(3) 后序遍历 若二叉树为空，则空操作，否则先后序遍历左子树访问根节点，再后序遍历右子树，最后访问根节点。

用python定义一个树结构以及3种遍历代码：

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class solution(object):
    def __init__(self):
        self.ans = []
        #self.leftdepth = 0
        #self.rightdepth = 0

    """docstring for solution"""
    # previous order traverse #
    def pretraverse(self, root):
        if root is None:
            return 
        #print root.val
        self.ans.append(root.val)
        self.pretraverse(root.left)
        self.pretraverse(root.right)

    # middle order traverse #
    def midtraverse(self, root):
        if root is None:
            return 
        self.midtraverse(root.left)
        self.ans.append(root.val)
        self.midtraverse(root.right)

    # after order traverse #
    def aftertraverse(self, root):
        if root is None:
            return 
        self.aftertraverse(root.left)
        self.aftertraverse(root.right)
        self.ans.append(root.val)

树和二叉树的区别

(1) 二叉树每个节点最多有2个子节点，树则无限制。 (2) 二叉树中节点的子树分为左子树和右子树，即使某节点只有一棵子树，也要指明该子树是左子树还是右子树，即二叉树是有序的。 (3) 树决不能为空，它至少有一个节点，而一棵二叉树可以是空的。

上面我们主要对二叉树的相关概念进行了介绍，下面我们将从二叉查找树开始，介绍二叉树的几种常见类型，同时将之前的理论部分用代码实现出来。

二叉查找树

二叉查找树就是二叉排序树，也叫二叉搜索树。二叉查找树或者是一棵空树，或者是具有下列性质的二叉树： (1) 若左子树不空，则左子树上所有结点的值均小于它的根结点的值；(2) 若右子树不空，则右子树上所有结点的值均大于它的根结点的值；(3) 左、右子树也分别为二叉排序树；(4) 没有键值相等的结点。

题目

判断二叉搜索树
算法思想：
二叉搜索树的关键是，左子树的值均小于根节点的值，右子树的值均大于根节点的值。另外要注意空节点的情况。
代码如下：

def valid(self, root, upper, lower):
    if root is None:
        return True
    if root.val <= lower or root.val >= upper:
        return False
    return self.valid(root.left, root.val, lower) and self.valid(root.right, upper, root.val)

def isValidBST(self, root):
    import sys
    return self.valid(root, float('inf'), float('-inf'))

性能分析

对于二叉查找树来说，当给定值相同但顺序不同时，所构建的二叉查找树形态是不同的，下面看一个例子。

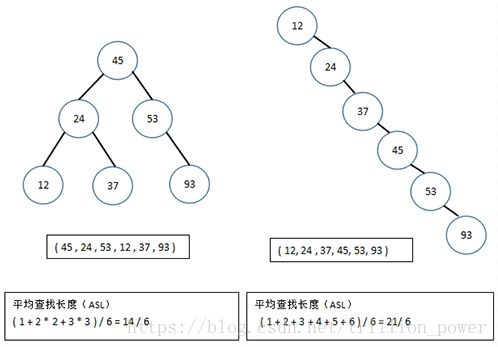
可以看到，含有n个节点的二叉查找树的平均查找长度和树的形态有关。最坏情况下，当先后插入的关键字有序时，构成的二叉查找树蜕变为单支树，树的深度为n，其平均查找长度(n+1)/2(和顺序查找相同），最好的情况是二叉查找树的形态和折半查找的判定树相同，其平均查找长度和log2(n)成正比。平均情况下，二叉查找树的平均查找长度和logn是等数量级的，所以为了获得更好的性能，通常在二叉查找树的构建过程需要进行“平衡化处理”，之后我们将介绍平衡二叉树和红黑树，这些均可以使查找树的高度为O(log(n))。

判断对称二叉树：
例如，这个二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3

但是下面这个 [1,2,2,null,3,null,3] 则不是:

1
/ \
2 2
\ \
3 3

分析：对于一棵二叉树，我们首先从根节点开始遍历

（1）如果左右子树有一个为空，那么该二叉树肯定不是对称二叉树

（2）如果左右子树均不为空，但是节点的值不同，那么该二叉树肯定不是对称二叉树

（3）如果左右子树均不空，且对应的节点值相同，那么：

     （1）遍历左子树，遍历顺序为：根->左->右

     （2）遍历右子树，遍历顺序为:   根->右->左

如果左子树序列和右子树序列一样，那么该二叉树为对称二叉树
代码如下:

def isSymmetric(self, root):
    if root is None:
        return True
    return self.symmetric(root.left, root.right)

def symmetric(self, left, right):
    if left is None and right is None:
        return True
    if left is None or right is None:
        return False
    return (left.val == right.val) and self.symmetric(left.left, right.right) and self.symmetric(left.right, right.left)

二叉树的最大深度

算法思想：
通过递归的思想，不是None深度就+1，一个用于左子树递归，一个用于右子树递归，最后获取左子树和右子树深度的最大值。
代码：

def maxdepth(self, root):
    if root is None:
        return 0

    leftdepth = self.maxdepth(root.left) + 1
    rightdepth = self.maxdepth(root.right) + 1

    return max(leftdepth, rightdepth)

二叉树的层次遍历

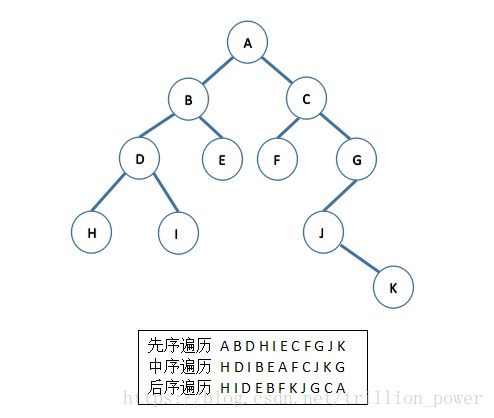
就是按照树的深度一层一层的遍历，例如

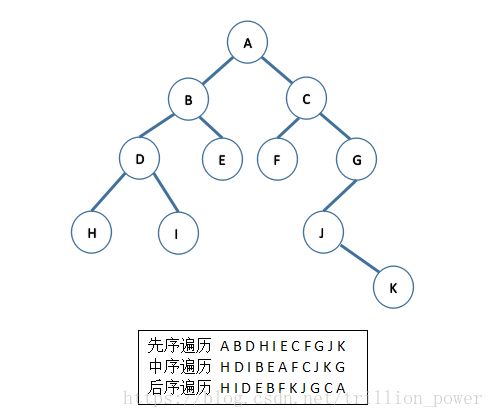
层次遍历结果为：{[A], [B,C], [D,E,F,G], [H,I,J], [K]}
算法思想：求出二叉树最大深度，在求出每一个节点的所在层数，遍历所有层，把每一层节点打印
代码如下：

class Solution(object):
    def levelOrder(self, root):
        ans = []
        depth = self.maxdepth(root)
        if root is None:
            return ans
        #遍历每一层
        for i in range(1, depth+1):
            self.levelnode(i, root, ans)
        return ans

    def maxdepth(self, root):
        if root is None:
            return 0
        leftdepth = self.maxdepth(root.left) + 1
        rightdepth = self.maxdepth(root.right) + 1

        return max(leftdepth, rightdepth)

    #打印该层的所有节点
    def levelnode(self, level, root, ans):
        if root is None or level < 1:
            ans.append(None)
            return 
        if level == 1:
            print root.val
            ans.append(root.val)
            return 
        self.levelnode(level-1, root.left, ans)
        self.levelnode(level-1, root.right, ans)

字典

一种能极大提高查找效率的数据结构。

　　映射（mapping）：通过名字来引用值的数据结构。

　　字典是Python中唯一内建的映射类型。字典的键值对（Key-Values），键是不可变的，可以为字符串、数字（int、float……）、元组等等。

　　字典中的键是唯一的，而值却可以相同。

Python格式如下：

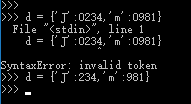
phone = {'Jack':'0571','James':'7856','Paul':'2364'} #大括号，且键值对之间用冒号（:）隔开

注：对于上面的代码，可能有读者会疑问：为什么用字符串表示电话号码呢？

　　主要是考虑以“0”开头的电话号码。定义电话号码时，以“0”开头会显示错误（Error）。因此，为了考虑周全，字典中电话号码应表示为数字字符串，而不是整数。

创建字典和访问元素

创建方式如下：

d = {'a':'97','b':'98','c':'99','c':'101'}
print(d)
d['a']
'97'

注：字典中即使键相同，也只会输出其中一个（若Key相同，后面的值（Value）会把前面的覆盖掉）。

添加元素

字典没有insert()方法，但依然能够添加元素。直接添加索引和值

d = {'a':'98','b':'99','c':'100'}
d['d'] = '101'
print(d)

删除元素

字典中删除元素，使用pop()方法。pop()方法用于获得对应于给定键的值，并将该键值对从字典中移除。

d ={‘a':'97','b':'98','c':'99'}
d.pop('b')
'98'
print(d)
{‘a':'97','c':'99'}

注：除了pop()方法，还可以使用del方法

del dict['Name']; # 删除键是'Name'的条目
dict.clear();     # 清空词典所有条目

修改元素

字典中的元素如何修改呢？很简单，直接通过Key修改Value。

d ={‘a':'97','b':'98','c':'99'}
d['b'] = '200'
print(d['b'])
'200'
print(d)
d ={‘a':'97','b':'200','c':'99'}

查找元素

字典中查找元素与修改元素类似，也是通过Key来查找字典中的Value。

d ={‘a':'97','b':'98','c':'99'}
d['b']
'98'
d['c']
'99'

如果字典中没有该Key时，dict会报错。

判断Key是否在dict中：

‘a’ in d
True
'f' in d
False

get()方法用于更宽松的访问字典项的方法。如果Key不存在，使用get()没有任何异常，仅仅返回None值：

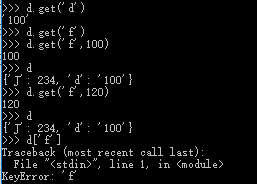
字典基本操作总结

  ♦len(d)：返回d中键-值对的数量；

  ♦d[k]：返回关联到键K上的值（Value）；

  ♦d[k] = V：将值V关联到将K上；

  ♦del d[k]：删除键为K的项；

  ♦K in d：检查d中是否含有键K的元素；

  ♦键K类型：字符串、数字或元组，符合条件的不可变类型均可；

  ♦字典格式化字符串：%(Jack)s %(phone)。【其中Jack为键，而phone为dict{}】

　　1.字典中元素必须以键值对的形式出现；

　　2.字典中的键必须是不可变的，可以是字符串、数字以及元组，并且无法修改；

　　3.Key是唯一的，不可重复，而Value可以重复；

　　4.字典查找和插入元素极快，并不会随着Key增加而减慢；

　　5.字典占用内存大，以空间换取时间；

　　6.特别地，当tuple作为字典中的键（Key）时，tuple中不能包含list，否则编译错误。

dict中的散列表

• 散列表算法
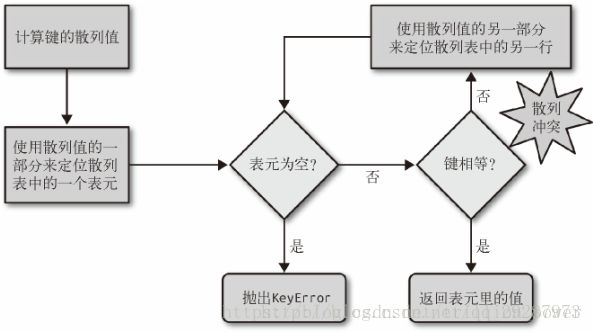
  正常想要获取dict中的值，首先要知道key通过dict[key]获取对应的value，在散列表中为了达到这种操作，首先会计算key的hash值即散列值，把这个值最低的几位数字当作偏移量，在散列表里
  查找表元（具体取几位，得看当前散列表的大小）。若找到表元为空，异常KeyError，不为空，表元里会有一对 found_key:found_value。这时候 Python 会检验 search_key == found_key 是否为真，如果它们相等的话，就会返回 found_value。如果两个值不匹配，则是散列冲突。

而散列表本
身的索引又只依赖于这个数字的一部分。为了解决散列冲突，算法会在散列值中另外
再取几位，然后用特殊的方法处理一下，把新得到的数字再当作索引来寻找表元。
若这次找到的表元是空的，则同样抛出 KeyError；若非空，或者键匹配，则返回这
个值；或者又发现了散列冲突，则重复以上的步骤。

另外在插入新值时，Python 可能会按照散列表的拥挤程度来决定是否要重新分配内存
为它扩容。如果增加了散列表的大小，那散列值所占的位数和用作索引的位数都会随
之增加，这样做的目的是为了减少发生散列冲突的概率。

Python 会设法保证大概还有三分之一的表元是空的，所以在快要达到这个阈值的时
候，原有的散列表会被复制到一个更大的空间里面。

• dict的散列实现导致的结果
  1.key必须是可hash的，所有不可变类型都是可哈希的故可作为键，可变类型不可哈希即不可作为键，如列表，字典类型。

  2.在内存消耗上是巨大的，由于字典使用了散列表，而散列表又必须是稀疏的，这导致它在空间上的效率低下。

  3.key查询很快，hash表空间换时间。

  4.key的排列顺序，取决于添加顺序，并且当dict添加新数据，原有的排列可能会被打乱，因为Python 会设法保证大概还有三分之一的表元是空的，所以在快要达到这个阈值的时
  候，原有的散列表会被复制到一个更大的空间里面。这时候重新hash导致排列顺序改变。

  5.由此可知，不要对字典同时进行迭代和修改。如果想扫描并修改一个字典，最好分成
  两步来进行：首先对字典迭代，以得出需要添加的内容，把这些内容放在一个新字典
  里；迭代结束之后再对原有字典进行更新。

参考文献

https://blog.csdn.net/AndrExpert/article/details/77900395
https://www.jianshu.com/p/230e6fde9c75
https://www.cnblogs.com/SmallWZQ/p/8443805.html
https://blog.csdn.net/qq_29287973/article/details/78429209