《算法图解》JavaScript中递归和快排

1.递归

参考文章：https://www.cnblogs.com/YikaJ/p/4263873.html#top

我们先来了解递归：
递归算法，是将问题转化为规模缩小的同类问题的子问题，每一个子问题都用一个同样的算法去解决。一般来说，一个递归算法就是函数调用自身去解决它的子问题。

递归算法的特点：
1.在函数过程中调用自身。
2.在递归过程中，必须有一个明确的条件判断递归的结束，既递归出口。
3.递归算法简洁但效率低，通常不作为推荐算法。

我们通过示例来进一步了解递归使用：

1.阶乘

问题描述： n! = n*(n-1)…21

function fac(n) {
	
	if(n<=1){
		return 1;
	}else{
		return n*fac(n-1);
	}
	
}

我们拿到问题的时候，我们按照定义的说明，可以先将规模缩小到同类的子问题。比如，n! 是等于 n* (n-1)!，然后(n-1)! = (n-1)*(n-2)!。这样依次往下推，直到if的出口。函数实现起来是不是简洁明了呢。当然因为问题规模简单，其实用循环也是可以实现的，大家可以尝试一下。

2.斐波那契数列

问题描述：1, 1, 2, 3, 5, 8, 13, 21, 34, … 求第n个数是多少。

function fib(n){

	if (n <= 0) return 0;
	if (n <= 2) return 1;
	return fib(n-1)+fib(n-2);

}

其实用刚才的想法实现，也是非常的简单的。通过分析可以得到第n个数，是前两个数的和，通过这个我们就可以通过递归，不断获得所需要的前两个数，直到n<= 2这个条件返回1。

3.走楼梯问题

问题描述：楼梯有n阶台阶，上楼可以一步上1阶，也可以一步上2阶或者3阶，计算共有多少种不同的走法。

function stairs(n) {

	//不同方法是指【完成】一件事不同方法
	if(n<=0) return 0;
	if(n==1) return 1;
	if(n==2) return 2;
	if(n==3) return 4;

	return stairs(n-1)+stairs(n-2)+stairs(n-3);
	
}

这其实就是一个斐波那契数列的一种实现。我们分析的时候，可以转化成小规模的子类问题。当到达指定阶梯的最后一步的时候，可以有三种种情况，一是上一步，二是上两步，三是上三步。所以总的方法是F(n) = F(n-1) + F(n-2) + F(n-3)。然后自然就成了各自的小计算，不断循环下去，直到判断条件的发生。

4.最大公约数

问题描述：给两个数，如果两个数相等，最大公约数是其本身。如果不等，取两个数相减的绝对值和两个数中最小的数比较，相等则为最大公约，不等则继续上面的算法，直到相等。

function divissor(a,b){

	if(a === b) return a;
	return divissor(Math.abs(a-b),Math.min(a,b))
	
}

没什么好说的，照问题描述所要求的实现就可以了。递归的出口便在于a等于b。

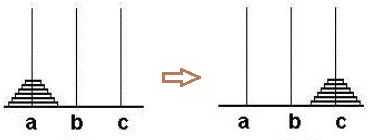
5.汉诺塔

问题描述：汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？

var haoni  = function(){

	if(n > 0){
		haoni(n-1,src,dest,aux);
		console.log("移动第"+ n + "个圆盘从" + src + "到" +dest);
		haoni(n-1,aux,src,dest)
	}

}

haoni(3,"A","B","C")

在我没有体会到递归的精粹前，我对这个问题简直百思不得其解。我一直问自己，我怎么知道下一个该去哪里？后来，我就知道，我其实更关心的是，最后那一个该怎么走。这个怎么说呢？我们可以从头想起，我们如果只有1个盘，我们可以让它到C柱，也可以到B柱。自然两个盘，也可以实现。3个盘，也是可以的吧。那我们就讲4个盘的情况。4个盘要完成就要将A上的圆盘，完全转移到C上。我们把前3个盘当作一个整体放到B上，然后第4个盘就可以到C上了，然后我们再将前三个放到C上，就成功了。那前三个盘，又可以重新当作一个新游戏，让前两个盘，当一个整体，依次类推。这样我们只需要关心大的整体的事，其它的就转成小规模问题解决就好了。

参考文章：https://www.cnblogs.com/antineutrino/p/3334540.html

6.DOM树的递归

问题描述：获取一个节点的所有父节点的tagName

var arr = [];
var getParent = function(node){

	node = node.parentNode;
	if(node.tagName){
		arr.push(node.tagName);
		getParent(node);
	}

}

递归更多可以看：
http://www.cnblogs.com/liu666/p/5745301.html
https://juejin.im/post/59b88ede5188256c60692a85
https://juejin.im/entry/594a48395c497d006b0dfcf6

2.快排

快排是递归经典应用。

function quicksort(arr)
{
    if (arr.length == 0) return [];
    let left = [];
    let right = [];
    let pivot = arr[0];
    for (let i = 1; i < arr.length; i++) {
        if (arr[i] < pivot) {
           left.push(arr[i]);
        } else {
           right.push(arr[i]);
        }
    }
    return quicksort(left).concat(pivot, quicksort(right));
}
console.log(quicksort([2,4,5,49,63,4,5,55,2,4,43])); // [2, 2, 4, 4, 4, 5, 5, 43, 49, 55, 63]

还可以参考文章：http://www.cnblogs.com/YikaJ/p/4129569.html