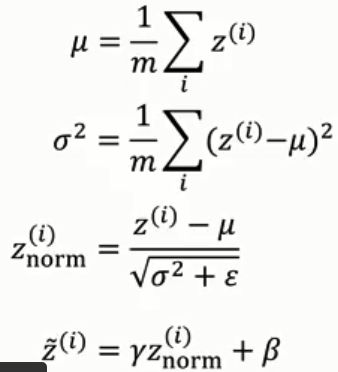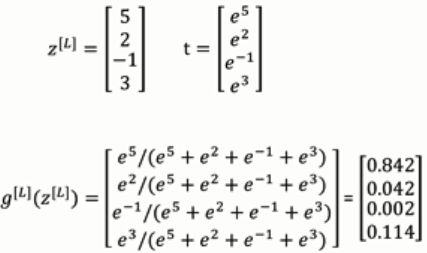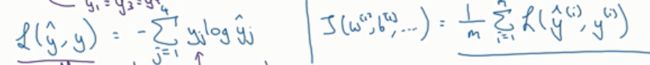https://zhuanlan.zhihu.com/p/29895933
momenta算法：
学习率的衰减：在学习初期 ，学习率较大的时候，步伐大，下降快；但是在将近收敛的时候，学习率变小，这样可以保证在最低点附近浮动。
公式：学习率衰减公式：
超参数：衰减指数decay_rate，a0
其他可以用来做学习率衰减的公式：第三种是离散下降
局部最优问题：
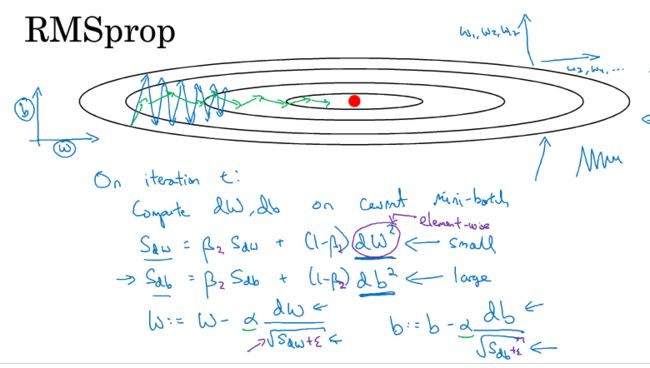
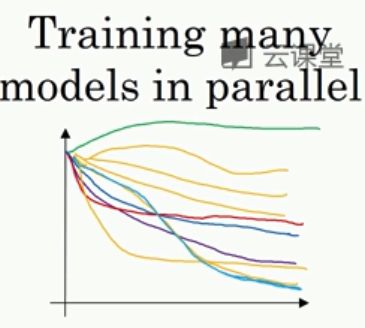
这个图是代价函数的等高图，Adam，RMsprop，mpmenta算法可以快速走过平稳段。
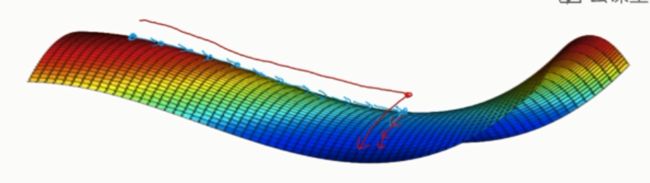
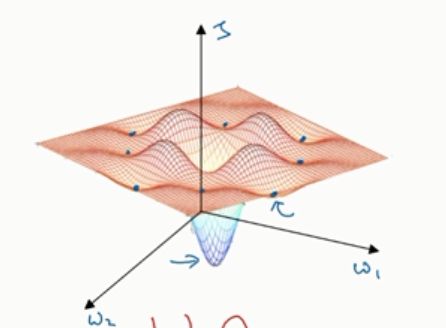
在高纬度的代价函数优化问题中，迭代过程中并不会落入局部最优解，而是会得到一个鞍点，右边的图是代价函数图像，所以这个鞍点是梯度为0，但是却不是局部最小值。
第三周：3.3超参数调试
3.4 3.5 正则化网络激活（batch norm）在拟合深度神经网络的时候让学习得更快
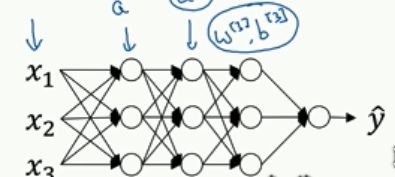
z是一个矢量，每一个分量代表的是l层从上到下的线性相加的结果。
batch norm的公式就是右边的四个，这些式子将数据归一化，然后用r,ß来设置这些数据的均值和方差，r为方差，ß是均值。（这里注意区分momentum里面的ß区分开）
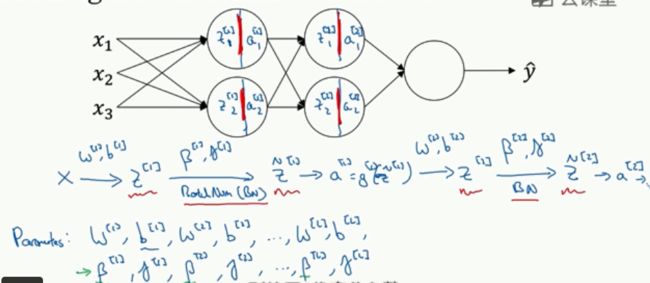在神经元节点之后算出的z进行batch norm得到Zn，再求A，在TensorFlow里面用一句代码就可以：tf.nn.batch-normnalization
bacth norm和minibatch相结合，由于z的均值之后要设置成ß，所以我们在设置wx+b的时候，将b省去，
3.6 原理
batch norm 使得输入值的改变问题，使得输入值得到一定的稳定，这里的输入值是指每一个隐藏层的前一层输出指，batch norm不仅仅是针对神经网络的输入值，还作用于各隐藏层。所以给隐藏层添加了噪音也有一些正则化的作用
3.7 测试时的batch norm
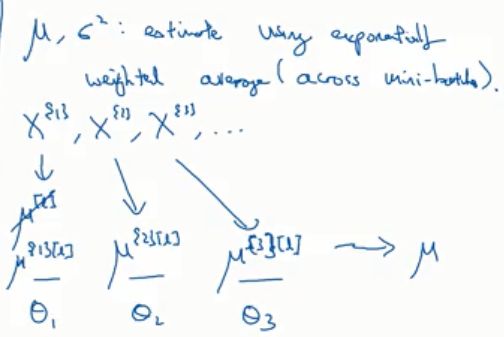
在训练的时候我们得到的batch norm是针对一个个的mini_batch，会有很多个，但是在测试阶段我们没法拿这么多个来用，所以测试使用的batch norm每一层的参数是求之前训练得到的每一层参数的指数加权平均：
3.8 softmax回归
用于m(m>=2)元分类：输出是一个m*1维的向量。
softmax函数的输入是一个m*1的向量输出也是一个m*1向量：softmax要做的就是激活而且归一化使得结果满足概率的性质。
softmax可以直接用来进行一些线性分类决策，加上神经网络的隐藏层之后softmax就可以用来做非线性分类决策。softmax把二类逻辑回归扩展到多类。
hardmax就是把大的数直接映射成1，小的数映射成0 ，而softmax就比较温和。
3.9 -3.10softmax的训练
在神经网络的训练里面不可缺少的是损失函，所以了解新的激活函数之后要注意使用新的损失函数。
最大似然函数作为损失函数（要注意除以M）
：
注意在这种神经网络里面的y是（c,m），其中的c是种类的个数，m是样本数，输出yhat是（c,m）