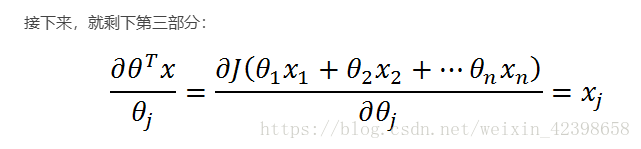机器学习--详解基于梯度下降的Logistic回归算法原理
先给出Logistic回归的sigmod函数数学表达式：
很简单的表达式，再看看它的性质，当
时，
,因此
当
时，
，因此
Logistic回归之所以称为Logistic是因为只有两个状态即0和1，这也是数电中的逻辑数即布尔数，那么为什么需要这样的回归呢？因为针对二分类问题，有两个这样的输出是最好不过了，但是具有逻辑性质还有其他函数，为什么就选择这这个函数呢？
现实中确实存在这样的信号，通信专业的同学都知道有一个信号是阶跃函数，该函数在0这一点瞬间改变到1，但是这个信号的瞬间跳跃很难处理，或者说频率太高而无法处理，而sigmod函数很好的处理了高频特性，他虽不是一瞬间改变状态，但是当数很大时很接近了，同时在0的左右处于非线性区间，这对后面的深度学习的激活函数很有用，今天就不深入讲了，等到后面实战深度学习在好好探讨该函数的其他性质。
实现Logistic回归的分类器，我们可以在每个特征上都乘以一个回归系数，然后所有的结果相加，将这个总和代入上面的sigmod函数中，进而得到0~1的数值，把大于0.5 的数据分为1类，把小于0.5的分为0类，所以Logistic回归也是一种概率估计。
确定好分类器后，剩下的就是找到一组最佳回归系数，这个回归系数如何找 ？这属于优化问题，优化问题，经常使用的是梯度下降算法， 在上篇的博客中，详细的探讨了什么是梯度，为什么梯度总是沿着函数增加的方向，梯度下降又是什么？在上篇博客中详细的解说了，不懂的可以查看我的这篇博客。
我们知道了，所谓梯度其实就是一阶函数的一阶偏导所组成的向量，因此我们只需要求出一阶偏导，代入x，梯度就找到了，但是呢我们的函数是含有未知数的即
，其中【
】是未知数
，有未知数怎么求导，又怎么求该点的梯度呢？这时候就需要我们概率论的方面的知识了即最大释然估计了，这个先不展开讲了，以后自然语言处理还会大量的使用最大释然法，到那里在深入总结，想知道的可以自行学习一下，我直接给出最大释然的推倒工程的公式了：
这个公式学过概率论的想必大家不陌生把，不懂的去百度，搞懂什么是释然估计，有什么用？什么条件下使用，这个在自然语言处理里经常使用的，有时间我单独写一篇释然估计方面的博客。废话不多说了，继续往下：
先解释一下上面的符号意义，如果知道释然估计的同学，应该都能理解所谓的
其实就是我们要求的权值向量了，因为最大释然估计的意义就在于找到一组参数，使得发生的概率最大，例如Logistic回归的分为0或者1的概率最大，那既然已经求得表达式了。此时就可以求梯度了，根据上一篇的梯度理解可知对求偏导就好了：
需要解释一下，下面属于链式求导。
到这里梯度的上升的理论说明就结束了，现在对比一下关键代码进行详解：
h = sigmoid(datamattrix.dot(weights))
error = (labelmat - h)
weights = weights + alpha * (datamattrix.transpose() @ error) 其中error = (labelmat - h)就是上式中的
了，而datamattrix.transpose()就是
了，alpha就是步进系数了，结果很简单，代码也很简单，但是得到这个结果的过程不简单，虽然我们可以不用理解这些过程，但是理解原理会使你走向更高的高度，反之永远是个码农，最可怕的是当你移植别人的代码时，如果你不懂原理，你敢尝试修改代码吗？即使你可以修改代码，但是调优的过程也是很可怕的，因为你没有理解本质的东西，如果原理你懂了，调优就很容易了，另外就是开源代码那么多，我为什么还要写算法呢？不是想使用自己写的代码进行工作，想知道这个算法的实现过程，从理论到实践的转换是如何了，一旦搞明白这些了，以后调优也就知道如何下手了，您说呢？
还需强调一下梯度下降算法，其实主要区别就是加一个负号，这个符号的可以在这个方面体现，这是上升的，即标签值减去预测值为上升，，下降的话，把二者调换位置就可以了。如果以后遇到梯度下降发现别人没添加负号啊，其实隐藏在这个式子里了
至于随机的就不解释了，很简单，不是所有的样本都参与训练，只是抽取一部分进行训练。
下面是机器学习实战手写代码：
#!/usr/bin/env/python
# -*- coding: utf-8 -*-
# Author: 赵守风
# File name: log_regres.py
# Time:2018/10/9
# Email:[email protected]
import numpy as np
# 加载数据使用
def load_data_set():
data_mat = []
label_mat = []
fr = open('testSet.txt') # 数据为（100,3）
for line in fr.readlines():
lines = line.strip().split()
# 把数据转换成列表字符串形式，strip只能删除开头和结尾的字符，默认删除两边的空白符，例如：/n, /r, /t, ' '
# split切片，默认为所有的空字符，包括空格、换行(\n)、制表符(\t)等
data_mat.append([1.0, float(lines[0]), float(lines[1])]) # 此时data的维度还是（100,3）
label_mat.append(int(lines[2])) # 标签维度为1行100列
return data_mat, label_mat
# sigmoid函数
def sigmoid(inx):
return 1.0/(1 + np.exp(- inx))
# 梯度提升算法
def grad_ascent(data_mat_in, class_labels):
datamattrix = np.mat(data_mat_in) # 转换为numpy可以处理的数据类型
labelmat = np.mat(class_labels).transpose() # 100行1列
m,n = np.shape(datamattrix) # 得到数组的维度100,3
print(m, n)
alpha = 0.001
maxcycles = 500
weights = np.ones((n, 1)) # 权值为（3,1）的，初始为1
for k in range(maxcycles):
# 在这里会出错，在python3中的矩阵运算为mat1.dot(mat2)或者是mat1@mat2
h = sigmoid(datamattrix.dot(weights)) # 此时为矩阵计算（100,3）*（3，1）因此会得到（100,1）维度的矩阵
error = (labelmat - h) # 计算差值，这应该是最小二乘法啊？，但是为什么会是梯度，晚点博客详解
weights = weights + alpha * (datamattrix.transpose() @ error) # 矩阵相乘，和上面一样的错误
# 这一句是这段代码最不好理解的，，其实很简单，首先要明确，weights的维度为（3,1），而alpha为数值常数，
# datamattrix的维度为（100,3）的，经过转置以后为（3,100），而error为（100,1）
# 因此datamattrix.transpose() * error的维度就是（3,1）的，从数据意义解释一下，因为error是训练值和真实值
# 的差，此时有100行一列，即每个样本对应一个误差值，然后和原始数据相乘的意义就是梯度了，因为梯度的基本
# 形式为：datamattrix.transpose() * error或者是datamattrix.transpose() * (labelmat - h)
return weights
# 画图
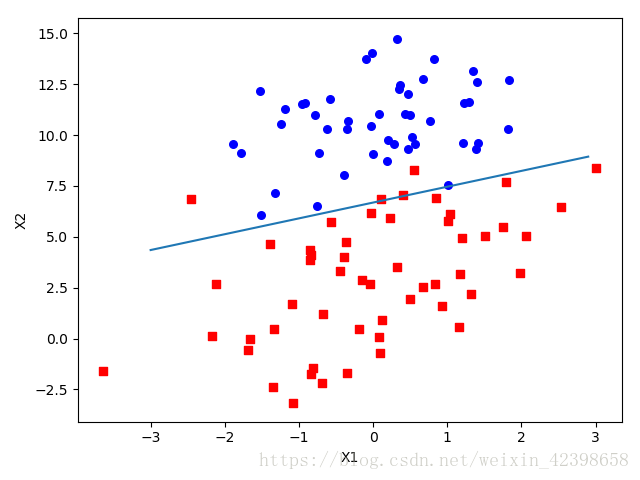
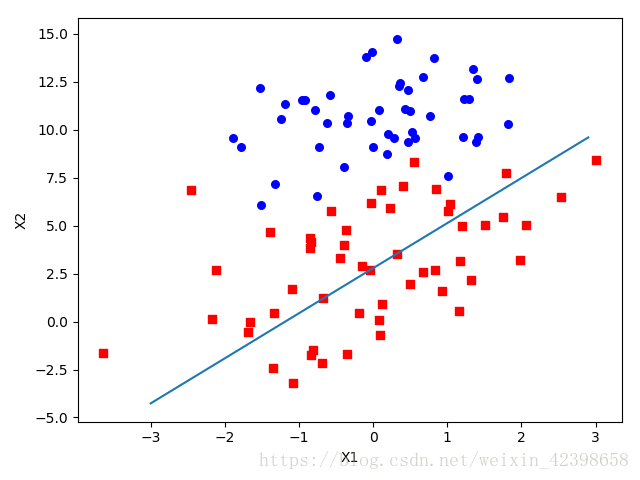
def plotbestfit(weights):
import matplotlib.pyplot as plt
datamat, labelmat = load_data_set()
dataarr = np.array(datamat)
n = np.shape(datamat)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelmat[i]) == 1:
xcord1.append(dataarr[i, 1]);
ycord1.append(dataarr[i, 2])
else:
xcord2.append(dataarr[i, 1]);
ycord2.append(dataarr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='blue')
x = np.arange(-3.0, 3.0, 0.1)
# 画出直线，weights[0]*1.0+weights[1]*x+weights[2]*y=0
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y.transpose()) # 出错，原因是维度不对，需要转置一下
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
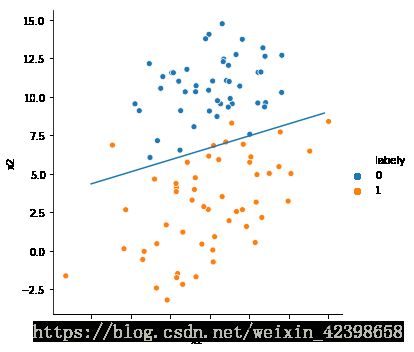
本人不喜欢这种自己画图的风格，需要自己敲代码，我使用另外一种画图工具seaborn画，也是基于matplotlib的更高级的画图接口函数。
data = pd.read_table('testSet.txt', names=['x1','x2','labely']) # 把数据转换成dataframe类型数据，共后面的画图使用
dataarr, labelmat = load_data_set() #调用上面写的读取数据函数，共训练使用
weights = grad_ascent(dataarr, labelmat) # 调用上面的函数，返回权值
sns.relplot(x='x1', y='x2',data=data,hue='labely') # 先画散点图，这里先使用relplot函数进行画，后面使用专门的回归函数作对比
# 和 机器学习实战一样
x = np.arange(-3.0, 3.0, 0.1)
# 画出直线，weights[0]*1.0+weights[1]*x+weights[2]*y=0
y = (-weights[0] - weights[1] * x) / weights[2]
plt.plot(x, y.transpose()) # 把图形添加到图上即可
plt.show()
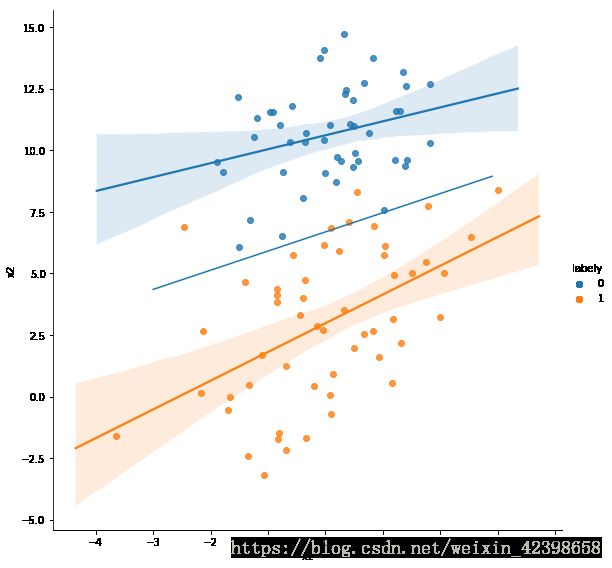
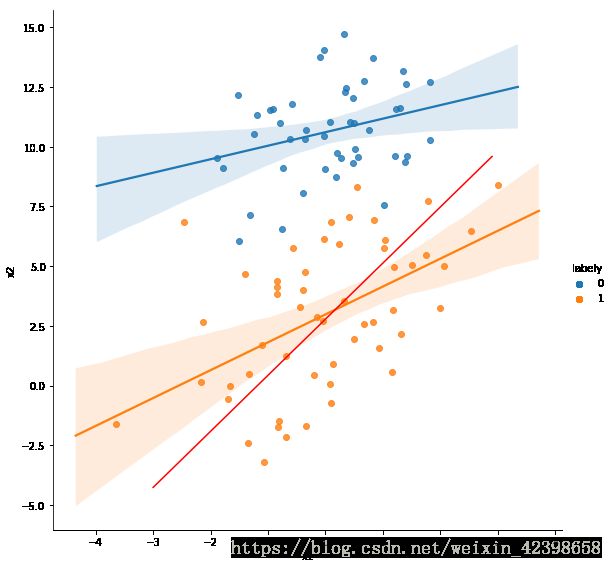
使用seaborn画图自带的回归和使用自己写的对比一下，红色是函数自带的回归，蓝色是自己写的函数的回归
sns.regplot(x='x1', y='x2',data=data,color='red',marker='x')
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
plt.plot(x, y.transpose())
plt.show()
sns.lmplot(x='x1', y='x2',data=data,hue='labely',height=8,)
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
plt.plot(x, y.transpose())
plt.show()
随机梯度上升法：
调试了一个多小时，问题出现在数据类型不一致，首先传进来的数据是list类型，可以查看加载
数据的返回值，而传进来以后呢，定义的weights是numpy数组型的，他们是不同的数据格式，
而且他们肯定不能进行计算处理的，报错千奇百怪，还有就是每次计算只计算一个样本，不是矩阵，
上面那个是矩阵计算，他们的计算方式也不同，需要格外留意
同过这次会加深理解列表、np.narray、pd.Series、pd.Datafram的数据类型的重要区别
# 随机梯度上升算法，即不全部加载数据，而是分批次加载，好处是当数据量很大时，这样做计算量降低
def stoc_gra_ascent0(datamatrix, classlabels):
datamatrix = np.array(datamatrix) # 出错原因相同，类型不匹配
m,n = np.shape(datamatrix)
alpha = 0.01
weights = np.array([1,1,1])
# print('weights', weights)
for i in range(m):
# print('datamatrix[i] * weights = ',datamatrix[i] * weights)
h = sigmoid(np.sum(datamatrix[i] * weights)) # 每次运行一个样本
error = classlabels[i] - h
# print("error : ",error)
weights = weights + alpha * error * datamatrix[i]
return weights
# 调试了一个多小时，问题出现在数据类型不一致，首先传进来的数据是list类型，可以查看加载
# 数据的返回值，而传进来以后呢，定义的weights是numpy数组型的，他们是不同的数据格式，
# 而且他们肯定不能进行计算处理的，报错千奇百怪，还有就是每次计算只计算一个样本，不是矩阵，
# 上面那个是矩阵计算，他们的计算方式也不同，需要格外留意
# 同过这次会加深理解列表、np.narray、pd.Series、pd.Datafram的数据类型的重要区别
sns.lmplot(x='x1', y='x2',data=data,hue='labely',height=8,)
weights = stoc_gra_ascent0(dataarr, labelmat)
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
plt.plot(x, y.transpose(),color='red')
plt.show()
回归系数对比
def stoc_gra_ascent0(datamatrix, classlabels):
datamatrix = np.array(datamatrix) # 出错原因相同，类型不匹配
m,n = np.shape(datamatrix)
alpha = 0.01
weights = np.array([1,1,1])
weights_temp = []
i_temp = []
for j in range(5): # 增加迭代次数，后面就是通过这里进行增加迭代次数的，现在次数为5*m = 5*100 =500次
for i in range(m):
h = sigmoid(np.sum(datamatrix[i] * weights)) # 每次运行一个样本
error = classlabels[i] - h
weights = weights + alpha * error * datamatrix[i]
# 收集权值变化信息，和迭代次数
weights_temp.append(weights)
i_temp.append(j*m+i)
return weights, weights_temp, i_temp
调用函数 打印信息
dataarr, labelmat = log_regres.load_data_set()
weights , weights_temp ,i_temp= log_regres.stoc_gra_ascent0(dataarr, labelmat)
data = pd.DataFrame(weights_temp, columns=['x0','x1','x2']) # 把数据转化为pandas格式
data['i'] = i_temp # 把迭代次数也添加进去，目的是容易画图呀，不加进去还有写for循环
print(data.head()) # 看前5行数据
# 下面三句是画回归图的
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
log_regres.plotbestfit(weights)
# 下面是画权值变化图的
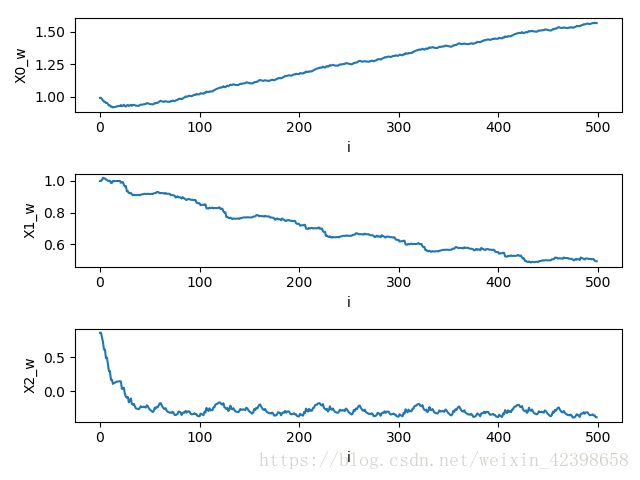
plt.subplot(3, 1, 1)
plt.plot(data['i'], data['x0'])
plt.xlabel('i')
plt.ylabel('X0_w')
plt.subplot(3, 1, 2)
plt.plot(data['i'], data['x1'])
plt.xlabel('i')
plt.ylabel('X1_w')
plt.subplot(3, 1, 3)
plt.plot(data['i'], data['x2'])
plt.xlabel('i')
plt.ylabel('X2_w')
plt.show()
print(data.head()) # 看前5行数据 x0 x1 x2 i
0 0.990000 1.000176 0.859469 0
1 0.990266 0.999805 0.860708 1
2 0.980294 1.007306 0.795506 2
3 0.970342 1.020466 0.724320 3
4 0.960342 1.016233 0.613782 4
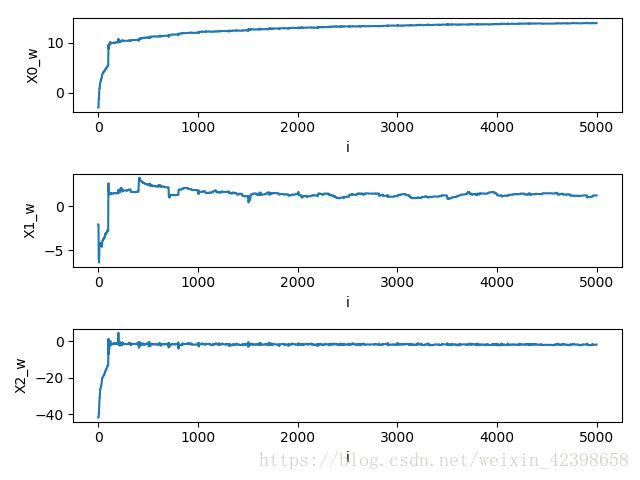
迭代次数增加到5000次：
从增加迭代次数发现，迭代次数越多，分类越准确，同时权值趋于稳定。大家可以试试多迭代几次看看。
改进的随机梯度上升算法
# 改进梯度上升算法
def stoc_gra_ascent1(datamatrix, classlabels, numiter=50):
datamatrix = np.array(datamatrix) # 出错原因相同，类型不匹配
m,n = np.shape(datamatrix)
alpha = 0.01
weights = np.array([1,1,1])
weights_temp = []
i_temp = []
for j in range(numiter):
dataindex = range(m) # 获取数据的索引范围
for i in range(m):
alpha = 4/(1.0+j+i)+0.01 # 随着迭代次数的增加，alpha的值也会改变，且不是线性下降的，同时该参数
# 不会降低为0，这样可以很好的处理系数波动
randindex = int(np.random.uniform(0,len(dataindex)))
# 获取索引范围内的任意一个值
h = sigmoid(np.sum(datamatrix[randindex] * weights)) # 每次运行一个样本，这个样本是上面代码随机选取到的
error = classlabels[randindex] - h
weights = weights + alpha * error * datamatrix[randindex]
# 收集权值变化信息，和迭代次数
weights_temp.append(weights)
i_temp.append(j*m+i)
del(list(dataindex)[randindex]) # 删除这使用的值
# TypeError: 'range' object doesn't support item deletion出错，原因是需要强制类型转换
return weights, weights_temp, i_temp
# 调用画图
dataarr, labelmat = log_regres.load_data_set()
weights , weights_temp ,i_temp= log_regres.stoc_gra_ascent1(dataarr, labelmat)
data = pd.DataFrame(weights_temp, columns=['x0','x1','x2']) # 把数据转化为pandas格式
data['i'] = i_temp # 把迭代次数也添加进去，目的是容易画图呀，不加进去还有写for循环
print(data.head()) # 看前5行数据
# 下面三句是画回归图的
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
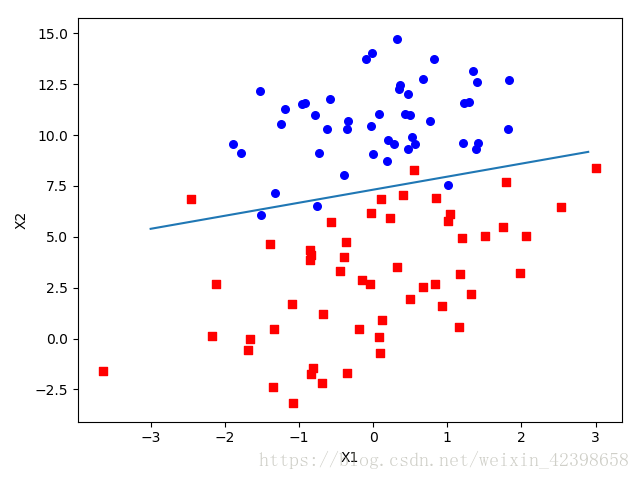
log_regres.plotbestfit(weights)
# 下面是画权值变化图的
plt.subplot(3, 1, 1)
plt.plot(data['i'], data['x0'])
plt.xlabel('i')
plt.ylabel('X0_w')
plt.subplot(3, 1, 2)
plt.plot(data['i'], data['x1'])
plt.xlabel('i')
plt.ylabel('X1_w')
plt.subplot(3, 1, 3)
plt.plot(data['i'], data['x2'])
plt.xlabel('i')
plt.ylabel('X2_w')
plt.show()
正确率明显提升了，seaborn就不画了，和前面差不多，有兴趣的同学可以多画画
下面给出机器学习实战的示例：从疝气病症预测病马死亡率
import numpy as np
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
h_data_train = pd.read_table('horse-colic.data.txt',sep='\s+',header=None, na_values=['NULL']) # 载入原始数据
# 可以到这个网站下载原始数据https://archive.ics.uci.edu/ml/datasets/Horse+Colic
h_data_train.shape # 查看数据维度，该数据维度为(300, 28)，即300个数据，28个特征
h_data_train = h_data_train.replace('?',np.nan) # 把空缺值使用nan代替
h_data_train.head()# 查看数据
0 1 2 3 4 5 6 7 8 9 ... 18 19 20 21 22 23 24 25 26 27
0 2 1 530101 38.50 66 28 3 3 NaN 2 ... 45.00 8.40 NaN NaN 2 2 11300 0 0 2
1 1 1 534817 39.2 88 20 NaN NaN 4 1 ... 50 85 2 2 3 2 2208 0 0 2
2 2 1 530334 38.30 40 24 1 1 3 1 ... 33.00 6.70 NaN NaN 1 2 0 0 0 1
3 1 9 5290409 39.10 164 84 4 1 6 2 ... 48.00 7.20 3 5.30 2 1 2208 0 0 1
4 2 1 530255 37.30 104 35 NaN NaN 6 2 ... 74.00 7.40 NaN NaN 2 2 4300 0 0 2
5 rows × 28 columns
horse_colic_train = h_data_train.fillna(0) # 把空缺值使用0值填充
data = horse_colic_train.dropna() # 把还没有处理完的空缺值剔除
data.head()
0 1 2 3 4 5 6 7 8 9 ... 18 19 20 21 22 23 24 25 26 27
0 2 1 530101 38.50 66 28 3 3 0 2 ... 45.00 8.40 0 0 2 2 11300 0 0 2
1 1 1 534817 39.2 88 20 0 0 4 1 ... 50 85 2 2 3 2 2208 0 0 2
2 2 1 530334 38.30 40 24 1 1 3 1 ... 33.00 6.70 0 0 1 2 0 0 0 1
3 1 9 5290409 39.10 164 84 4 1 6 2 ... 48.00 7.20 3 5.30 2 1 2208 0 0 1
4 2 1 530255 37.30 104 35 0 0 6 2 ... 74.00 7.40 0 0 2 2 4300 0 0 2
5 rows × 28 columns
data.shape # 在查看数据维度为(300, 28)
data.to_csv('horse_train.csv') # 导出数据，可以是txt，使用data.to_table（）即可
上面处理的是训练数据，测试数据也是一样的，不过作者的数据只有22个特征，不知道去掉了哪些特征，也没去仔细分析，所以下面使用的还是作者处理好的数据，如果知道哪些特征，处理他们还是很简单的
数据预处理就结束了，下面给出测试代码，但是需要说明的几处就是，不能照搬上面的代码，需要修改一下代码，因为上面代码我插入了画权值的图形的数据代码，需要修改一下，大家务必小心，错误基本上是维度不对，相信的大家应该可以解决。
#!/usr/bin/env/python
# -*- coding: utf-8 -*-
# Author: 赵守风
# File name: log_regres.py
# Time:2018/10/9
# Email:[email protected]
import numpy as np
import matplotlib.pyplot as plt
# 加载数据使用
def load_data_set():
data_mat = []
label_mat = []
fr = open('testSet.txt') # 数据为（100,3）
for line in fr.readlines():
lines = line.strip().split()
# 把数据转换成列表字符串形式，strip只能删除开头和结尾的字符，默认删除两边的空白符，例如：/n, /r, /t, ' '
# split切片，默认为所有的空字符，包括空格、换行(\n)、制表符(\t)等
data_mat.append([1.0, float(lines[0]), float(lines[1])]) # 此时data的维度还是（100,3）
label_mat.append(int(lines[2])) # 标签维度为1行100列
return data_mat, label_mat
# sigmoid函数
def sigmoid(inx):
return 1.0/(1 + np.exp(- inx))
# 梯度提升算法
def grad_ascent(data_mat_in, class_labels):
datamattrix = np.mat(data_mat_in) # 转换为numpy可以处理的数据类型
labelmat = np.mat(class_labels).transpose() # 100行1列
m,n = np.shape(datamattrix) # 得到数组的维度100,3
print(m, n)
alpha = 0.001
maxcycles = 500
weights = np.ones((n, 1)) # 权值为（3,1）的，初始为1
for k in range(maxcycles):
# 在这里会出错，在python3中的矩阵运算为mat1.dot(mat2)或者是mat1@mat2
h = sigmoid(datamattrix.dot(weights)) # 此时为矩阵计算（100,3）*（3，1）因此会得到（100,1）维度的矩阵
error = (labelmat - h) # 计算差值，这应该是最小二乘法啊？，但是为什么会是梯度，晚点博客详解
weights = weights + alpha * (datamattrix.transpose() @ error) # 矩阵相乘，和上面一样的错误
# 这一句是这段代码最不好理解的，，其实很简单，首先要明确，weights的维度为（3,1），而alpha为数值常数，
# datamattrix的维度为（100,3）的，经过转置以后为（3,100），而error为（100,1）
# 因此datamattrix.transpose() * error的维度就是（3,1）的，从数据意义解释一下，因为error是训练值和真实值
# 的差，此时有100行一列，即每个样本对应一个误差值，然后和原始数据相乘的意义就是梯度了，因为梯度的基本
# 形式为：datamattrix.transpose() * error或者是datamattrix.transpose() * (labelmat - h)
return weights
def plotbestfit(weights):
import matplotlib.pyplot as plt
datamat, labelmat = load_data_set()
dataarr = np.array(datamat)
n = np.shape(datamat)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelmat[i]) == 1:
xcord1.append(dataarr[i, 1]);
ycord1.append(dataarr[i, 2])
else:
xcord2.append(dataarr[i, 1]);
ycord2.append(dataarr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='blue')
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y.transpose()) # 出错，原因是维度不对，需要转置一下
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
# 随机梯度上升算法，即不全部加载数据，而是分批次加载，好处是当数据量很大时，这样做计算量降低
def stoc_gra_ascent0(datamatrix, classlabels):
datamatrix = np.array(datamatrix) # 出错原因相同，类型不匹配
m,n = np.shape(datamatrix)
alpha = 0.01
weights = np.array([1,1,1])
weights_temp = []
i_temp = []
for j in range(200):
for i in range(m):
h = sigmoid(np.sum(datamatrix[i] * weights)) # 每次运行一个样本
error = classlabels[i] - h
weights = weights + alpha * error * datamatrix[i]
# 收集权值变化信息，和迭代次数
weights_temp.append(weights)
i_temp.append(j)
return weights, weights_temp, i_temp
# 调试了一个多小时，问题出现在数据类型不一致，首先传进来的数据是list类型，可以查看加载
# 数据的返回值，而传进来以后呢，定义的weights是numpy数组型的，他们是不同的数据格式，
# 而且他们肯定不能进行计算处理的，报错千奇百怪，还有就是每次计算只计算一个样本，不是矩阵，
# 上面那个是矩阵计算，他们的计算方式也不同，需要格外留意
# 同过这次会加深理解列表、np.narray、pd.Series、pd.Datafram的数据类型的重要区别
# 改进梯度上升算法
def stoc_gra_ascent1(datamatrix, classlabels, numiter=50):
datamatrix = np.array(datamatrix) # 出错原因相同，类型不匹配
m,n = np.shape(datamatrix)
alpha = 0.01
weights = np.ones(n)
weights_temp = []
i_temp = []
for j in range(numiter):
dataindex = range(m) # 获取数据的索引范围
for i in range(m):
alpha = 4/(1.0+j+i)+0.01 # 随着迭代次数的增加，alpha的值也会改变，且不是线性下降的，同时该参数
# 不会降低为0，这样可以很好的处理系数波动
randindex = int(np.random.uniform(0,len(dataindex)))
# 获取索引范围内的任意一个值
h = sigmoid(np.sum(datamatrix[randindex] * weights)) # 每次运行一个样本，这个样本是上面代码随机选取到的
error = classlabels[randindex] - h
weights = weights + alpha * error * datamatrix[randindex]
# 收集权值变化信息，和迭代次数
weights_temp.append(weights)
i_temp.append(j*m+i)
del(list(dataindex)[randindex]) # 删除这使用的值
# TypeError: 'range' object doesn't support item deletion出错，原因是需要强制类型转换
return weights, weights_temp, i_temp
# return weights # 需要修改，原因是从疝气病症预测病马死亡率调用会出错，
#------------------------------从疝气病症预测病马死亡率------------------------------------------------#
# sigmod判断
def classifyvector(inx, weights):
prob = sigmoid(sum(inx * weights))
if prob > 0.5:
return 1.0
else:
return 0
def colic_test():
fr_train = open('horseColicTraining.txt')
fr_test = open('horseColicTest.txt')
training_set = []
training_labels = []
for line in fr_train.readlines():
currline = line.strip().split('\t')
linearr = []
for i in range(21):
linearr.append(float(currline[i]))
training_set.append(linearr)
training_labels.append(float(currline[21]))
train_weights, weights_temp, i_temp = stoc_gra_ascent1(np.array(training_set), np.array(training_labels), 500) # 前面为了画图返回的参数
errorcount = 0
numtestvec = 0.0
for line in fr_test.readlines():
numtestvec += 1.0
linearr = []
currline = line.strip().split('\t')
for i in range(21):
linearr.append(float(currline[i]))
if int(classifyvector(np.array(linearr), np.array(train_weights))) != int(currline[21]): # 出错
errorcount += 1.0
errorrate = (float(errorcount) / numtestvec)
print('错误率为： ', errorrate)
return errorrate,weights_temp, i_temp
def multitest():
numtests = 10
errorsum = 0.0
for k in range(numtests):
errorrate_tep, weights_temp, i_temp = colic_test()
errorsum += errorrate_tep
print('%d 次迭代后，平均错误率为： %f' % (numtests, errorsum/float(numtests)))
上面是整个可执行的代码，在jupyter notebook可运行。
multitest()执行该函数后输出结果为：
错误率为： 0.2537313432835821
错误率为： 0.31343283582089554
错误率为： 0.3880597014925373
错误率为： 0.26865671641791045
错误率为： 0.2537313432835821
错误率为： 0.34328358208955223
错误率为： 0.3283582089552239
错误率为： 0.23880597014925373
错误率为： 0.2537313432835821
错误率为： 0.26865671641791045
10 次迭代后，平均错误率为： 0.291045大家可以尝试把图画出来。