快速幂算法详解&&快速幂取模算法详解
导语
快速幂算法和快速幂取模算法是重要的算法,与数论有关,本文试图通过阐释两个算法的需求、思想并加以编程实现来帮助读者理解这两个算法。
如能理解,我的荣幸;反之,向您致以真诚的歉意。
本文算法的编程实现基于Java语言。我才不会告诉你文末有彩蛋的呢!
为什么需要快速幂算法
众所周知,指数的朴素求法是这样的:
比如我们求105,就是等价于求解10 * 10 * 10 * 10 * 10,五连乘。
朴素算法的代码如下:
private static long pow1(int a, int b) {
long result = 1;
while (b > 0) {
b--;
result *= a;
}
return result;
}
对于ab的求解,时间复杂度为O(b),即线性的。
但这种效率在某些情况下可能是不够的,这就有了快速幂算法。
什么是快速幂算法
顾名思义,快速幂就是快速算底数a的n次幂(即an)的算法。
其时间复杂度是O(logn),效率比朴素算法大大提高。
看,下图就是大致的对数曲线和线性的比较,可见对数比起线性是好的太多啦:
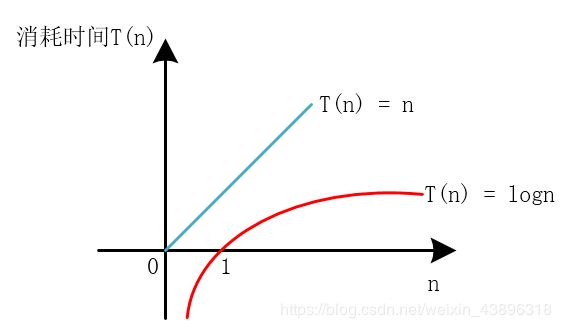
解析快速幂算法
对于ab,指数b是可以拆成二进制的,根据am+n=aman,我们就可以据此拆分ab了。
a13为例,1310=11012,a13自然就得到了表示,最终会转化成a1+a4+a8。
……
快速幂算法代码实现
private static long pow2(int a, int b) {
long result = 1, base = a;
while(b != 0) {
if(b % 2 != 0) {
result *= base;
}
base *= base;
b /= 2;
}
return result;
}
快速幂算法递归版本
private static long recursivePow(int a, int b) {
if(b == 1) {
return a;
}
long temp = recursivePow(a, b/2);
return (b % 2 == 0 ? 1 : a) * temp * temp;
}
快速幂算法位运算版本
位运算没啥别的优点,但快啊~~
- &运算:通常用于二进制取位操作,例如一个数b & 1 的结果就是取二进制的最末位的值。还可以判断这个数的奇偶性,如果b & 1 == 0,则x为偶数;如果b & 1 == 1,则x为奇数。
这种判法比用b % 2要高效. - >>运算:在这里是作为除法来使用,例如一个数b,b >>= 1就表示b右移一位,相当于除以2。
这种判法比b /= 2要高效。
private static long pow3(int a, int b) {
if(b == 0) {
return 1;
}
while((b & 1) == 0) {
b >>= 1;
a *= a;
}
long result = a;
b >>= 1;
while(b != 0){
a *= a;
if((b & 1) != 0) {
result *= a;
}
b >>= 1;
}
return result;
}
快速幂取模算法说明
离散数学的数论部分,有这样一个引理:积的取余等于取余的积的取余。
翻译过来就是:
(AB)modC = [(AmodC)(BmodC)]modC
基于此条引理,对指数型数据进行拆分以及合并,即得到我们所需要的快速幂取模算法。
快速幂取模算法优点
优点不仅仅是快速,更重要的是不要直接把AB求出来,有时候AB很大,乘积会爆掉long(C里的longlong),但取模结果显然不会爆,这就要求我们使用快速幂取模算法,不断减小A和B的规模,从而求解。
因此,拆指数就显得十分重要,这方面可以参考上面的算法啦。
快速幂取模算法简单推导
快速幂取模算法代码实现
private static long quickMode(int a,int b,int c) {
long result = 1;
long temp = a % c;
while(b != 0) {
if((b & 1) != 0) {
result = ( result * temp ) % c;
}
b >>= 1;
temp = (temp * temp) % c;
}
return result;
}
本文完整代码实现(Java语言描述)
import java.math.BigInteger;
public class QuickPower {
private static long pow1(int a, int b) {
long result = 1;
while (b != 0) {
b--;
result *= a;
}
return result;
}
private static long pow2(int a, int b) {
long result = 1, base = a;
while(b != 0) {
if(b % 2 != 0) {
result *= base;
}
base *= base;
b /= 2;
}
return result;
}
private static long recursivePow(int a, int b) {
if(b == 1) {
return a;
}
long temp = recursivePow(a,b/2);
return (b % 2 == 0 ? 1 : a) * temp * temp;
}
private static long pow3(int a, int b) {
if(b == 0) {
return 1;
}
while((b & 1) == 0) {
b >>= 1;
a *= a;
}
long result = a;
b >>= 1;
while(b != 0){
a *= a;
if((b & 1) != 0) {
result *= a;
}
b >>= 1;
}
return result;
}
private static long quickPower(long a, long b) {
long result = 1, temp = a;
while(b != 0) {
if((b & 1) != 0) {
result *= temp;
}
temp *= temp;
b >>= 1;
}
return result;
}
private static long quick(int a,int b,int c) {
long result = 1;
long temp = a % c;
while(b != 0) {
if((b & 1) != 0) {
result = ( result * temp ) % c;
}
b >>= 1;
temp = (temp * temp) % c;
}
return result;
}
}
彩蛋
恭喜你,看到了这里,这里有彩蛋。
还是那句话,练算法归练算法,你也不是打算法竞赛的,平时有时候可以调用Java的API啊,那自然是BigInteger啦:
求幂的方法:
public BigInteger pow(int exponent)
求幂模的方法:
public BigInteger modPow(BigInteger exponent, BigInteger m)
由于BigInteger不是工具类,所以这些不是static的,需要以一个BigInteger对象作为底使用,所以,很方便。
BigInteger这东西,开始用肯定不顺手,但是你慢慢体会它的美,就觉得还是很强的。(尽管运算符在BigInteger身上已经不起作用了)
如有错误,还望指正,不喜勿喷,谢谢您的阅读Orz……
